2. The Standard C++ Library▲
2-0. Introduction▲
Standard C++ not only incorporates all the Standard C libraries (with small additions and changes to support type safety), it also adds libraries of its own. These libraries are far more powerful than those in Standard C; the leverage you get from them is analogous to the leverage you get from changing from C to C++.
This section of the book gives you an in-depth introduction to key portions of the Standard C++ library.
The most complete and also the most obscure reference to the full libraries is the Standard itself. Bjarne Stroustrup's The C++ Programming Language, Third Edition (Addison Wesley, 2000) remains a reliable reference for both the language and the library. The most celebrated library-only reference is The C++ Standard Library: A Tutorial and Reference, by Nicolai Josuttis (Addison Wesley, 1999). The goal of the chapters in this part of the book is to provide you with an encyclopedia of descriptions and examples so that you'll have a good starting point for solving any problem that requires the use of the Standard libraries. However, some techniques and topics are rarely used and are not covered here. If you can't find it in these chapters, reach for the other two books; this book is not intended to replace those books but rather to complement them. In particular, we hope that after going through the material in the following chapters you'll have a much easier time understanding those books.
You will notice that these chapters do not contain exhaustive documentation describing every function and class in the Standard C++ library. We've left the full descriptions to others; in particular to P.J. Plauger's Dinkumware C/C++ Library Reference at http://www.dinkumware.com. This is an excellent online source of standard library documentation in HTML format that you can keep resident on your computer and view with a Web browser whenever you need to look something up. You can view this online or purchase it for local viewing. It contains complete reference pages for the both the C and C++ libraries (so it's good to use for all your Standard C/C++ programming questions). Electronic documentation is effective not only because you can always have it with you, but also because you can do an electronic search.
When you're actively programming, these resources should satisfy your reference needs (and you can use them to look up anything in this chapter that isn't clear to you). Appendix A lists additional references.
The first chapter in this section introduces the Standard C++ string class, which is a powerful tool that simplifies most of the text-processing chores you might have. Chances are, anything you've done to character strings with lines of code in C can be done with a member function call in the string class.
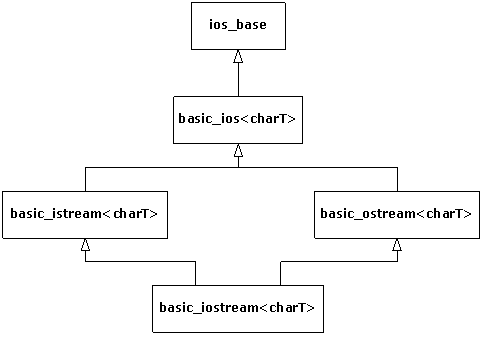
Chapter 4 covers the iostreams library, which contains classes for processing input and output with files, string targets, and the system console.
Although Chapter 5, “Templates in Depth,” is not explicitly a library chapter, it is necessary preparation for the two chapters that follow. In Chapter 6 we examine the generic algorithms offered by the Standard C++ library. Because they are implemented with templates, these algorithms can be applied to any sequence of objects. Chapter 7 covers the standard containers and their associated iterators. We cover algorithms first because they can be fully explored by using only arrays and the vector container (which we have been using since early in Volume 1). It is also natural to use the standard algorithms in connection with containers, so it's good to be familiar with the algorithms before studying the containers.
2-1. Strings in Depth▲
String processing with character arrays is one of the biggest time-wasters in C. Character arrays require the programmer to keep track of the difference between static quoted strings and arrays created on the stack and the heap, and the fact that sometimes you're passing around a char* and sometimes you must copy the whole array.
Especially because string manipulation is so common, character arrays are a great source of misunderstandings and bugs. Despite this, creating string classes remained a common exercise for beginning C++ programmers for many years. The Standard C++ library string class solves the problem of character array manipulation once and for all, keeping track of memory even during assignments and copy-constructions. You simply don't need to think about it.
This chapter(31) examines the Standard C++ string class, beginning with a look at what constitutes a C++ string and how the C++ version differs from a traditional C character array. You'll learn about operations and manipulations using string objects, and you'll see how C++ strings accommodate variation in character sets and string data conversion.
Handling text is one of the oldest programming applications, so it's not surprising that the C++ string draws heavily on the ideas and terminology that have long been used in C and other languages. As you begin to acquaint yourself with C++ strings, this fact should be reassuring. No matter which programming idiom you choose, there are three common things you want to do with a string:
- Create or modify the sequence of characters stored in the string.
- Detect the presence or absence of elements within the string.
- Translate between various schemes for representing string characters.
You'll see how each of these jobs is accomplished using C++ string objects.
2-1-1. What's in a string?▲
In C, a string is simply an array of characters that always includes a binary zero (often called the null terminator) as its final array element. There are significant differences between C++ strings and their C progenitors. First, and most important, C++ strings hide the physical representation of the sequence of characters they contain. You don't need to be concerned about array dimensions or null terminators. A string also contains certain “housekeeping” information about the size and storage location of its data. Specifically, a C++ string object knows its starting location in memory, its content, its length in characters, and the length in characters to which it can grow before the string object must resize its internal data buffer. C++ strings thus greatly reduce the likelihood of making three of the most common and destructive C programming errors: overwriting array bounds, trying to access arrays through uninitialized or incorrectly valued pointers, and leaving pointers “dangling” after an array ceases to occupy the storage that was once allocated to it.
The exact implementation of memory layout for the string class is not defined by the C++ Standard. This architecture is intended to be flexible enough to allow differing implementations by compiler vendors, yet guarantee predictable behavior for users. In particular, the exact conditions under which storage is allocated to hold data for a string object are not defined. String allocation rules were formulated to allow but not require a reference-counted implementation, but whether or not the implementation uses reference counting, the semantics must be the same. To put this a bit differently, in C, every char array occupies a unique physical region of memory. In C++, individual string objects may or may not occupy unique physical regions of memory, but if reference counting avoids storing duplicate copies of data, the individual objects must look and act as though they exclusively own unique regions of storage. For example:
//: C03:StringStorage.h
#ifndef STRINGSTORAGE_H
#define STRINGSTORAGE_H
#include <iostream>
#include <string>
#include "../TestSuite/Test.h"
using std::cout;
using std::endl;
using std::string;
class StringStorageTest : public TestSuite::Test {
public:
void run() {
string s1("12345");
// This may copy the first to the second or
// use reference counting to simulate a copy:
string s2 = s1;
test_(s1 == s2);
// Either way, this statement must ONLY modify s1:
s1[0] = '6';
cout << "s1 = " << s1
<< endl; // 62345
cout << "s2 = " << s2
<< endl; // 12345
test_(s1 != s2);
}
};
#endif //
STRINGSTORAGE_H ///:~//: C03:StringStorage.cpp
//{L} ../TestSuite/Test
#include "StringStorage.h"
int main() {
StringStorageTest t;
t.run();
return t.report();
} ///:~We say that an implementation that only makes unique copies when a string is modified uses a copy-on-write strategy. This approach saves time and space when strings are used only as value parameters or in other read-only situations.
Whether a library implementation uses reference counting or not should be transparent to users of the string class. Unfortunately, this is not always the case. In multithreaded programs, it is practically impossible to use a reference-counting implementation safely.(32)
2-1-2. Creating and initializing C++ strings▲
Creating and initializing strings is a straightforward proposition and fairly flexible. In the SmallString.cpp example below, the first string, imBlank, is declared but contains no initial value. Unlike a C char array, which would contain a random and meaningless bit pattern until initialization, imBlank does contain meaningful information. This string object is initialized to hold “no characters” and can properly report its zero length and absence of data elements using class member functions.
The next string, heyMom, is initialized by the literal argument “Where are my socks?” This form of initialization uses a quoted character array as a parameter to the string constructor. By contrast, standardReply is simply initialized with an assignment. The last string of the group, useThisOneAgain, is initialized using an existing C++ string object. Put another way, this example illustrates that string objects let you do the following:
- Create an empty string and defer initializing it with character data.
- Initialize a string by passing a literal, quoted character array as an argument to the constructor.
- Initialize a string using the equal sign (=).
- Use one string to initialize another.
//: C03:SmallString.cpp
#include <string>
using namespace std;
int main() {
string imBlank;
string heyMom("Where are my socks?");
string standardReply = "Beamed into deep "
"space on wide angle dispersion?";
string useThisOneAgain(standardReply);
} ///:~These are the simplest forms of string initialization, but variations offer more flexibility and control. You can do the following:
- Use a portion of either a C char array or a C++ string.
- Combine different sources of initialization data using operator+.
- Use the string object's substr( ) member function to create a substring.
Here's a program that illustrates these features:
//: C03:SmallString2.cpp
#include <string>
#include <iostream>
using namespace std;
int main() {
string s1("What is the sound of one clam
napping?");
string s2("Anything worth doing is worth
overdoing.");
string s3("I saw Elvis in a UFO");
// Copy the first 8 chars:
string s4(s1, 0, 8);
cout << s4 << endl;
// Copy 6 chars from the middle of the source:
string s5(s2, 15, 6);
cout << s5 << endl;
// Copy from middle to end:
string s6(s3, 6, 15);
cout << s6 << endl;
// Copy many different things:
string quoteMe = s4 + "that" +
// substr() copies 10 chars at element 20
s1.substr(20, 10) + s5 +
// substr() copies up to either 100 char
// or eos starting at element 5
"with" + s3.substr(5, 100) +
// OK to copy a single char this way
s1.substr(37, 1);
cout << quoteMe << endl;
} ///:~The string member function substr( ) takes a starting position as its first argument and the number of characters to select as the second argument. Both arguments have default values. If you say substr( ) with an empty argument list, you produce a copy of the entire string, so this is a convenient way to duplicate a string.
Here's the output from the program:
What is
doing
Elvis in a UFO
What is that one clam doing
with Elvis in a UFO?Notice the final line of the example. C++ allows string initialization techniques to be mixed in a single statement, a flexible and convenient feature. Also notice that the last initializer copies just one character from the source string.
Another slightly more subtle initialization technique involves the use of the string iterators string::begin( ) and string::end( ). This technique treats a string like a container object (which you've seen primarily in the form of vector so far—you'll see many more containers in Chapter 7), which uses iterators to indicate the start and end of a sequence of characters. In this way you can hand a string constructor two iterators, and it copies from one to the other into the new string:
//: C03:StringIterators.cpp
#include <string>
#include <iostream>
#include <cassert>
using namespace std;
int main() {
string source("xxx");
string s(source.begin(), source.end());
assert(s == source);
} ///:~The iterators are not restricted to begin( ) and end( ); you can increment, decrement, and add integer offsets to them, allowing you to extract a subset of characters from the source string.
C++ strings may not be initialized with single characters or with ASCII or other integer values. You can initialize a string with a number of copies of a single character, however:
//: C03:UhOh.cpp
#include <string>
#include <cassert>
using namespace std;
int main() {
// Error: no single char inits
//! string nothingDoing1('a');
// Error: no integer inits
//! string nothingDoing2(0x37);
// The following is legal:
string okay(5, 'a');
assert(okay == string("aaaaa"));
} ///:~The first argument indicates the number of copies of the second argument to place in the string. The second argument can only be a single char, not a char array.
2-1-3. Operating on strings▲
If you've programmed in C, you are accustomed to the family of functions that write, search, modify, and copy char arrays. There are two unfortunate aspects of the Standard C library functions for handling char arrays. First, there are two loosely organized families of them: the “plain” group, and the ones that require you to supply a count of the number of characters to be considered in the operation at hand. The roster of functions in the C char array library shocks the unsuspecting user with a long list of cryptic, mostly unpronounceable names. Although the type and number of arguments to the functions are somewhat consistent, to use them properly you must be attentive to details of function naming and parameter passing.
The second inherent trap of the standard C char array tools is that they all rely explicitly on the assumption that the character array includes a null terminator. If by oversight or error the null is omitted or overwritten, there's little to keep the C char array functions from manipulating the memory beyond the limits of the allocated space, sometimes with disastrous results.
C++ provides a vast improvement in the convenience and safety of string objects. For purposes of actual string handling operations, there are about the same number of distinct member function names in the string class as there are functions in the C library, but because of overloading the functionality is much greater. Coupled with sensible naming practices and the judicious use of default arguments, these features combine to make the string class much easier to use than the C library char array functions.
2-1-3-1. Appending, inserting, and concatenating strings▲
One of the most valuable and convenient aspects of C++ strings is that they grow as needed, without intervention on the part of the programmer. Not only does this make string-handling code inherently more trustworthy, it also almost entirely eliminates a tedious “housekeeping” chore—keeping track of the bounds of the storage where your strings live. For example, if you create a string object and initialize it with a string of 50 copies of ‘X', and later store in it 50 copies of “Zowie”, the object itself will reallocate sufficient storage to accommodate the growth of the data. Perhaps nowhere is this property more appreciated than when the strings manipulated in your code change size and you don't know how big the change is. The string member functions append( ) and insert( ) transparently reallocate storage when a string grows:
//: C03:StrSize.cpp
#include <string>
#include <iostream>
using namespace std;
int main() {
string bigNews("I saw Elvis in a UFO. ");
cout << bigNews << endl;
// How much data have we actually got?
cout << "Size = " <<
bigNews.size() << endl;
// How much can we store without reallocating?
cout << "Capacity = " <<
bigNews.capacity() << endl;
// Insert this string in bigNews immediately
// before bigNews[1]:
bigNews.insert(1, " thought I");
cout << bigNews << endl;
cout << "Size = " <<
bigNews.size() << endl;
cout << "Capacity = " <<
bigNews.capacity() << endl;
// Make sure that there will be this much space
bigNews.reserve(500);
// Add this to the end of the string:
bigNews.append("I've been working too
hard.");
cout << bigNews << endl;
cout << "Size = " <<
bigNews.size() << endl;
cout << "Capacity = " <<
bigNews.capacity() << endl;
} ///:~Here is the output from one particular compiler:
I saw Elvis in a UFO.
Size = 22
Capacity = 31
I thought I saw Elvis in a UFO.
Size = 32
Capacity = 47
I thought I saw Elvis in a UFO. I've been
working too hard.
Size = 59
Capacity = 511This example demonstrates that even though you can safely relinquish much of the responsibility for allocating and managing the memory your strings occupy, C++ strings provide you with several tools to monitor and manage their size. Notice the ease with which we changed the size of the storage allocated to the string. The size( ) function returns the number of characters currently stored in the string and is identical to the length( ) member function. The capacity( ) functionreturns the size of the current underlying allocation, meaning the number of characters the string can hold without requesting more storage. The reserve( ) function is an optimization mechanism that indicates your intention to specify a certain amount of storage for future use; capacity( ) always returns a value at least as large as the most recent call to reserve( ). A resize( ) function appends spaces if the new size is greater than the current string size or truncates the string otherwise. (An overload of resize( ) can specify a different character to append.)
The exact fashion that the string member functions allocate space for your data depends on the implementation of the library. When we tested one implementation with the previous example, it appeared that reallocations occurred on even word (that is, full-integer) boundaries, with one byte held back. The architects of the string class have endeavored to make it possible to mix the use of C char arrays and C++ string objects, so it is likely that figures reported by StrSize.cpp for capacity reflect that, in this particular implementation, a byte is set aside to easily accommodate the insertion of a null terminator.
2-1-3-2. Replacing string characters▲
The insert( ) functionis particularly nice because it absolves you from making sure the insertion of characters in a string won't overrun the storage space or overwrite the characters immediately following the insertion point. Space grows, and existing characters politely move over to accommodate the new elements. Sometimes this might not be what you want. If you want the size of the string to remain unchanged, use the replace( ) function to overwrite characters. There are a number of overloaded versions of replace( ), but the simplest one takes three arguments: an integer indicating where to start in the string, an integer indicating how many characters to eliminate from the original string, and the replacement string (which can be a different number of characters than the eliminated quantity). Here's a simple example:
//: C03:StringReplace.cpp
// Simple find-and-replace in strings.
#include <cassert>
#include <string>
using namespace std;
int main() {
string s("A piece of text");
string tag("$tag$");
s.insert(8, tag + ' ');
assert(s == "A piece $tag$
of text");
int start = s.find(tag);
assert(start == 8);
assert(tag.size() == 5);
s.replace(start, tag.size(), "hello
there");
assert(s == "A piece hello there of text");
} ///:~The tag is first inserted into s (notice that the insert happens before the value indicating the insert point and that an extra space was added after tag), and then it is found and replaced.
You should check to see if you've found anything before you perform a replace( ).The previous example replaces with a char*, but there's an overloaded version that replaces with a string.Here's a more complete demonstration replace( ):
//: C03:Replace.cpp
#include <cassert>
#include <cstddef> // For size_t
#include <string>
using namespace std;
void replaceChars(string& modifyMe,
const string& findMe, const string& newChars)
{
// Look in modifyMe for the "find string"
// starting at position 0:
size_t i = modifyMe.find(findMe, 0);
// Did we find the string to replace?
if(i != string::npos)
// Replace the find string with newChars:
modifyMe.replace(i, findMe.size(), newChars);
}
int main() {
string bigNews = "I thought I saw Elvis in a
UFO. "
"I have been working too
hard.";
string replacement("wig");
string findMe("UFO");
// Find "UFO" in bigNews and overwrite it:
replaceChars(bigNews, findMe, replacement);
assert(bigNews == "I thought I saw Elvis in a
"
"wig. I have been working too
hard.");
} ///:~If replace doesn't find the search string, it returns string::npos. The npos data member is a static constant member of the string class that represents a nonexistent character position.(33)
Unlike insert( ), replace( ) won't grow the string's storage space if you copy new characters into the middle of an existing series of array elements. However, it will grow the storage space if needed, for example, when you make a “replacement” that would expand the original string beyond the end of the current allocation. Here's an example:
//: C03:ReplaceAndGrow.cpp
#include <cassert>
#include <string>
using namespace std;
int main() {
string bigNews("I have been working the
grave.");
string replacement("yard shift.");
// The first argument says replace chars
// beyond the end of the existing string:
bigNews.replace(bigNews.size() - 1,
replacement.size(), replacement);
assert(bigNews == "I have been working the"
"graveyard shift.");
} ///:~The call to replace( ) begins “replacing” beyond the end of the existing array, which is equivalent to an append operation. Notice that in this example replace( ) expands the array accordingly.
You may have been hunting through this chapter trying to do something relatively simple such as replace all the instances of one character with a different character. Upon finding the previous material on replacing, you thought you found the answer, but then you started seeing groups of characters and counts and other things that looked a bit too complex. Doesn't string have a way to just replace one character with another everywhere?
You can easily write such a function using the find( ) and replace( ) member functions as follows:
//: C03:ReplaceAll.h
#ifndef REPLACEALL_H
#define REPLACEALL_H
#include <string>
std::string& replaceAll(std::string& context,
const std::string& from, const std::string&
to);
#endif // REPLACEALL_H ///:~//: C03:ReplaceAll.cpp {O}
#include <cstddef>
#include "ReplaceAll.h"
using namespace std;
string& replaceAll(string& context, const
string& from,
const string& to) {
size_t lookHere = 0;
size_t foundHere;
while((foundHere = context.find(from, lookHere))
!= string::npos) {
context.replace(foundHere, from.size(), to);
lookHere = foundHere + to.size();
}
return context;
} ///:~The version of find( ) used here takes as a second argument the position to start looking in and returns string::npos if it doesn't find it. It is important to advance the position held in the variable lookHere past the replacement string, in case from is a substring of to. The following program tests the replaceAll function:
//: C03:ReplaceAllTest.cpp
//{L} ReplaceAll
#include <cassert>
#include <iostream>
#include <string>
#include "ReplaceAll.h"
using namespace std;
int main() {
string text = "a man, a plan, a canal, Panama";
replaceAll(text, "an", "XXX");
assert(text == "a mXXX, a plXXX, a cXXXal, PXXXama");
} ///:~As you can see, the string class by itself doesn't solve all possible problems. Many solutions have been left to the algorithms in the Standard library(34) because the string class can look just like an STL sequence (by virtue of the iterators discussed earlier). All the generic algorithms work on a “range” of elements within a container. Usually that range is just “from the beginning of the container to the end.” A string object looks like a container of characters: to get the beginning of the range you use string::begin( ), and to get the end of the range you use string::end( ). The following example shows the use of the replace( ) algorithm to replace all the instances of the single character ‘X' with ‘Y':
//: C03:StringCharReplace.cpp
#include <algorithm>
#include <cassert>
#include <string>
using namespace std;
int main() {
string s("aaaXaaaXXaaXXXaXXXXaaa");
replace(s.begin(), s.end(), 'X', 'Y');
assert(s == "aaaYaaaYYaaYYYaYYYYaaa");
} ///:~Notice that this replace( ) is not called as a member function of string. Also, unlike the string::replace( ) functions that only perform one replacement, the replace( ) algorithm replaces all instances of one character with another.
The replace( ) algorithm only works with single objects (in this case, char objects) and will not replace quoted char arrays or string objects. Since a string behaves like an STL sequence, a number of other algorithms can be applied to it, which might solve other problems that are not directly addressed by the string member functions.
2-1-3-3. Concatenation using nonmember overloaded operators▲
One of the most delightful discoveries awaiting a C programmer learning about C++ string handling is how simply strings can be combined and appended using operator+ and operator+=.These operators make combining strings syntactically similar to adding numeric data:
//: C03:AddStrings.cpp
#include <string>
#include <cassert>
using namespace std;
int main() {
string s1("This ");
string s2("That ");
string s3("The other ");
// operator+ concatenates strings
s1 = s1 + s2;
assert(s1 == "This That ");
// Another way to concatenates strings
s1 += s3;
assert(s1 == "This That The other ");
// You can index the string on the right
s1 += s3 + s3[4] + "ooh lala";
assert(s1 == "This That The other The other oooh
lala");
} ///:~Using the operator+ and operator+= operatorsis a flexible andconvenient way to combine string data. On the right side of the statement, you can use almost any type that evaluates to a group of one or more characters.
2-1-4. Searching in strings▲
The find family of string member functions locates a character or group of characters within a given string. Here are the members of the find family and their general usage :
| string find member function | What/how it finds |
| find( ) | Searches a string for a specified character or group of characters and returns the starting position of the first occurrence found or npos if no match is found. |
| find_first_of( ) | Searches a target string and returns the position of the first match of any character in a specified group. If no match is found, it returns npos. |
| find_last_of( ) | Searches a target string and returns the position of the last match of any character in a specified group. If no match is found, it returns npos. |
| find_first_not_of( ) | Searches a target string and returns the position of the first element that doesn't match any character in a specified group. If no such element is found, it returns npos. |
| find_last_not_of( ) | Searches a target string and returns the position of the element with the largest subscript that doesn't match any character in a specified group. If no such element is found, it returns npos. |
| rfind( ) | Searches a string from end to beginning for a specified character or group of characters and returns the starting position of the match if one is found. If no match is found, it returns npos. |
The simplest use of find( ) searches for one or more characters in a string. This overloaded version of find( ) takes a parameter that specifies the character(s) for which to search and optionally a parameter that tells it where in the string to begin searching for the occurrence of a substring. (The default position at which to begin searching is 0.) By setting the call to find inside a loop, you can easily move through a string, repeating a search to find all the occurrences of a given character or group of characters within the string.
The following program uses the method of The Sieve of Eratosthenes to find prime numbers less than 50. This method starts with the number 2, marks all subsequent multiples of 2 as not prime, and repeats the process for the next prime candidate. The SieveTest constructor initializes sieveChars by setting the initial size of the character array and writing the value ‘P' to each of its members.
//: C03:Sieve.h
#ifndef SIEVE_H
#define SIEVE_H
#include <cmath>
#include <cstddef>
#include <string>
#include "../TestSuite/Test.h"
using std::size_t;
using std::sqrt;
using std::string;
class SieveTest : public TestSuite::Test {
string sieveChars;
public:
// Create a 50 char string and set each
// element to 'P' for Prime:
SieveTest() : sieveChars(50, 'P') {}
void run() {
findPrimes();
testPrimes();
}
bool isPrime(int p) {
if(p == 0 || p == 1) return false;
int root = int(sqrt(double(p)));
for(int i = 2; i <= root; ++i)
if(p % i == 0) return false;
return true;
}
void findPrimes() {
// By definition neither 0 nor 1 is prime.
// Change these elements to "N" for Not
Prime:
sieveChars.replace(0, 2, "NN");
// Walk through the array:
size_t sieveSize = sieveChars.size();
int root = int(sqrt(double(sieveSize)));
for(int i = 2; i <= root; ++i)
// Find all the multiples:
for(size_t factor = 2; factor * i < sieveSize;
++factor)
sieveChars[factor * i] = 'N';
}
void testPrimes() {
size_t i = sieveChars.find('P');
while(i != string::npos) {
test_(isPrime(i++));
i = sieveChars.find('P', i);
}
i = sieveChars.find_first_not_of('P');
while(i != string::npos) {
test_(!isPrime(i++));
i = sieveChars.find_first_not_of('P', i);
}
}
};
#endif // SIEVE_H ///:~//: C03:Sieve.cpp
//{L} ../TestSuite/Test
#include "Sieve.h"
int main() {
SieveTest t;
t.run();
return t.report();
} ///:~The find( ) function can walk forward through a string, detecting multiple occurrences of a character or a group of characters, and find_first_not_of( ) finds other characters or substrings.
There are no functions in the string class to change the case of a string, but you can easily create these functions using the Standard C library functions toupper( ) and tolower( ), which change the case of one character at a time. The following example illustrates a case-insensitive search:
//: C03:Find.h
#ifndef FIND_H
#define FIND_H
#include <cctype>
#include <cstddef>
#include <string>
#include "../TestSuite/Test.h"
using std::size_t;
using std::string;
using std::tolower;
using std::toupper;
// Make an uppercase copy of s
inline string upperCase(const string& s) {
string upper(s);
for(size_t i = 0; i < s.length(); ++i)
upper[i] = toupper(upper[i]);
return upper;
}
// Make a lowercase copy of s
inline string lowerCase(const string& s) {
string lower(s);
for(size_t i = 0; i < s.length(); ++i)
lower[i] = tolower(lower[i]);
return lower;
}
class FindTest : public TestSuite::Test {
string chooseOne;
public:
FindTest() : chooseOne("Eenie, Meenie, Miney,
Mo") {}
void testUpper() {
string upper = upperCase(chooseOne);
const string LOWER =
"abcdefghijklmnopqrstuvwxyz";
test_(upper.find_first_of(LOWER) == string::npos);
}
void testLower() {
string lower = lowerCase(chooseOne);
const string UPPER =
"ABCDEFGHIJKLMNOPQRSTUVWXYZ";
test_(lower.find_first_of(UPPER) == string::npos);
}
void testSearch() {
// Case sensitive search
size_t i = chooseOne.find("een");
test_(i == 8);
// Search lowercase:
string test = lowerCase(chooseOne);
i = test.find("een");
test_(i == 0);
i = test.find("een", ++i);
test_(i == 8);
i = test.find("een", ++i);
test_(i == string::npos);
// Search uppercase:
test = upperCase(chooseOne);
i = test.find("EEN");
test_(i == 0);
i = test.find("EEN", ++i);
test_(i == 8);
i = test.find("EEN", ++i);
test_(i == string::npos);
}
void run() {
testUpper();
testLower();
testSearch();
}
};
#endif // FIND_H ///:~//: C03:Find.cpp
//{L} ../TestSuite/Test
#include "Find.h"
#include "../TestSuite/Test.h"
int main() {
FindTest t;
t.run();
return t.report();
} ///:~Both the upperCase( ) and lowerCase( ) functions follow the same form: they make a copy of the argument string and change the case. The Find.cpp program isn't the best solution to the case-sensitivity problem, so we'll revisit it when we examine string comparisons.
2-1-4-1. Finding in reverse▲
If you need to search through a string from end to beginning (to find the data in “last in / first out” order), you can use the string member function rfind( ):
//: C03:Rparse.h
#ifndef RPARSE_H
#define RPARSE_H
#include <cstddef>
#include <string>
#include <vector>
#include "../TestSuite/Test.h"
using std::size_t;
using std::string;
using std::vector;
class RparseTest : public TestSuite::Test {
// To store the words:
vector<string> strings;
public:
void parseForData() {
// The ';' characters will be delimiters
string
s("now.;sense;make;to;going;is;This");
// The last element of the string:
int last = s.size();
// The beginning of the current word:
size_t current = s.rfind(';');
// Walk backward through the string:
while(current != string::npos) {
// Push each word into the vector.
// Current is incremented before copying
// to avoid copying the delimiter:
++current;
strings.push_back(s.substr(current, last - current));
// Back over the delimiter we just found,
// and set last to the end of the next word:
current -= 2;
last = current + 1;
// Find the next delimiter:
current = s.rfind(';', current);
}
// Pick up the first word -- it's not
// preceded by a delimiter:
strings.push_back(s.substr(0, last));
}
void testData() {
// Test them in the new order:
test_(strings[0] == "This");
test_(strings[1] == "is");
test_(strings[2] == "going");
test_(strings[3] == "to");
test_(strings[4] == "make");
test_(strings[5] == "sense");
test_(strings[6] == "now.");
string sentence;
for(size_t i = 0; i < strings.size() - 1; i++)
sentence += strings[i] += " ";
// Manually put last word in to avoid an extra
space:
sentence += strings[strings.size() - 1];
test_(sentence == "This is going to make sense
now.");
}
void run() {
parseForData();
testData();
}
};
#endif // RPARSE_H ///:~//: C03:Rparse.cpp
//{L} ../TestSuite/Test
#include "Rparse.h"
int main() {
RparseTest t;
t.run();
return t.report();
} ///:~The string member function rfind( ) backs through the string looking for tokens and reports the array index of matching characters or string::npos if it is unsuccessful.
2-1-4-2. Finding first/last of a set of characters▲
The find_first_of( ) and find_last_of( ) member functions can be conveniently put to work to create a little utility that will strip whitespace characters from both ends of a string. Notice that it doesn't touch the original string, but instead returns a new string:
//: C03:Trim.h
// General tool to strip spaces from both ends.
#ifndef TRIM_H
#define TRIM_H
#include <string>
#include <cstddef>
inline std::string trim(const std::string& s) {
if(s.length() == 0)
return s;
std::size_t beg = s.find_first_not_of("
\a\b\f\n\r\t\v");
std::size_t end = s.find_last_not_of("
\a\b\f\n\r\t\v");
if(beg == std::string::npos) // No non-spaces
return "";
return std::string(s, beg, end - beg + 1);
}
#endif // TRIM_H ///:~The first test checks for an empty string; in that case, no tests are made, and a copy is returned. Notice that once the end points are found, the string constructor builds a new string from the old one, giving the starting count and the length.
Testing such a general-purpose tool needs to be thorough:
//: C03:TrimTest.h
#ifndef TRIMTEST_H
#define TRIMTEST_H
#include "Trim.h"
#include "../TestSuite/Test.h"
class TrimTest : public TestSuite::Test {
enum {NTESTS = 11};
static std::string s[NTESTS];
public:
void testTrim() {
test_(trim(s[0]) == "abcdefghijklmnop");
test_(trim(s[1]) == "abcdefghijklmnop");
test_(trim(s[2]) == "abcdefghijklmnop");
test_(trim(s[3]) == "a");
test_(trim(s[4]) == "ab");
test_(trim(s[5]) == "abc");
test_(trim(s[6]) == "a b c");
test_(trim(s[7]) == "a b c");
test_(trim(s[8]) == "a \t b \t c");
test_(trim(s[9]) == "");
test_(trim(s[10]) == "");
}
void run() {
testTrim();
}
};
#endif // TRIMTEST_H ///:~//: C03:TrimTest.cpp {O}
#include "TrimTest.h"
// Initialize static data
std::string TrimTest::s[TrimTest::NTESTS] = {
" \t abcdefghijklmnop \t ",
"abcdefghijklmnop \t ",
" \t abcdefghijklmnop",
"a", "ab", "abc",
"a b c",
" \t a b c \t ", " \t a \t b \t c \t
",
"\t \n \r \v \f",
"" // Must also test the empty string
}; ///:~//: C03:TrimTestMain.cpp
//{L} ../TestSuite/Test TrimTest
#include "TrimTest.h"
int main() {
TrimTest t;
t.run();
return t.report();
} ///:~In the array of strings, you can see that the character arrays are automatically converted to string objects. This array provides cases to check the removal of spaces and tabs from both ends, as well as ensuring that spaces and tabs are not removed from the middle of a string.
2-1-4-3. Removing characters from strings▲
Removing characters is easy and efficient with the erase( ) member function, which takes two arguments: where to start removing characters (which defaults to 0), and how many to remove (which defaults to string::npos). If you specify more characters than remain in the string, the remaining characters are all erased anyway (so calling erase( ) without any arguments removes all characters from a string). Sometimes it's useful to take an HTML file and strip its tags and special characters so that you have something approximating the text that would be displayed in the Web browser, only as a plain text file. The following example uses erase( ) to do the job:
//: C03:HTMLStripper.cpp {RunByHand}
//{L} ReplaceAll
// Filter to remove html tags and markers.
#include <cassert>
#include <cmath>
#include <cstddef>
#include <fstream>
#include <iostream>
#include <string>
#include "ReplaceAll.h"
#include "../require.h"
using namespace std;
string& stripHTMLTags(string& s) {
static bool inTag = false;
bool done = false;
while(!done) {
if(inTag) {
// The previous line started an HTML tag
// but didn't finish. Must search for '>'.
size_t rightPos = s.find('>');
if(rightPos != string::npos) {
inTag = false;
s.erase(0, rightPos + 1);
}
else {
done = true;
s.erase();
}
}
else {
// Look for start of tag:
size_t leftPos = s.find('<');
if(leftPos != string::npos) {
// See if tag close is in this line:
size_t rightPos = s.find('>');
if(rightPos == string::npos) {
inTag = done = true;
s.erase(leftPos);
}
else
s.erase(leftPos, rightPos - leftPos + 1);
}
else
done = true;
}
}
// Remove all special HTML characters
replaceAll(s, "<",
"<");
replaceAll(s, ">",
">");
replaceAll(s, "&",
"&");
replaceAll(s, " ", " ");
// Etc...
return s;
}
int main(int argc, char* argv[]) {
requireArgs(argc, 1,
"usage: HTMLStripper InputFile");
ifstream in(argv[1]);
assure(in, argv[1]);
string s;
while(getline(in, s))
if(!stripHTMLTags(s).empty())
cout << s << endl;
} ///:~This example will even strip HTML tags that span multiple lines.(35) This is accomplished with the static flag, inTag, which is true whenever the start of a tag is found, but the accompanying tag end is not found in the same line. All forms of erase( ) appear in the stripHTMLFlags( ) function.(36) The version of getline( ) we use here is a (global) function declared in the <string> header and is handy because it stores an arbitrarily long line in its string argument. You don't need to worry about the dimension of a character array as you do with istream::getline( ). Notice that this program uses the replaceAll( ) function from earlier in this chapter. In the next chapter, we'll use string streams to create a more elegant solution.
2-1-4-4. Comparing strings▲
Comparing strings is inherently different from comparing numbers. Numbers have constant, universally meaningful values. To evaluate the relationship between the magnitudes of two strings, you must make a lexical comparison. Lexical comparison means that when you test a character to see if it is “greater than” or “less than” another character, you are actually comparing the numeric representation of those characters as specified in the collating sequence of the character set being used. Most often this will be the ASCII collating sequence, which assigns the printable characters for the English language numbers in the range 32 through 127 decimal. In the ASCII collating sequence, the first “character” in the list is the space, followed by several common punctuation marks, and then uppercase and lowercase letters. With respect to the alphabet, this means that the letters nearer the front have lower ASCII values than those nearer the end. With these details in mind, it becomes easier to remember that when a lexical comparison that reports s1 is “greater than” s2, it simply means that when the two were compared, the first differing character in s1 came later in the alphabet than the character in that same position in s2.
C++ provides several ways to compare strings, and each has advantages. The simplest to use are the nonmember, overloaded operator functions: operator ==, operator != operator >, operator <, operator >=,and operator <=.
//: C03:CompStr.h
#ifndef COMPSTR_H
#define COMPSTR_H
#include <string>
#include "../TestSuite/Test.h"
using std::string;
class CompStrTest : public TestSuite::Test {
public:
void run() {
// Strings to compare
string s1("This");
string s2("That");
test_(s1 == s1);
test_(s1 != s2);
test_(s1 > s2);
test_(s1 >= s2);
test_(s1 >= s1);
test_(s2 < s1);
test_(s2 <= s1);
test_(s1 <= s1);
}
};
#endif // COMPSTR_H ///:~//: C03:CompStr.cpp
//{L} ../TestSuite/Test
#include "CompStr.h"
int main() {
CompStrTest t;
t.run();
return t.report();
} ///:~The overloaded comparison operators are useful for comparing both full strings and individual string character elements.
Notice in the following example the flexibility of argument types on both the left and right side of the comparison operators. For efficiency, the string class provides overloaded operators for the direct comparison of string objects, quoted literals, and pointers to C-style strings without having to create temporary string objects.
//: C03:Equivalence.cpp
#include <iostream>
#include <string>
using namespace std;
int main() {
string s2("That"), s1("This");
// The lvalue is a quoted literal
// and the rvalue is a string:
if("That" == s2)
cout << "A match" << endl;
// The left operand is a string and the right is
// a pointer to a C-style null terminated string:
if(s1 != s2.c_str())
cout << "No match" << endl;
} ///:~The c_str( ) function returns a const char* that points to a C-style, null-terminated string equivalent to the contents of the string object. This comes in handy when you want to pass a string to a standard C function, such as atoi( ) or any of the functions defined in the <cstring> header. It is an error to use the value returned by c_str( ) as non-const argument to any function.
You won't find the logical not (!) or the logical comparison operators (&& and ||) among operators for a string. (Neither will you find overloaded versions of the bitwise C operators &, |, ^, or ~.) The overloaded nonmember comparison operators for the string class are limited to the subset that has clear, unambiguous application to single characters or groups of characters.
The compare( ) member function offers you a great deal more sophisticated and precise comparison than the nonmember operator set. It provides overloaded versions to compare:
- Two complete strings.
- Part of either string to a complete string.
- Subsets of two strings.
The following example compares complete strings:
//: C03:Compare.cpp
// Demonstrates compare() and swap().
#include <cassert>
#include <string>
using namespace std;
int main() {
string first("This");
string second("That");
assert(first.compare(first) == 0);
assert(second.compare(second) == 0);
// Which is lexically greater?
assert(first.compare(second) > 0);
assert(second.compare(first) < 0);
first.swap(second);
assert(first.compare(second) < 0);
assert(second.compare(first) > 0);
} ///:~The swap( ) function in this example does what its name implies: it exchanges the contents of its object and argument. To compare a subset of the characters in one or both strings, you add arguments that define where to start the comparison and how many characters to consider. For example, we can use the following overloaded version of compare( ):
s1.compare(s1StartPos, s1NumberChars, s2, s2StartPos, s2NumberChars);
Here's an example:
//: C03:Compare2.cpp
// Illustrate overloaded compare().
#include <cassert>
#include <string>
using namespace std;
int main() {
string first("This is a day that will live in
infamy");
string second("I don't believe that this is what
"
"I signed up for");
// Compare "his is" in both strings:
assert(first.compare(1, 7, second, 22, 7) == 0);
// Compare "his is a" to "his is w":
assert(first.compare(1, 9, second, 22, 9) < 0);
} ///:~In the examples so far, we have used C-style array indexing syntax to refer to an individual character in a string. C++ strings provide an alternative to the s[n] notation: the at( ) member. These two indexing mechanisms produce the same result in C++ if all goes well:
//: C03:StringIndexing.cpp
#include <cassert>
#include <string>
using namespace std;
int main() {
string s("1234");
assert(s[1] == '2');
assert(s.at(1) == '2');
} ///:~There is one important difference, however, between [ ] and at( ). When you try to reference an array element that is out of bounds, at( ) will do you the kindness of throwing an exception, while ordinary [ ] subscripting syntax will leave you to your own devices:
//: C03:BadStringIndexing.cpp
#include <exception>
#include <iostream>
#include <string>
using namespace std;
int main() {
string s("1234");
// at() saves you by throwing an exception:
try {
s.at(5);
} catch(exception& e) {
cerr << e.what() << endl;
}
} ///:~Responsible programmers will not use errant indexes, but should you want to benefits of automatic index checking, using at( ) in place of [ ] will give you a chance to gracefully recover from references to array elements that don't exist. Execution of this program on one of our test compilers gave the following output:
invalid string positionThe at( ) member throws an object of class out_of_range, which derives (ultimately) from std::exception. By catching this object in an exception handler, you can take appropriate remedial actions such as recalculating the offending subscript or growing the array. Using string::operator[ ]( ) gives no such protection and is as dangerous as char array processing in C.(37)
2-1-4-5. Strings and character traits▲
The program Find.cpp earlier in this chapter leads us to ask the obvious question: Why isn't case-insensitive comparison part of the standard string class? The answer provides interesting background on the true nature of C++ string objects.
Consider what it means for a character to have “case.” Written Hebrew, Farsi, and Kanji don't use the concept of upper- and lowercase, so for those languages this idea has no meaning. It would seem that if there were a way to designate some languages as “all uppercase” or “all lowercase,” we could design a generalized solution. However, some languages that employ the concept of “case” also change the meaning of particular characters with diacritical marks, for example: the cedilla in Spanish, the circumflex in French, and the umlaut in German. For this reason, any case-sensitive collating scheme that attempts to be comprehensive will be nightmarishly complex to use.
Although we usually treat the C++ string as a class, this is really not the case. The string type is a specialization of a more general constituent, the basic_string< > template. Observe how string is declared in the Standard C++ header file:(38)
typedef basic_string<char> string;To understand the nature of the string class, look at the basic_string< > template:
template<class charT, class traits =
char_traits<charT>,
class allocator =
allocator<charT> > class basic_string;In Chapter 5, we examine templates in great detail (much more than in Chapter 16 of Volume 1). For now, just notice that the string type is created when the basic_string template is instantiated with char. Inside the basic_string< > template declaration, the line:
class traits = char_traits<charT>,tells us that the behavior of the class made from the basic_string< > template is specified by a class based on the template char_traits< >. Thus, the basic_string< > template produces string-oriented classes that manipulate types other than char (wide characters, for example). To do this, the char_traits< > template controls the content and collating behaviors of a variety of character sets using the character comparison functions eq( ) (equal), ne( ) (not equal), and lt( ) (less than). The basic_string< > string comparison functions rely on these.
This is why the string class doesn't include case-insensitive member functions: that's not in its job description. To change the way the string class treats character comparison, you must supply a different char_traits< > template because that defines the behavior of the individual character comparison member functions.
You can use this information to make a new type of string class that ignores case. First, we'll define a new case-insensitive char_traits< > template that inherits from the existing template. Next, we'll override only the members we need to change to make character-by-character comparison case insensitive. (In addition to the three lexical character comparison members mentioned earlier, we'll also supply a new implementation for the char_traits functions find( ) and compare( )) . Finally, we'll typedef a new class based on basic_string, but using the case-insensitive ichar_traits template for its second argument:
//: C03:ichar_traits.h
// Creating your own character traits.
#ifndef ICHAR_TRAITS_H
#define ICHAR_TRAITS_H
#include <cassert>
#include <cctype>
#include <cmath>
#include <cstddef>
#include <ostream>
#include <string>
using std::allocator;
using std::basic_string;
using std::char_traits;
using std::ostream;
using std::size_t;
using std::string;
using std::toupper;
using std::tolower;
struct ichar_traits : char_traits<char> {
// We'll only change character-by-
// character comparison functions
static bool eq(char c1st, char c2nd) {
return toupper(c1st) == toupper(c2nd);
}
static bool ne(char c1st, char c2nd) {
return !eq(c1st, c2nd);
}
static bool lt(char c1st, char c2nd) {
return toupper(c1st) < toupper(c2nd);
}
static int
compare(const char* str1, const char* str2, size_t n)
{
for(size_t i = 0; i < n; ++i) {
if(str1 == 0)
return -1;
else if(str2 == 0)
return 1;
else if(tolower(*str1) < tolower(*str2))
return -1;
else if(tolower(*str1) > tolower(*str2))
return 1;
assert(tolower(*str1) == tolower(*str2));
++str1; ++str2; // Compare the other chars
}
return 0;
}
static const char*
find(const char* s1, size_t n, char c) {
while(n-- > 0)
if(toupper(*s1) == toupper(c))
return s1;
else
++s1;
return 0;
}
};
typedef basic_string<char, ichar_traits> istring;
inline ostream& operator<<(ostream& os,
const istring& s) {
return os << string(s.c_str(), s.length());
}
#endif // ICHAR_TRAITS_H ///:~We provide a typedef named istring so that our class will act like an ordinary string in every way, except that it will make all comparisons without respect to case. For convenience, we've also provided an overloaded operator<<( ) so that you can print istrings. Here's an example:
//: C03:ICompare.cpp
#include <cassert>
#include <iostream>
#include "ichar_traits.h"
using namespace std;
int main() {
// The same letters except for case:
istring first = "tHis";
istring second = "ThIS";
cout << first << endl;
cout << second << endl;
assert(first.compare(second) == 0);
assert(first.find('h') == 1);
assert(first.find('I') == 2);
assert(first.find('x') == string::npos);
} ///:~This is just a toy example. To make istring fully equivalent to string, we'd have to create the other functions necessary to support the new istring type.
The <string> header provides a wide string class via the following typedef:
typedef basic_string<wchar_t> wstring;Wide string support also reveals itself in wide streams (wostream in place of ostream, also defined in <iostream>) and in the header <cwctype>, a wide-character version of <cctype>. This along with the wchar_t specialization of char_traits in the standard library allows us to do a wide-character version of ichar_traits:
//: C03:iwchar_traits.h {-g++}
// Creating your own wide-character traits.
#ifndef IWCHAR_TRAITS_H
#define IWCHAR_TRAITS_H
#include <cassert>
#include <cmath>
#include <cstddef>
#include <cwctype>
#include <ostream>
#include <string>
using std::allocator;
using std::basic_string;
using std::char_traits;
using std::size_t;
using std::towlower;
using std::towupper;
using std::wostream;
using std::wstring;
struct iwchar_traits : char_traits<wchar_t> {
// We'll only change character-by-
// character comparison functions
static bool eq(wchar_t c1st, wchar_t c2nd) {
return towupper(c1st) == towupper(c2nd);
}
static bool ne(wchar_t c1st, wchar_t c2nd) {
return towupper(c1st) != towupper(c2nd);
}
static bool lt(wchar_t c1st, wchar_t c2nd) {
return towupper(c1st) < towupper(c2nd);
}
static int compare(
const wchar_t* str1, const wchar_t* str2, size_t n)
{
for(size_t i = 0; i < n; i++) {
if(str1 == 0)
return -1;
else if(str2 == 0)
return 1;
else if(towlower(*str1) < towlower(*str2))
return -1;
else if(towlower(*str1) > towlower(*str2))
return 1;
assert(towlower(*str1) == towlower(*str2));
++str1; ++str2; // Compare the other wchar_ts
}
return 0;
}
static const wchar_t*
find(const wchar_t* s1, size_t n, wchar_t c) {
while(n-- > 0)
if(towupper(*s1) == towupper(c))
return s1;
else
++s1;
return 0;
}
};
typedef basic_string<wchar_t, iwchar_traits>
iwstring;
inline wostream& operator<<(wostream& os,
const iwstring& s) {
return os << wstring(s.c_str(), s.length());
}
#endif // IWCHAR_TRAITS_H ///:~As you can see, this is mostly an exercise in placing a ‘w' in the appropriate place in the source code. The test program looks like this:
//: C03:IWCompare.cpp {-g++}
#include <cassert>
#include <iostream>
#include "iwchar_traits.h"
using namespace std;
int main() {
// The same letters except for case:
iwstring wfirst = L"tHis";
iwstring wsecond = L"ThIS";
wcout << wfirst << endl;
wcout << wsecond << endl;
assert(wfirst.compare(wsecond) == 0);
assert(wfirst.find('h') == 1);
assert(wfirst.find('I') == 2);
assert(wfirst.find('x') == wstring::npos);
} ///:~Unfortunately, some compilers still do not provide robust support for wide characters.
2-1-5. A string application▲
If you've looked at the sample code in this book closely, you've noticed that certain tokens in the comments surround the code. These are used by a Python program that Bruce wrote to extract the code into files and set up makefiles for building the code. For example, a double-slash followed by a colon at the beginning of a line denotes the first line of a source file. The rest of the line contains information describing the file's name and location and whether it should be only compiled rather than fully built into an executable file. For example, the first line in the previous program above contains the string C03:IWCompare.cpp, indicating that the file IWCompare.cpp should be extracted into the directory C03.
The last line of a source file contains a triple-slash followed by a colon and a tilde. If the first line has an exclamation point immediately after the colon, the first and last lines of the source code are not to be output to the file (this is for data-only files). (If you're wondering why we're avoiding showing you these tokens, it's because we don't want to break the code extractor when applied to the text of the book!)
Bruce's Python program does a lot more than just extract code. If the token “{O}” follows the file name, its makefile entry will only be set up to compile the file and not to link it into an executable. (The Test Framework in Chapter 2 is built this way.) To link such a file with another source example, the target executable's source file will contain an “{L}” directive, as in:
//{L} ../TestSuite/TestThis section will present a program to just extract all the code so that you can compile and inspect it manually. You can use this program to extract all the code in this book by saving the document file as a text file(39) (let's call it TICV2.txt) and by executing something like the following on a shell command line:
C:> extractCode TICV2.txt /TheCodeThis command reads the text file TICV2.txt and writes all the source code files in subdirectories under the top-level directory /TheCode. The directory tree will look like the following:
TheCode/
C0B/
C01/
C02/
C03/
C04/
C05/
C06/
C07/
C08/
C09/
C10/
C11/
TestSuite/The source files containing the examples from each chapter will be in the corresponding directory.
Here's the program:
//: C03:ExtractCode.cpp {-edg} {RunByHand}
// Extracts code from text.
#include <cassert>
#include <cstddef>
#include <cstdio>
#include <cstdlib>
#include <fstream>
#include <iostream>
#include <string>
using namespace std;
// Legacy non-standard C header for mkdir()
#if defined(__GNUC__) || defined(__MWERKS__)
#include <sys/stat.h>
#elif defined(__BORLANDC__) || defined(_MSC_VER) \
|| defined(__DMC__)
#include <direct.h>
#else
#error Compiler not supported
#endif
// Check to see if directory exists
// by attempting to open a new file
// for output within it.
bool exists(string fname) {
size_t len = fname.length();
if(fname[len-1] != '/' && fname[len-1] !=
'\\')
fname.append("/");
fname.append("000.tmp");
ofstream outf(fname.c_str());
bool existFlag = outf;
if(outf) {
outf.close();
remove(fname.c_str());
}
return existFlag;
}
int main(int argc, char* argv[]) {
// See if input file name provided
if(argc == 1) {
cerr << "usage: extractCode file
[dir]" << endl;
exit(EXIT_FAILURE);
}
// See if input file exists
ifstream inf(argv[1]);
if(!inf) {
cerr << "error opening file: "
<< argv[1] << endl;
exit(EXIT_FAILURE);
}
// Check for optional output directory
string root("./"); // current is default
if(argc == 3) {
// See if output directory exists
root = argv[2];
if(!exists(root)) {
cerr << "no such directory: "
<< root << endl;
exit(EXIT_FAILURE);
}
size_t rootLen = root.length();
if(root[rootLen-1] != '/' &&
root[rootLen-1] != '\\')
root.append("/");
}
// Read input file line by line
// checking for code delimiters
string line;
bool inCode = false;
bool printDelims = true;
ofstream outf;
while(getline(inf, line)) {
size_t findDelim = line.find("//"
"/:~");
if(findDelim != string::npos) {
// Output last line and close file
if(!inCode) {
cerr << "Lines out of order"
<< endl;
exit(EXIT_FAILURE);
}
assert(outf);
if(printDelims)
outf << line << endl;
outf.close();
inCode = false;
printDelims = true;
} else {
findDelim = line.find("//"
":");
if(findDelim == 0) {
// Check for '!' directive
if(line[3] == '!') {
printDelims = false;
++findDelim; // To skip '!' for next search
}
// Extract subdirectory name, if any
size_t startOfSubdir =
line.find_first_not_of(" \t",
findDelim+3);
findDelim = line.find(':', startOfSubdir);
if(findDelim == string::npos) {
cerr << "missing filename
information\n" << endl;
exit(EXIT_FAILURE);
}
string subdir;
if(findDelim > startOfSubdir)
subdir = line.substr(startOfSubdir,
findDelim -
startOfSubdir);
// Extract file name (better be one!)
size_t startOfFile = findDelim + 1;
size_t endOfFile =
line.find_first_of(" \t",
startOfFile);
if(endOfFile == startOfFile) {
cerr << "missing filename"
<< endl;
exit(EXIT_FAILURE);
}
// We have all the pieces; build fullPath name
string fullPath(root);
if(subdir.length() > 0)
fullPath.append(subdir).append("/");
assert(fullPath[fullPath.length()-1] == '/');
if(!exists(fullPath))
#if defined(__GNUC__) || defined(__MWERKS__)
mkdir(fullPath.c_str(), 0); // Create subdir
#else
mkdir(fullPath.c_str()); // Create subdir
#endif
fullPath.append(line.substr(startOfFile,
endOfFile - startOfFile));
outf.open(fullPath.c_str());
if(!outf) {
cerr << "error opening "
<< fullPath
<< " for output"
<< endl;
exit(EXIT_FAILURE);
}
inCode = true;
cout << "Processing " <<
fullPath << endl;
if(printDelims)
outf << line << endl;
}
else if(inCode) {
assert(outf);
outf << line << endl; // Output middle
code line
}
}
}
exit(EXIT_SUCCESS);
} ///:~First, you'll notice some conditional compilation directives. The mkdir( ) function, which creates a directory in the file system, is defined by the POSIX(40) standard in the header <sys/stat.h>. Unfortunately, many compilers still use a different header (<direct.h>). The respective signatures for mkdir( ) also differ: POSIX specifies two arguments, the older versions just one. For this reason, there is more conditional compilation later in the program to choose the right call to mkdir( ). We normally don't use conditional compilation in the examples in this book, but this particular program is too useful not to put a little extra work into, since you can use it to extract all the code with it.
The exists( ) function in ExtractCode.cpp tests whether a directory exists by opening a temporary file in it. If the open fails, the directory doesn't exist. You remove a file by sending its name as a char* to std::remove( ).
The main program validates the command-line arguments and then reads the input file a line at a time, looking for the special source code delimiters. The Boolean flag inCode indicates that the program is in the middle of a source file, so lines should be output. The printDelims flag will be true if the opening token is not followed by an exclamation point; otherwise the first and last lines are not written. It is important to check for the closing delimiter first, because the start token is a subset, and searching for the start token first would return a successful find for both cases. If we encounter the closing token, we verify that we are in the middle of processing a source file; otherwise, something is wrong with the way the delimiters are laid out in the text file. If inCode is true, all is well, and we (optionally) write the last line and close the file. When the opening token is found, we parse the directory and file name components and open the file. The following string-related functions were used in this example: length( ), append( ), getline( ), find( ) (two versions), find_first_not_of( ), substr( ), find_first_of( ), c_str( ), and, of course, operator<<( ).
2-1-6. Summary▲
C++ string objects provide developers with a number of great advantages over their C counterparts. For the most part, the string class makes referring to strings with character pointers unnecessary. This eliminates an entire class of software defects that arise from the use of uninitialized and incorrectly valued pointers.
C++ strings dynamically and transparently grow their internal data storage space to accommodate increases in the size of the string data. When the data in a string grows beyond the limits of the memory initially allocated to it, the string object will make the memory management calls that take space from and return space to the heap. Consistent allocation schemes prevent memory leaks and have the potential to be much more efficient than “roll your own” memory management.
The string class member functions provide a fairly comprehensive set of tools for creating, modifying, and searching in strings. String comparisons are always case sensitive, but you can work around this by copying string data to C-style null-terminated strings and using case-insensitive string comparison functions, temporarily converting the data held in string objects to a single case, or by creating a case-insensitive string class that overrides the character traits used to create the basic_string object.
2-1-7. Exercises▲
Solutions to selected exercises can be found in the electronic document The Thinking in C++ Volume 2 Annotated Solution Guide, available for a small fee from www.MindView.net.
- Write and test a function that reverses the order of the characters in a string.
- A palindrome is a word or group of words that read the same forward and backward. For example “madam” or “wow.” Write a program that takes a string argument from the command line and, using the function from the previous exercise, prints whether the string was a palindrome or not.
- Make your program from Exercise 2 return true even if symmetric letters differ in case. For example, “Civic” would still return true although the first letter is capitalized.
- Change your program from Exercise 3 to ignore punctuation and spaces as well. For example “Able was I, ere I saw Elba.” would report true.
- Using the following string declarations and only chars (no
string literals or magic numbers):
string one("I walked down the canyon with the moving mountain bikers.");
string two("The bikers passed by me too close for comfort.");
string three("I went hiking instead.");
produce the following sentence:
I moved down the canyon with the mountain bikers. The mountain bikers passed by me too close for comfort. So I went hiking instead. - Write a program named replace that takes three command-line arguments representing an input text file, a string to replace (call it from), and a replacement string (call it to). The program should write a new file to standard output with all occurrences of from replaced by to.
- Repeat the previous exercise but replace all instances of from regardless of case.
- Make your program from Exercise 3 take a filename from the command-line, and then display all words that are palindromes (ignoring case) in the file. Do not display duplicates (even if their case differs). Do not try to look for palindromes that are larger than a word (unlike in Exercise 4).
- Modify HTMLStripper.cpp so that when it encounters a tag, it displays the tag's name, then displays the file's contents between the tag and the file's ending tag. Assume no nesting of tags, and that all tags have ending tags (denoted with </TAGNAME>).
- Write a program that takes three command-line arguments (a filename and two strings) and displays to the console all lines in the file that have both strings in the line, either string, only one string, or neither string, based on user input at the beginning of the program (the user will choose which matching mode to use). For all but the “neither string” option, highlight the input string(s) by placing an asterisk (*) at the beginning and end of each string's occurrence when it is displayed.
- Write a program that takes two command-line arguments (a filename and a string) and counts the number of times the string occurs in the file, even as a substring (but ignoring overlaps). For example, an input string of “ba” would match twice in the word “basketball,” but an input string of “ana” would match only once in the word “banana.” Display to the console the number of times the string is matched in the file, as well as the average length of the words where the string occurred. (If the string occurs more than once in a word, only count the word once in figuring the average.)
- Write a program that takes a filename from the command line and
profiles the character usage, including punctuation and spaces (all character
values of 0x21 [33] through 0x7E [126], as well as the space character). That is,
count the number of occurrences of each character in the file, then display the
results sorted either sequentially (space, then !, ", #, etc.) or by
ascending or descending frequency based on user input at the beginning of the
program. For space, display the word “Space” instead of the character ' '. A
sample run might look something like this:
Format sequentially, ascending, or descending (S/A/D): D
t: 526
r: 490
etc. - Using find( ) and rfind( ), write a program that takes two command-line arguments (a filename and a string) and displays the first and last words (and their indexes) not matching the string, as well as the indexes of the first and last instances of the string. Display “Not Found” if any of the searches fail.
- Using the find_first_of “family” of functions (but not exclusively), write a program that will remove all non-alphanumeric characters except spaces and periods from a file, then capitalize the first letter following a period.
- Again using the find_first_of “family” of functions, write a program that accepts a filename as a command-line argument and then formats all numbers in the file to currency. Ignore decimal points after the first until a non-numeric character is found, and round to the nearest hundredth. For example, the string 12.399abc29.00.6a would be formatted (in the USA) to $12.40abc$29.01a.
- Write a program that accepts two command-line arguments (a filename and a number) and scrambles each word in the file by randomly switching two of its letters the number of times specified in the second argument. (That is, if 0 is passed into your program from the command-line, the words should not be scrambled; if 1 is passed in, one pair of randomly-chosen letters should be swapped, for an input of 2, two random pairs should be swapped, etc.).
- Write a program that accepts a filename from the command line and displays the number of sentences (defined as the number of periods in the file), average number of characters per sentence, and the total number of characters in the file.
- Prove to yourself that the at( ) member function really will throw an exception if an attempt is made to go out of bounds, and that the indexing operator ([ ]) won't.
2-2. Iostreams▲
You can do much more with the general I/O problem than just take standard I/O and turn it into a class.
Wouldn't it be nice if you could make all the usual “receptacles”—standard I/O, files, and even blocks of memory—look the same so that you need to remember only one interface? That's the idea behind iostreams. They're much easier, safer, and sometimes even more efficient than the assorted functions from the Standard C stdio library.
The iostreams classes are usually the first part of the C++ library that new C++ programmers learn to use. This chapter discusses how iostreams are an improvement over C's stdio facilities and explores the behavior of file and string streams in addition to the standard console streams.
2-2-1. Why iostreams?▲
You might wonder what's wrong with the good old C library. Why not “wrap” the C library in a class and be done with it? Sometimes this is a fine solution. For example, suppose you want to make sure that the file represented by a stdio FILE pointer is always safely opened and properly closed without having to rely on the user to remember to call the close( ) function. The following program is such an attempt:
//: C04:FileClass.h
// stdio files wrapped.
#ifndef FILECLASS_H
#define FILECLASS_H
#include <cstdio>
#include <stdexcept>
class FileClass {
std::FILE* f;
public:
struct FileClassError : std::runtime_error {
FileClassError(const char* msg)
: std::runtime_error(msg) {}
};
FileClass(const char* fname, const char* mode =
"r");
~FileClass();
std::FILE* fp();
};
#endif // FILECLASS_H ///:~When you perform file I/O in C, you work with a naked pointer to a FILE struct, but this class wraps around the pointer and guarantees it is properly initialized and cleaned up using the constructor and destructor. The second constructor argument is the file mode, which defaults to “r” for “read.”
To fetch the value of the pointer to use in the file I/O functions, you use the fp( ) access function. Here are the member function definitions:
//: C04:FileClass.cpp {O}
// FileClass Implementation.
#include "FileClass.h"
#include <cstdlib>
#include <cstdio>
using namespace std;
FileClass::FileClass(const char* fname, const char*
mode) {
if((f = fopen(fname, mode)) == 0)
throw FileClassError("Error opening
file");
}
FileClass::~FileClass() { fclose(f); }
FILE* FileClass::fp() { return
f; } ///:~The constructor calls fopen( ), as you would normally do, but it also ensures that the result isn't zero, which indicates a failure upon opening the file. If the file does not open as expected, an exception is thrown.
The destructor closes the file, and the access function fp( ) returns f. Here's a simple example using FileClass:
//: C04:FileClassTest.cpp
//{L} FileClass
#include <cstdlib>
#include <iostream>
#include "FileClass.h"
using namespace std;
int main() {
try {
FileClass f("FileClassTest.cpp");
const int BSIZE = 100;
char buf[BSIZE];
while(fgets(buf, BSIZE, f.fp()))
fputs(buf, stdout);
} catch(FileClass::FileClassError& e) {
cout << e.what() << endl;
return EXIT_FAILURE;
}
return EXIT_SUCCESS;
} // File automatically closed by destructor
///:~You create the FileClass object and use it in normal C file I/O function calls by calling fp( ). When you're done with it, just forget about it; the file is closed by the destructor at the end of its scope.
Even though the FILE pointer is private, it isn't particularly safe because fp( ) retrieves it. Since the only effect seems to be guaranteed initialization and cleanup, why not make it public or use a struct instead? Notice that while you can get a copy of f using fp( ), you cannot assign to f—that's completely under the control of the class. After capturing the pointer returned by fp( ), the client programmer can still assign to the structure elements or even close it, so the safety is in guaranteeing a valid FILE pointer rather than proper contents of the structure.
If you want complete safety, you must prevent the user from directly accessing the FILE pointer. Some version of all the normal file I/O functions must show up as class members so that everything you can do with the C approach is available in the C++ class:
//: C04:Fullwrap.h
// Completely hidden file IO.
#ifndef FULLWRAP_H
#define FULLWRAP_H
#include <cstddef>
#include <cstdio>
#undef getc
#undef putc
#undef ungetc
using std::size_t;
using std::fpos_t;
class File {
std::FILE* f;
std::FILE* F(); // Produces checked pointer to f
public:
File(); // Create object but don't open file
File(const char* path, const char* mode =
"r");
~File();
int open(const char* path, const char* mode =
"r");
int reopen(const char* path, const char* mode);
int getc();
int ungetc(int c);
int putc(int c);
int puts(const char* s);
char* gets(char* s, int n);
int printf(const char* format, ...);
size_t read(void* ptr, size_t size, size_t n);
size_t write(const void* ptr, size_t size, size_t n);
int eof();
int close();
int flush();
int seek(long offset, int whence);
int getpos(fpos_t* pos);
int setpos(const fpos_t* pos);
long tell();
void rewind();
void setbuf(char* buf);
int setvbuf(char* buf, int type, size_t sz);
int error();
void clearErr();
};
#endif // FULLWRAP_H ///:~This class contains almost all the file I/O functions from <cstdio>. (vfprintf( ) is missing; it implements the printf( ) member function.)
File has the same constructor as in the previous example, and it also has a default constructor. The default constructor is important if you want to create an array of File objects or use a File object as a member of another class where the initialization doesn't happen in the constructor, but some time after the enclosing object is created.
The default constructor sets the private FILE pointer f to zero. But now, before any reference to f, its value must be checked to ensure it isn't zero. This is accomplished with F( ), which is private because it is intended to be used only by other member functions. (We don't want to give the user direct access to the underlying FILE structure in this class.)
This approach is not a terrible solution by any means. It's quite functional, and you could imagine making similar classes for standard (console) I/O and for in-core formatting (reading/writing a piece of memory rather than a file or the console).
The stumbling block is the runtime interpreter used for the variable argument list functions. This is the code that parses your format string at runtime and grabs and interprets arguments from the variable argument list. It's a problem for four reasons.
- Even if you use only a fraction of the functionality of the interpreter, the whole thing gets loaded into your executable. So if you say printf("%c", 'x');, you'll get the whole package, including the parts that print floating-point numbers and strings. There's no standard option for reducing the amount of space used by the program.
- Because the interpretation happens at runtime, you can't get rid of a performance overhead. It's frustrating because all the information is there in the format string at compile time, but it's not evaluated until runtime. However, if you could parse the arguments in the format string at compile time, you could make direct function calls that have the potential to be much faster than a runtime interpreter (although the printf( ) family of functions is usually quite well optimized).
- Because the format string is not evaluated until runtime, there can be no compile-time error checking. You're probably familiar with this problem if you've tried to find bugs that came from using the wrong number or type of arguments in a printf( ) statement. C++ makes a big deal out of compile-time error checking to find errors early and make your life easier. It seems a shame to throw type safety away for an I/O library, especially since I/O is used a lot.
- For C++, the most crucial problem is that the printf( ) family of functions is not particularly extensible. They're really designed to handle only the basic data types in C (char, int, float, double, wchar_t, char*, wchar_t*, and void*) and their variations. You might think that every time you add a new class, you could add overloaded printf( ) and scanf( ) functions (and their variants for files and strings), but remember, overloaded functions must have different types in their argument lists, and the printf( ) family hides its type information in the format string and in the variable argument list. For a language such as C++, whose goal is to be able to easily add new data types, this is an unacceptable restriction.
2-2-2. Iostreams to the rescue▲
These issues make it clear that I/O is one of the first priorities for the Standard C++ class libraries. Because “hello, world” is the first program just about everyone writes in a new language, and because I/O is part of virtually every program, the I/O library in C++ must be particularly easy to use. It also has the much greater challenge that it must accommodate any new class. Thus, its constraints require that this foundation class library be a truly inspired design. In addition to gaining a great deal of leverage and clarity in your dealings with I/O and formatting, you'll also see in this chapter how a really powerful C++ library can work.
2-2-2-1. Inserters and extractors▲
A stream is an object that transports and formats characters of a fixed width. You can have an input stream (via descendants of the istream class), an output stream (with ostream objects), or a stream that does both simultaneously (with objects derived from iostream). The iostreams library provides different types of such classes: ifstream,ofstream, and fstream for files, and istringstream, ostringstream, and stringstream for interfacing with the Standard C++ string class. All these stream classes have nearly identical interfaces, so you can use streams in a uniform manner, whether you're working with a file, standard I/O, a region of memory, or a string object. The single interface you learn also works for extensions added to support new classes. Some functions implement your formatting commands, and some functions read and write characters without formatting.
The stream classes mentioned earlier are actually template specializations,(41) much like the standard string class is a specialization of the basic_string template. The basic classes in the iostreams inheritance hierarchy are shown in the following figure:
The ios_base class declares everything that is common to all streams, independent of the type of character the stream handles. These declarations are mostly constants and functions to manage them, some of which you'll see throughout this chapter. The rest of the classes are templates that have the underlying character type as a parameter. The istream class, for example, is defined as follows:
typedef basic_istream<char> istream;All the classes mentioned earlier are defined via similar type definitions. There are also type definitions for all stream classes using wchar_t (the wide character type discussed in Chapter 3) instead of char. We'll look at these at the end of this chapter. The basic_ios template defines functions common to both input and output, but that depends on the underlying character type (we won't use these much). The template basic_istream defines generic functions for input, and basic_ostream does the same for output. The classes for file and string streams introduced later add functionality for their specific stream types.
In the iostreams library, two operators are overloaded to simplify the use of iostreams. The operator << is often referred to as an inserter for iostreams, and the operator >> is often referred to as an extractor.
Extractors parse the information that's expected by the destination object according to its type. To see an example of this, you can use the cin object, which is the iostream equivalent of stdin in C, that is, redirectable standard input. This object is predefined whenever you include the <iostream> header.
int i;
cin >> i;
float f;
cin >> f;
char c;
cin >> c;
char buf[100];
cin >> buf;There's an overloaded operator >> for every built-in data type. You can also overload your own, as you'll see later.
To find out what you have in the various variables, you can use the cout object (corresponding to standard output; there's also a cerr object corresponding to standard error) with the inserter <<:
cout << "i = ";
cout << i;
cout << "\n";
cout << "f = ";
cout << f;
cout << "\n";
cout << "c = ";
cout << c;
cout << "\n";
cout << "buf = ";
cout << buf;
cout << "\n";This is tedious and doesn't seem like much of an improvement over printf( ), despite improved type checking. Fortunately, the overloaded inserters and extractors are designed to be chained into a more complex expression that is much easier to write (and read):
cout << "i = " << i <<
endl;
cout << "f = " << f <<
endl;
cout << "c = " << c <<
endl;
cout << "buf = " << buf << endl;Defining inserters and extractors for your own classes is just a matter of overloading the associated operators to do the right things, namely:
- Make the first parameter a non-const reference to the stream (istream for input, ostream for output).
- Perform the operation by inserting/extracting data to/from the stream (by processing the components of the object).
- Return a reference to the stream.
The stream should be non-const because processing stream data changes the state of the stream. By returning the stream, you allow for chaining stream operations in a single statement, as shown earlier.
As an example, consider how to output the representation of a Date object in MM-DD-YYYY format. The following inserter does the job:
ostream& operator<<(ostream& os, const
Date& d) {
char fillc = os.fill('0');
os << setw(2) << d.getMonth() <<
'-'
<< setw(2) << d.getDay() << '-'
<< setw(4) << setfill(fillc) <<
d.getYear();
return os;
}This function cannot be a member of the Date class because the left operand of the << operator must be the output stream. The fill( ) member function of ostream changes the padding character used when the width of an output field, determined by the manipulatorsetw( ), is greater than needed for the data. We use a ‘0' character so that months preceding October will display a leading zero, such as “09” for September. The fill( ) function also returns the previous fill character (which defaults to a single space) so that we can restore it later with the manipulator setfill( ). We discuss manipulators in depth later in this chapter.
Extractors require a little more care because things can go wrong with input data. The way to signal a stream error is to set the stream's fail bit, as follows:
istream& operator>>(istream& is,
Date& d) {
is >> d.month;
char dash;
is >> dash;
if(dash != '-')
is.setstate(ios::failbit);
is >> d.day;
is >> dash;
if(dash != '-')
is.setstate(ios::failbit);
is >> d.year;
return is;
}When an error bit is set in a stream, all further streams operations are ignored until the stream is restored to a good state (explained shortly). That's why the code above continues extracting even if ios::failbit gets set. This implementation is somewhat forgiving in that it allows white space between the numbers and dashes in a date string (because the >> operator skips white space by default when reading built-in types). The following are valid date strings for this extractor:
"08-10-2003"
"8-10-2003"
"08 - 10 - 2003"but these are not:
"A-10-2003" // No alpha characters allowed
"08/2003" // Only
dashes allowed as a delimiterWe'll discuss stream state in more depth in the section “Handling stream errors” later in this chapter.
2-2-2-2. Common usage▲
As the Date extractor illustrated, you must be on guard for erroneous input. If the input produces an unexpected value, the process is skewed, and it's difficult to recover. In addition, formatted input defaults to white space delimiters. Consider what happens when we collect the code fragments from earlier in this chapter into a single program:
//: C04:Iosexamp.cpp {RunByHand}
// Iostream examples.
#include <iostream>
using namespace std;
int main() {
int i;
cin >> i;
float f;
cin >> f;
char c;
cin >> c;
char buf[100];
cin >> buf;
cout << "i = "
<< i << endl;
cout << "f = " << f <<
endl;
cout << "c = " << c <<
endl;
cout << "buf = " << buf
<< endl;
cout << flush;
cout << hex << "0x" << i
<< endl;
} ///:~and give it the following input:
12 1.4 c this is a testWe expect the same output as if we gave it
12
1.4
c
this is a testbut the output is, somewhat unexpectedly
i = 12
f = 1.4
c = c
buf = this
0xcNotice that buf got only the first word because the input routine looked for a space to delimit the input, which it saw after “this.” In addition, if the continuous input string is longer than the storage allocated for buf, we overrun the buffer.
In practice, you'll usually want to get input from interactive programs a line at a time as a sequence of characters, scan them, and then perform conversions once they're safely in a buffer. This way you don't need to worry about the input routine choking on unexpected data.
Another consideration is the whole concept of a command-line interface. This made sense in the past when the console was little more than a glass typewriter, but the world is rapidly changing to one where the graphical user interface (GUI) dominates. What is the meaning of console I/O in such a world? It makes much more sense to ignore cin altogether, other than for simple examples or tests, and take the following approaches:
- If your program requires input, read that input from a file—you'll soon see that it's remarkably easy to use files with iostreams. Iostreams for files still works fine with a GUI.
- Read the input without attempting to convert it, as we just suggested. When the input is some place where it can't foul things up during conversion, you can safely scan it.
- Output is different. If you're using a GUI, cout doesn't necessarily work, and you must send it to a file (which is identical to sending it to cout) or use the GUI facilities for data display. Otherwise it often makes sense to send it to cout. In both cases, the output formatting functions of iostreams are highly useful.
Another common practice saves compile time on large projects. Consider, for example, how you would declare the Date stream operators introduced earlier in the chapter in a header file. You only need to include the prototypes for the functions, so it's not really necessary to include the entire <iostream> header in Date.h. The standard practice is to only declare classes, something like this:
class ostream;This is an age-old technique for separating interface from implementation and is often called a forward declaration (and ostream at this point would be considered an incomplete type, since the class definition has not yet been seen by the compiler).
This will not work as is, however, for two reasons:
1. The stream classes are defined in the std namespace.
2. They are templates.
The proper declaration would be:
namespace std {
template<class charT, class traits =
char_traits<charT> >
class basic_ostream;
typedef basic_ostream<char> ostream;
}(As you can see, like the string class, the streams classes use the character traits classes mentioned in Chapter 3). Since it would be terribly tedious to type all that for every stream class you want to reference, the standard provides a header that does it for you: <iosfwd>. The Date header would then look something like this:
// Date.h
#include <iosfwd>
class Date {
friend std::ostream&
operator<<(std::ostream&,
const Date&);
friend std::istream&
operator>>(std::istream&, Date&);
// Etc.2-2-2-3. Line-oriented input▲
To grab input a line at a time, you have three choices:
- The member function get( )
- The member function getline( )
- The global function getline( ) defined in the <string> header
The first two functions take three arguments:
- A pointer to a character buffer in which to store the result.
- The size of that buffer (so it's not overrun).
- The terminating character, to know when to stop reading input.
The terminating character has a default value of '\n', which is what you'll usually use. Both functions store a zero in the result buffer when they encounter the terminating character in the input.
So what's the difference? Subtle, but important: get( ) stops when it sees the delimiter in the input stream, but it doesn't extract it from the input stream. Thus, if you did another get( ) using the same delimiter, it would immediately return with no fetched input. (Presumably, you either use a different delimiter in the next get( ) statement or a different input function.) The getline( ) function, on the other hand, extracts the delimiter from the input stream, but still doesn't store it in the result buffer.
The getline( ) function defined in <string> is convenient. It is not a member function, but rather a stand-alone function declared in the namespace std. It takes only two non-default arguments, the input stream and the string object to populate. Like its namesake, it reads characters until it encounters the first occurrence of the delimiter ('\n' by default) and consumes and discards the delimiter. The advantage of this function is that it reads into a string object, so you don't need to worry about buffer size.
Generally, when you're processing a text file that you read a line at a time, you'll want to use one of the getline( ) functions.
Overloaded versions of get( )
The get( ) function also comes in three other overloaded versions: one with no arguments that returns the next character using an int return value; one that stuffs a character into its char argument using a reference; and one that stores directly into the underlying buffer structure of another iostream object. The latter is explored later in the chapter.
Reading raw bytes
If you know exactly what you're dealing with and want to move the bytes directly into a variable, an array, or a structure in memory, you can use the unformatted I/O function read( ). The first argument for this function is a pointer to the destination memory, and the second is the number of bytes to read. This is especially useful if you've previously stored the information to a file, for example, in binary form using the complementary write( ) member function for an output stream (using the same compiler, of course). You'll see examples of all these functions later.
2-2-3. Handling stream errors▲
The Date extractor shown earlier sets a stream's fail bit under certain conditions. How does the user know when such a failure occurs? You can detect stream errors by either calling certain stream member functions to see if an error state has occurred, or if you don't care what the particular error was, you can just evaluate the stream in a Boolean context. Both techniques derive from the state of a stream's error bits.
Stream state
The ios_base class, from which ios derives,(42) defines four flags that you can use to test the state of a stream:
| Flag | Meaning |
| badbit | Some fatal (perhaps physical) error occurred. The stream should be considered unusable. |
| eofbit | End-of-input has occurred (either by encountering the physical end of a file stream or by the user terminating a console stream, such as with Ctrl-Z or Ctrl‑D). |
| failbit | An I/O operation failed, most likely because of invalid data (e.g., letters were found when trying to read a number). The stream is still usable. The failbit flag is also set when end-of-input occurs. |
| goodbit | All is well; no errors. End-of-input has not yet occurred. |
You can test whether any of these conditions have occurred by calling corresponding member functions that return a Boolean value indicating whether any of these have been set. The good( ) stream member function returns true if none of the other three bits are set. The eof( ) function returns true if eofbit is set, which happens with an attempt to read from a stream that has no more data (usually a file). Because end-of-input happens in C++ when trying to read past the end of the physical medium, failbit is also set to indicate that the “expected” data was not successfully read. The fail( ) function returns true if either failbit or badbit is set, and bad( ) returns true only if the badbit is set.
Once any of the error bits in a stream's state are set, they remain set, which is not always what you want. When reading a file, you might want to reposition to an earlier place in the file before end-of-file occurred. Just moving the file pointer doesn't automatically reset eofbit or failbit; you must do it yourself with the clear( ) function, like this:
myStream.clear(); // Clears all error bitsAfter calling clear( ), good( ) will return true if called immediately. As you saw in the Date extractor earlier, the setstate( ) function sets the bits you pass it. It turns out that setstate( ) doesn't affect any other bits—if they're already set, they stay set. If you want to set certain bits but at the same time reset all the rest, you can call an overloaded version of clear( ), passing it a bitwise expression representing the bits you want to set, as in:
myStream.clear(ios::failbit | ios::eofbit);Most of the time you won't be interested in checking the stream state bits individually. Usually you just want to know if everything is okay. This is the case when you read a file from beginning to end; you just want to know when the input data is exhausted. You can use a conversion function defined for void* that is automatically called when a stream occurs in a Boolean expression. Reading a stream until end-of-input using this idiom looks like the following:
int i;
while(myStream >> i)
cout << i <<
endl;Remember that operator>>( ) returns its stream argument, so the while statement above tests the stream as a Boolean expression. This particular example assumes that the input stream myStream contains integers separated by white space. The function ios_base::operator void*( ) simply calls good( ) on its stream and returns the result.(43) Because most stream operations return their stream, using this idiom is convenient.
Streams and exceptions
Iostreams existed as part of C++ long before there were exceptions, so checking stream state manually was just the way things were done. For backward compatibility, this is still the status quo, but modern iostreams can throw exceptions instead. The exceptions( ) stream member function takes a parameter representing the state bits for which you want exceptions to be thrown. Whenever the stream encounters such a state, it throws an exception of type std::ios_base::failure, which inherits from std::exception.
Although you can trigger a failure exception for any of the four stream states, it's not necessarily a good idea to enable exceptions for all of them. As Chapter 1 explains, use exceptions for truly exceptional conditions, but end-of-file is not only not exceptional—it's expected! For that reason, you might want to enable exceptions only for the errors represented by badbit, which you would do like this:
myStream.exceptions(ios::badbit);You enable exceptions on a stream-by-stream basis, since exceptions( ) is a member function for streams. The exceptions( ) function returns a bitmask(44) (of type iostate, which is some compiler-dependent type convertible to int) indicating which stream states will cause exceptions. If those states have already been set, an exception is thrown immediately. Of course, if you use exceptions in connection with streams, you had better be ready to catch them, which means that you need to wrap all stream processing with a try block that has an ios::failure handler. Many programmers find this tedious and just check states manually where they expect errors to occur (since, for example, they don't expect bad( ) to return true most of the time anyway). This is another reason that having streams throw exceptions is optional and not the default. In any case, you can choose how you want to handle stream errors. For the same reasons that we recommend using exceptions for error handling in other contexts, we do so here.
2-2-4. File iostreams▲
Manipulating files with iostreams is much easier and safer than using stdio in C. All you do to open a file is create an object—the constructor does the work. You don't need to explicitly close a file (although you can, using the close( ) member function) because the destructor will close it when the object goes out of scope. To create a file that defaults to input, make an ifstream object. To create one that defaults to output, make an ofstream object. An fstream object can do both input and output.
The file stream classes fit into the iostreams classes as shown in the following figure:
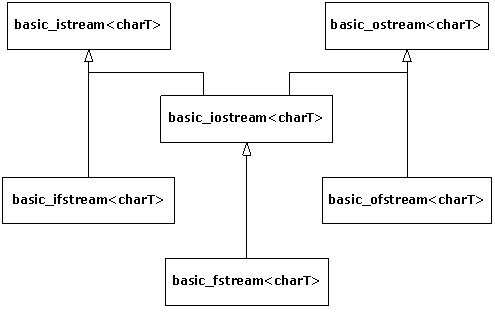
As before, the classes you actually use are template specializations defined by type definitions. For example, ifstream, which processes files of char, is defined as
typedef basic_ifstream<char> ifstream;2-2-4-1. A File-Processing Example▲
Here's an example that shows many of the features discussed so far. Notice the inclusion of <fstream>to declare the file I/O classes. Although on many platforms this will also include <iostream> automatically, compilers are not required to do so. If you want portable code, always include both headers.
//: C04:Strfile.cpp
// Stream I/O with files;
// The difference between get() & getline().
#include <fstream>
#include <iostream>
#include "../require.h"
using namespace std;
int main() {
const int SZ = 100; // Buffer size;
char buf[SZ];
{
ifstream in("Strfile.cpp"); // Read
assure(in, "Strfile.cpp"); // Verify open
ofstream out("Strfile.out"); // Write
assure(out, "Strfile.out");
int i = 1; // Line counter
// A less-convenient approach for line input:
while(in.get(buf, SZ)) { // Leaves \n in input
in.get(); // Throw away next character (\n)
cout << buf << endl; // Must add \n
// File output just like standard I/O:
out << i++ << ": " <<
buf << endl;
}
} // Destructors close in & out
ifstream in("Strfile.out");
assure(in, "Strfile.out");
// More convenient line input:
while(in.getline(buf, SZ)) { // Removes \n
char* cp = buf;
while(*cp != ':')
++cp;
cp += 2; // Past ": "
cout << cp << endl; // Must still add
\n
}
} ///:~The creation of both the ifstream and ofstream are followed by an assure( ) to guarantee the file was successfully opened. Here again the object, used in a situation where the compiler expects a Boolean result, produces a value that indicates success or failure.
The first while loop demonstrates the use of two forms of the get( ) function. The first gets characters into a buffer and puts a zero terminator in the buffer when either SZ-1 characters have been read or the third argument (defaulted to '\n') is encountered. The get( ) function leaves the terminator character in the input stream, so this terminator must be thrown away via in.get( ) using the form of get( ) with no argument, which fetches a single byte and returns it as an int. You can also use the ignore( ) member function, which has two default arguments. The first argument is the number of characters to throw away and defaults to one. The second argument is the character at which the ignore( ) function quits (after extracting it) and defaults to EOF.
Next, you see two output statements that look similar: one to cout and one to the file out. Notice the convenience here—you don't need to worry about the object type because the formatting statements work the same with all ostream objects. The first one echoes the line to standard output, and the second writes the line out to the new file and includes a line number.
To demonstrate getline( ), open the file we just created and strip off the line numbers. To ensure the file is properly closed before opening it to read, you have two choices. You can surround the first part of the program with braces to force the out object out of scope, thus calling the destructor and closing the file, which is done here. You can also call close( ) for both files; if you do this, you can even reuse the in object by calling the open( ) member function.
The second while loop shows how getline( ) removes the terminator character (its third argument, which defaults to '\n') from the input stream when it's encountered. Although getline( ), like get( ), puts a zero in the buffer, it still doesn't insert the terminating character.
This example, as well as most of the examples in this chapter, assumes that each call to any overload of getline( ) will encounter a newline character. If this is not the case, the eofbit state of the stream will be set and the call to getline( ) will return false, causing the program to lose the last line of input.
2-2-4-2. Open modes▲
You can control the way a file is opened by overriding the constructor's default arguments. The following table shows the flags that control the mode of the file:
| Flag | Function |
|---|---|
| ios::in | Opens an input file. Use this as an open mode for an ofstream to prevent truncating an existing file. |
| ios::out | Opens an output file. When used for an ofstream without ios::app, ios::ate or ios::in, ios::trunc is implied. |
| ios::app | Opens an output file for appending only. |
| ios::ate | Opens an existing file (either input or output) and seeks to the end. |
| ios::trunc | Truncates the old file if it already exists. |
| ios::binary | Opens a file in binary mode. The default is text mode. |
You can combine these flags using a bitwise or operation.
The binary flag, while portable, only has an effect on some non-UNIX systems, such as operating systems derived from MS-DOS, that have special conventions for storing end-of-line delimiters. For example, on MS-DOS systems in text mode (which is the default), every time you output a newline character ('\n'), the file system actually outputs two characters, a carriage-return/linefeed pair (CRLF), which is the pair of ASCII characters 0x0D and 0x0A. Conversely, when you read such a file back into memory in text mode, each occurrence of this pair of bytes causes a '\n' to be sent to the program in its place. If you want to bypass this special processing, you open files in binary mode. Binary mode has nothing whatsoever to do with whether you can write raw bytes to a file—you always can (by calling write( )) . You should, however, open a file in binary mode when you'll be using read( ) or write( ), because these functions take a byte count parameter. Having the extra '\r' characters will throw your byte count off in those instances. You should also open a file in binary mode if you're going to use the stream-positioning commands discussed later in this chapter.
You can open a file for both input and output by declaring an fstream object. When declaring an fstream object, you must use enough of the open mode flags mentioned earlier to let the file system know whether you want to input, output, or both. To switch from output to input, you need to either flush the stream or change the file position. To change from input to output, change the file position. To create a file via an fstream object, use the ios::trunc open mode flag in the constructor call to do both input and output.
2-2-5. Iostream buffering▲
Good design practice dictates that, whenever you create a new class, you should endeavor to hide the details of the underlying implementation as much as possible from the user of the class. You show them only what they need to know and make the rest private to avoid confusion. When using inserters and extractors, you normally don't know or care where the bytes are being produced or consumed, whether you're dealing with standard I/O, files, memory, or some newly created class or device.
A time comes, however, when it is important to communicate with the part of the iostream that produces and consumes bytes. To provide this part with a common interface and still hide its underlying implementation, the standard library abstracts it into its own class, called streambuf. Each iostream object contains a pointer to some kind of streambuf. (The type depends on whether it deals with standard I/O, files, memory, and so on.) You can access the streambuf directly; for example, you can move raw bytes into and out of the streambuf without formatting them through the enclosing iostream. This is accomplished by calling member functions for the streambuf object.
Currently, the most important thing for you to know is that every iostream object contains a pointer to a streambuf object, and the streambuf object has some member functions you can call if necessary. For file and string streams, there are specialized types of stream buffers, as the following figure illustrates:
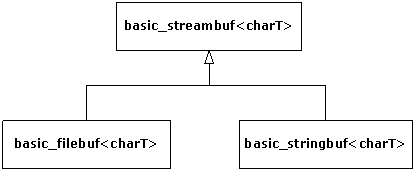
To allow you to access the streambuf, every iostream object has a member function called rdbuf( ) that returns the pointer to the object's streambuf. This way you can call any member function for the underlying streambuf. However, one of the most interesting things you can do with the streambuf pointer is to connect it to another iostream object using the << operator. This drains all the characters from your object into the one on the left side of the <<. If you want to move all the characters from one iostream to another, you don't need to go through the tedium (and potential coding errors) of reading them one character or one line at a time. This is a much more elegant approach.
Here's a simple program that opens a file and sends the contents to standard output (similar to the previous example):
//: C04:Stype.cpp
// Type a file to standard output.
#include <fstream>
#include <iostream>
#include "../require.h"
using namespace std;
int main() {
ifstream in("Stype.cpp");
assure(in, "Stype.cpp");
cout << in.rdbuf(); // Outputs entire file
} ///:~An ifstream is created using the source code file for this program as an argument. The assure( ) function reports a failure if the file cannot be opened. All the work really happens in the statement
cout << in.rdbuf();which sends the entire contents of the file to cout. This is not only more succinct to code, it is often more efficient than moving the bytes one at a time.
A form of get( ) writes directly into the streambuf of another object. The first argument is a reference to the destination streambuf, and the second is the terminating character (‘\n' by default), which stops the get( ) function. So there is yet another way to print a file to standard output:
//: C04:Sbufget.cpp
// Copies a file to standard output.
#include <fstream>
#include <iostream>
#include "../require.h"
using namespace std;
int main() {
ifstream in("Sbufget.cpp");
assure(in);
streambuf& sb = *cout.rdbuf();
while(!in.get(sb).eof()) {
if(in.fail()) // Found blank line
in.clear();
cout << char(in.get()); // Process '\n'
}
} ///:~The rdbuf( ) function returns a pointer, so it must be dereferenced to satisfy the function's need to see an object. Stream buffers are not meant to be copied (they have no copy constructor), so we define sb as a reference to cout's stream buffer. We need the calls to fail( ) and clear( ) in case the input file has a blank line (this one does). When this particular overloaded version of get( ) sees two newlines in a row (evidence of a blank line), it sets the input stream's fail bit, so we must call clear( ) to reset it so that the stream can continue to be read. The second call to get( ) extracts and echoes each newline delimiter. (Remember, the get( ) function doesn't extract its delimiter like getline( ) does.)
You probably won't need to use a technique like this often, but it's nice to know it exists.(45)
2-2-6. Seeking in iostreams▲
Each type of iostream has a concept of where its “next” character will come from (if it's an istream) or go (if it's an ostream). In some situations, you might want to move this stream position. You can do so using two models: one uses an absolute location in the stream called the streampos; the second works like the Standard C library functions fseek( ) for a file and moves a given number of bytes from the beginning, end, or current position in the file.
The streampos approach requires that you first call a “tell” function: tellp( ) for an ostream or tellg( ) for an istream. (The “p” refers to the “put pointer,” and the “g” refers to the “get pointer.”) This function returns a streampos you can later use in calls to seekp( ) for an ostream or seekg( ) for an istream when you want to return to that position in the stream.
The second approach is a relative seek and uses overloaded versions of seekp( ) and seekg( ). The first argument is the number of characters to move: it can be positive or negative. The second argument is the seek direction:
| ios::beg | From beginning of stream |
| ios::cur | Current position in stream |
| ios::end | From end of stream |
Here's an example that shows the movement through a file, but remember, you're not limited to seeking within files as you are with C's stdio. With C++, you can seek in any type of iostream (although the standard stream objects, such as cin and cout,explicitly disallow it):
//: C04:Seeking.cpp
// Seeking in iostreams.
#include <cassert>
#include <cstddef>
#include <cstring>
#include <fstream>
#include "../require.h"
using namespace std;
int main() {
const int STR_NUM = 5, STR_LEN = 30;
char origData[STR_NUM][STR_LEN] = {
"Hickory dickory dus. .
.",
"Are you tired of C++?",
"Well, if you have,",
"That's just too bad,",
"There's plenty more for us!"
};
char readData[STR_NUM][STR_LEN] = {{ 0
}};
ofstream
out("Poem.bin", ios::out | ios::binary);
assure(out, "Poem.bin");
for(int i = 0; i < STR_NUM; i++)
out.write(origData[i], STR_LEN);
out.close();
ifstream in("Poem.bin", ios::in |
ios::binary);
assure(in, "Poem.bin");
in.read(readData[0], STR_LEN);
assert(strcmp(readData[0], "Hickory dickory dus.
. .")
== 0);
// Seek -STR_LEN bytes from the end of file
in.seekg(-STR_LEN, ios::end);
in.read(readData[1], STR_LEN);
assert(strcmp(readData[1], "There's plenty more
for us!")
== 0);
// Absolute seek (like using operator[] with a file)
in.seekg(3 * STR_LEN);
in.read(readData[2], STR_LEN);
assert(strcmp(readData[2], "That's just too
bad,") == 0);
// Seek backwards from current position
in.seekg(-STR_LEN * 2, ios::cur);
in.read(readData[3], STR_LEN);
assert(strcmp(readData[3], "Well, if you
have,") == 0);
// Seek from the begining of the file
in.seekg(1 * STR_LEN, ios::beg);
in.read(readData[4], STR_LEN);
assert(strcmp(readData[4], "Are you tired of
C++?")
== 0);
} ///:~This program writes a poem to a file using a binary output stream. Since we reopen it as an ifstream, we use seekg( ) to position the “get pointer.” As you can see, you can seek from the beginning or end of the file or from the current file position. Obviously, you must provide a positive number to move from the beginning of the file and a negative number to move back from the end.
Now that you know about the streambuf and how to seek, you can understand an alternative method (besides using an fstream object) for creating a stream object that will both read and write a file. The following code first creates an ifstream with flags that say it's both an input and an output file. You can't write to an ifstream, so you need to create an ostream with the underlying stream buffer:
ifstream in("filename", ios::in | ios::out);
ostream out(in.rdbuf());You might wonder what happens when you write to one of these objects. Here's an example:
//: C04:Iofile.cpp
// Reading & writing one file.
#include <fstream>
#include <iostream>
#include "../require.h"
using namespace std;
int main() {
ifstream in("Iofile.cpp");
assure(in, "Iofile.cpp");
ofstream out("Iofile.out");
assure(out, "Iofile.out");
out << in.rdbuf(); // Copy file
in.close();
out.close();
// Open for reading and writing:
ifstream in2("Iofile.out", ios::in |
ios::out);
assure(in2, "Iofile.out");
ostream out2(in2.rdbuf());
cout << in2.rdbuf(); // Print whole file
out2 << "Where does this end up?";
out2.seekp(0, ios::beg);
out2 << "And what about this?";
in2.seekg(0, ios::beg);
cout << in2.rdbuf();
} ///:~The first five lines copy the source code for this program into a file called iofile.out and then close the files. This gives us a safe text file to play with. Then the aforementioned technique is used to create two objects that read and write to the same file. In cout << in2.rdbuf( ), you can see the “get” pointer is initialized to the beginning of the file. The “put” pointer, however, is set to the end of the file because “Where does this end up?” appears appended to the file. However, if the put pointer is moved to the beginning with a seekp( ), all the inserted text overwrites the existing text. Both writes are seen when the get pointer is moved back to the beginning with a seekg( ), and the file is displayed. The file is automatically saved and closed when out2 goes out of scope and its destructor is called.
2-2-7. String iostreams▲
A string stream works directly with memory instead of a file or standard output. It uses the same reading and formatting functions that you use with cin and cout to manipulate bytes in memory. On old computers, the memory was referred to as core, so this type of functionality is often called in-core formatting.
The class names for string streams echo those for file streams. If you want to create a string stream to extract characters from, you create an istringstream. If you want to put characters into a string stream, you create an ostringstream. All declarations for string streams are in the standard header <sstream>. As usual, there are class templates that fit into the iostreams hierarchy, as shown in the following figure:
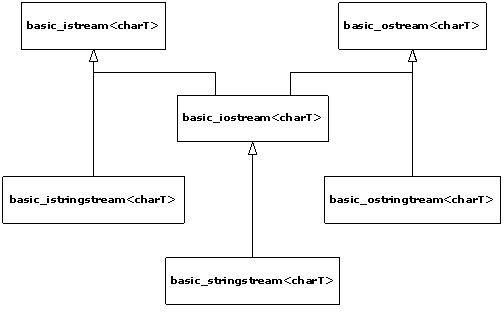
2-2-7-1. Input string streams▲
To read from a string using stream operations, you create an istringstream object initialized with the string. The following program shows how to use an istringstream object:
//: C04:Istring.cpp
// Input string streams.
#include <cassert>
#include <cmath> // For fabs()
#include <iostream>
#include <limits> // For epsilon()
#include <sstream>
#include <string>
using namespace std;
int main() {
istringstream s("47 1.414 This is a test");
int i;
double f;
s >> i >> f; // Whitespace-delimited
input
assert(i == 47);
double relerr = (fabs(f) - 1.414) / 1.414;
assert(relerr <=
numeric_limits<double>::epsilon());
string buf2;
s >> buf2;
assert(buf2 == "This");
cout << s.rdbuf(); // " is a test"
} ///:~You can see that this is a more flexible and general approach to transforming character strings to typed values than the standard C library functions such as atof( )or atoi( ), even though the latter may be more efficient for single conversions.
In the expression s >> i >> f, the first number is extracted into i, and the second into f. This isn't “the first whitespace-delimited set of characters” because it depends on the data type it's being extracted into. For example, if the string were instead, “1.414 47 This is a test,” then i would get the value 1 because the input routine would stop at the decimal point. Then f would get 0.414. This could be useful if you want to break a floating-point number into a whole number and a fraction part. Otherwise it would seem to be an error. The second assert( ) calculates the relative error between what we read and what we expected; it's always better to do this than to compare floating-point numbers for equality. The constant returned by epsilon( ), defined in <limits>, represents the machine epsilon for double-precision numbers, which is the best tolerance you can expect comparisons of doubles to satisfy.(46)
As you may already have guessed, buf2 doesn't get the rest of the string, just the next white-space-delimited word. In general, it's best to use the extractor in iostreams when you know the exact sequence of data in the input stream and you're converting to some type other than a character string. However, if you want to extract the rest of the string all at once and send it to another iostream, you can use rdbuf( ) as shown.
To test the Date extractor at the beginning of this chapter, we used an input string stream with the following test program:
//: C04:DateIOTest.cpp
//{L} ../C02/Date
#include <iostream>
#include <sstream>
#include "../C02/Date.h"
using namespace std;
void testDate(const string& s) {
istringstream os(s);
Date d;
os >> d;
if(os)
cout << d << endl;
else
cout << "input error with \""
<< s << "\"" << endl;
}
int main() {
testDate("08-10-2003");
testDate("8-10-2003");
testDate("08 - 10 - 2003");
testDate("A-10-2003");
testDate("08/2003");
} ///:~Each string literal in main( ) is passed by reference to testDate( ), which in turn wraps it in an istringstream so we can test thestream extractor we wrote for Date objects. The function testDate( ) also begins to test the inserter, operator<<( ).
2-2-7-2. Output string streams▲
To create an output string stream, you just create an ostringstream object, which manages a dynamically sized character buffer to hold whatever you insert. To get the formatted result as a string object, you call the str( ) member function. Here's an example:
//: C04:Ostring.cpp {RunByHand}
// Illustrates ostringstream.
#include <iostream>
#include <sstream>
#include <string>
using namespace std;
int main() {
cout << "type an int, a float and a
string: ";
int i;
float f;
cin >> i >> f;
cin >> ws; // Throw away
white space
string stuff;
getline(cin, stuff); // Get rest of the line
ostringstream os;
os << "integer = "
<< i << endl;
os << "float = " <<
f << endl;
os << "string = "
<< stuff << endl;
string result = os.str();
cout << result << endl;
} ///:~This is similar to the Istring.cpp example earlier that fetched an int and a float. A sample execution follows (the keyboard input is in bold type).
type an int, a float and a string: 10 20.5 the end
integer = 10
float = 20.5
string = the endYou can see that, like the other output streams, you can use the ordinary formatting tools, such as the << operator and endl, to send bytes to the ostringstream. The str( ) function returns a new string object every time you call it so the underlying stringbuf object owned by the string stream is left undisturbed.
In the previous chapter, we presented a program, HTMLStripper.cpp, that removed all HTML tags and special codes from a text file. As promised, here is a more elegant version using string streams.
//: C04:HTMLStripper2.cpp {RunByHand}
//{L} ../C03/ReplaceAll
// Filter to remove html tags and markers.
#include <cstddef>
#include <cstdlib>
#include <fstream>
#include <iostream>
#include <sstream>
#include <stdexcept>
#include <string>
#include "../C03/ReplaceAll.h"
#include "../require.h"
using namespace std;
string& stripHTMLTags(string& s)
throw(runtime_error) {
size_t leftPos;
while((leftPos = s.find('<')) != string::npos) {
size_t rightPos = s.find('>', leftPos+1);
if(rightPos == string::npos) {
ostringstream msg;
msg << "Incomplete HTML tag starting
in position "
<< leftPos;
throw runtime_error(msg.str());
}
s.erase(leftPos, rightPos - leftPos + 1);
}
// Remove all special HTML characters
replaceAll(s, "<",
"<");
replaceAll(s, ">",
">");
replaceAll(s, "&",
"&");
replaceAll(s, " ", " ");
// Etc...
return s;
}
int main(int argc, char* argv[]) {
requireArgs(argc, 1,
"usage: HTMLStripper2 InputFile");
ifstream in(argv[1]);
assure(in, argv[1]);
// Read entire file into string; then strip
ostringstream ss;
ss << in.rdbuf();
try {
string s = ss.str();
cout << stripHTMLTags(s) << endl;
return EXIT_SUCCESS;
} catch(runtime_error& x) {
cout << x.what() << endl;
return EXIT_FAILURE;
}
} ///:~In this program we read the entire file into a string by inserting a rdbuf( ) call to the file stream into an ostringstream. Now it's an easy matter to search for HTML delimiter pairs and erase them without having to worry about crossing line boundaries like we had to with the previous version in Chapter 3.
The following example shows how to use a bidirectional (that is, read/write) string stream:
//: C04:StringSeeking.cpp {-bor}{-dmc}
// Reads and writes a string stream.
#include <cassert>
#include <sstream>
#include <string>
using namespace std;
int main() {
string text = "We will hook no fish";
stringstream ss(text);
ss.seekp(0, ios::end);
ss << " before its time.";
assert(ss.str() ==
"We will hook no fish before its time.");
// Change "hook" to "ship"
ss.seekg(8, ios::beg);
string word;
ss >> word;
assert(word == "hook");
ss.seekp(8, ios::beg);
ss << "ship";
// Change "fish" to "code"
ss.seekg(16, ios::beg);
ss >> word;
assert(word == "fish");
ss.seekp(16, ios::beg);
ss << "code";
assert(ss.str() ==
"We will ship no code before its time.");
ss.str("A horse of a different color.");
assert(ss.str() == "A horse of a different
color.");
} ///:~As always, to move the put pointer, you call seekp( ), and to reposition the get pointer, you call seekg( ). Even though we didn't show it with this example, string streams are a little more forgiving than file streams in that you can switch from reading to writing or vice-versa at any time. You don't need to reposition the get or put pointers or flush the stream. This program also illustrates the overload of str( ) that replaces the stream's underlying stringbuf with a new string.
2-2-8. Output stream formatting▲
The goal of the iostreams design is to allow you to easily move and/or format characters. It certainly wouldn't be useful if you couldn't do most of the formatting provided by C's printf( ) family of functions. In this section, you'll learn all the output formatting functions that are available for iostreams, so you can format your bytes the way you want them.
The formatting functions in iostreams can be somewhat confusing at first because there's often more than one way to control the formatting: through both member functions and manipulators. To further confuse things, a generic member function sets state flags to control formatting, such as left or right justification, to use uppercase letters for hex notation, to always use a decimal point for floating-point values, and so on. On the other hand, separate member functions set and read values for the fill character, the field width, and the precision.
In an attempt to clarify all this, we'll first examine the internal formatting data of an iostream, along with the member functions that can modify that data. (Everything can be controlled through the member functions, if desired.) We'll cover the manipulators separately.
2-2-8-1. Format flags▲
The class ios contains data members to store all the formatting information pertaining to a stream. Some of this data has a range of values and is stored in variables: the floating-point precision, the output field width, and the character used to pad the output (normally a space). The rest of the formatting is determined by flags, which are usually combined to save space and are referred to collectively as the format flags. You can find out the value of the format flags with the ios::flags( ) member function, which takes no arguments and returns an object of type fmtflags (usually a synonym for long) that contains the current format flags. All the rest of the functions make changes to the format flags and return the previous value of the format flags.
fmtflags ios::flags(fmtflags newflags);
fmtflags ios::setf(fmtflags ored_flag);
fmtflags ios::unsetf(fmtflags
clear_flag);
fmtflags ios::setf(fmtflags bits, fmtflags field);The first function forces all the flags to change, which is sometimes what you want. More often, you change one flag at a time using the remaining three functions.
The use of setf( ) can seem somewhat confusing. To know which overloaded version to use, you must know what type of flag you're changing. There are two types of flags: those that are simply on or off, and those that work in a group with other flags. The on/off flags are the simplest to understand because you turn them on with setf(fmtflags) and off with unsetf(fmtflags). These flags are shown in the following table:
| on/off flag | Effect |
|---|---|
| ios::skipws | Skip white space. (For input; this is the default.) |
| ios::showbase | Indicate the numeric base (as set, for example, by dec, oct, or hex) when printing an integral value. Input streams also recognize the base prefix when showbase is on. |
| ios::showpoint | Show decimal point and trailing zeros for floating-point values. |
| ios::uppercase | Display uppercase A-F for hexadecimal values and E for scientific values. |
| ios::showpos | Show plus sign (+) for positive values. |
| ios::unitbuf | “Unit buffering.” The stream is flushed after each insertion. |
For example, to show the plus sign for cout, you say cout.setf(ios::showpos). To stop showing the plus sign, you say cout.unsetf(ios::showpos).
The unitbuf flag controls unit buffering, which means that each insertion is flushed to its output stream immediately. This is handy for error tracing, so that in case of a program crash, your data is still written to the log file. The following program illustrates unit buffering:
//: C04:Unitbuf.cpp {RunByHand}
#include <cstdlib> // For abort()
#include <fstream>
using namespace std;
int main() {
ofstream out("log.txt");
out.setf(ios::unitbuf);
out << "one" << endl;
out << "two" << endl;
abort();
} ///:~It is necessary to turn on unit buffering before any insertions are made to the stream. When we commented out the call to setf( ), one particular compiler had written only the letter ‘o' to the file log.txt. With unit buffering, no data was lost.
The standard error output stream cerr has unit buffering turned on by default. There is a cost for unit buffering, so if an output stream is heavily used, don't enable unit buffering unless efficiency is not a consideration.
2-2-8-2. Format fields▲
The second type of formatting flags work in a group. Only one of these flags can be set at a time, like the buttons on old car radios—you push one in, the rest pop out. Unfortunately this doesn't happen automatically, and you must pay attention to what flags you're setting so that you don't accidentally call the wrong setf( ) function. For example, there's a flag for each of the number bases: hexadecimal, decimal, and octal. Collectively, these flags are referred to as the ios::basefield. If the ios::dec flag is set and you call setf(ios::hex), you'll set the ios::hex flag, but you won't clear the ios::dec bit, resulting in undefined behavior. Instead, call the second form of setf( ) like this: setf(ios::hex, ios::basefield). This function first clears all the bits in the ios::basefield and then sets ios::hex. Thus, this form of setf( ) ensures that the other flags in the group “pop out” whenever you set one. The ios::hex manipulator does all this for you, automatically, so you don't need to concern yourself with the internal details of the implementation of this class or to even care that it's a set of binary flags. Later you'll see that there are manipulators to provide equivalent functionality in all the places you would use setf( ).
Here are the flag groups and their effects:
| ios::basefield | Effect |
|---|---|
| ios::dec | Format integral values in base 10 (decimal) (the default radix—no prefix is visible). |
| ios::hex | Format integral values in base 16 (hexadecimal). |
| ios::oct | Format integral values in base 8 (octal). |
| ios::floatfield | Effect |
|---|---|
| ios::scientific | Display floating-point numbers in scientific format. Precision field indicates number of digits after the decimal point. |
| ios::fixed | Display floating-point numbers in fixed format. Precision field indicates number of digits after the decimal point. |
| “automatic” (Neither bit is set.) | Precision field indicates the total number of significant digits. |
| ios::adjustfield | Effect |
|---|---|
| ios::left | Left-align values; pad on the right with the fill character. |
| ios::right | Right-align values. Pad on the left with the fill character. This is the default alignment. |
| ios::internal | Add fill characters after any leading sign or base indicator, but before the value. (In other words, the sign, if printed, is left-justified while the number is right-justified.) |
2-2-8-3. Width, fill, and precision▲
The internal variables that control the width of the output field, the fill character used to pad an output field, and the precision for printing floating-point numbers are read and written by member functions of the same name.
| Function | Effect |
|---|---|
| int ios::width( ) | Returns the current width. Default is 0. Used for both insertion and extraction. |
| int ios::width(int n) | Sets the width, returns the previous width. |
| int ios::fill( ) | Returns the current fill character. Default is space. |
| int ios::fill(int n) | Sets the fill character, returns the previous fill character. |
| int ios::precision( ) | Returns current floating-point precision. Default is 6. |
| int ios::precision(int n) | Sets floating-point precision, returns previous precision. See ios::floatfield table for the meaning of “precision.” |
The fill and precision values are fairly straightforward, but width requires some explanation. When the width is zero, inserting a value produces the minimum number of characters necessary to represent that value. A positive width means that inserting a value will produce at least as many characters as the width; if the value has fewer than width characters, the fill character pad the field. However, the value will never be truncated, so if you try to print 123 with a width of two, you'll still get 123. The field width specifies a minimum number of characters; there's no way to specify a maximum number.
The width is also distinctly different because it's reset to zero by each inserter or extractor that could be influenced by its value. It's really not a state variable, but rather an implicit argument to the inserters and extractors. If you want a constant width, call width( ) after each insertion or extraction.
2-2-8-4. An exhaustive example▲
To make sure you know how to call all the functions previously discussed, here's an example that calls them all:
//: C04:Format.cpp
// Formatting Functions.
#include <fstream>
#include <iostream>
#include "../require.h"
using namespace std;
#define D(A) T << #A << endl; A
int main() {
ofstream T("format.out");
assure(T);
D(int i = 47;)
D(float f = 2300114.414159;)
const char* s = "Is there any more?";
D(T.setf(ios::unitbuf);)
D(T.setf(ios::showbase);)
D(T.setf(ios::uppercase | ios::showpos);)
D(T << i << endl;) // Default is dec
D(T.setf(ios::hex, ios::basefield);)
D(T << i << endl;)
D(T.setf(ios::oct, ios::basefield);)
D(T << i << endl;)
D(T.unsetf(ios::showbase);)
D(T.setf(ios::dec, ios::basefield);)
D(T.setf(ios::left, ios::adjustfield);)
D(T.fill('0');)
D(T << "fill char: " <<
T.fill() << endl;)
D(T.width(10);)
T << i << endl;
D(T.setf(ios::right,
ios::adjustfield);)
D(T.width(10);)
T << i << endl;
D(T.setf(ios::internal,
ios::adjustfield);)
D(T.width(10);)
T << i << endl;
D(T << i << endl;)
// Without width(10)
D(T.unsetf(ios::showpos);)
D(T.setf(ios::showpoint);)
D(T << "prec = " <<
T.precision() << endl;)
D(T.setf(ios::scientific, ios::floatfield);)
D(T << endl << f << endl;)
D(T.unsetf(ios::uppercase);)
D(T << endl << f << endl;)
D(T.setf(ios::fixed, ios::floatfield);)
D(T << f << endl;)
D(T.precision(20);)
D(T << "prec = " <<
T.precision() << endl;)
D(T << endl << f << endl;)
D(T.setf(ios::scientific, ios::floatfield);)
D(T << endl << f << endl;)
D(T.setf(ios::fixed, ios::floatfield);)
D(T << f << endl;)
D(T.width(10);)
T << s << endl;
D(T.width(40);)
T << s << endl;
D(T.setf(ios::left, ios::adjustfield);)
D(T.width(40);)
T << s << endl;
} ///:~This example uses a trick to create a trace file so that you can monitor what's happening. The macro D(a) uses the preprocessor “stringizing” to turn a into a string to display. Then it reiterates a so the statement is executed. The macro sends all the information to a file called T, which is the trace file. The output is
int i = 47;
float f = 2300114.414159;
T.setf(ios::unitbuf);
T.setf(ios::showbase);
T.setf(ios::uppercase | ios::showpos);
T << i << endl;
+47
T.setf(ios::hex, ios::basefield);
T << i << endl;
0X2F
T.setf(ios::oct, ios::basefield);
T << i << endl;
057
T.unsetf(ios::showbase);
T.setf(ios::dec, ios::basefield);
T.setf(ios::left, ios::adjustfield);
T.fill('0');
T << "fill char: " << T.fill()
<< endl;
fill char: 0
T.width(10);
+470000000
T.setf(ios::right, ios::adjustfield);
T.width(10);
0000000+47
T.setf(ios::internal, ios::adjustfield);
T.width(10);
+000000047
T << i << endl;
+47
T.unsetf(ios::showpos);
T.setf(ios::showpoint);
T << "prec = " << T.precision()
<< endl;
prec = 6
T.setf(ios::scientific, ios::floatfield);
T << endl << f << endl;
2.300114E+06
T.unsetf(ios::uppercase);
T << endl << f << endl;
2.300114e+06
T.setf(ios::fixed, ios::floatfield);
T << f << endl;
2300114.500000
T.precision(20);
T << "prec = " << T.precision()
<< endl;
prec = 20
T << endl << f << endl;
2300114.50000000000000000000
T.setf(ios::scientific, ios::floatfield);
T << endl << f << endl;
2.30011450000000000000e+06
T.setf(ios::fixed, ios::floatfield);
T << f << endl;
2300114.50000000000000000000
T.width(10);
Is there any more?
T.width(40);
0000000000000000000000Is there any more?
T.setf(ios::left, ios::adjustfield);
T.width(40);
Is there any
more?0000000000000000000000Studying this output should clarify your understanding of the iostream formatting member functions.
2-2-9. Manipulators▲
As you can see from the previous program, calling the member functions for stream formatting operations can get a bit tedious. To make things easier to read and write, a set of manipulators is supplied to duplicate the actions provided by the member functions. Manipulators are a convenience because you can insert them for their effect within a containing expression; you don't need to create a separate function-call statement.
Manipulators change the state of the stream instead of (or in addition to) processing data. When you insert endl in an output expression, for example, it not only inserts a newline character, but it also flushes the stream (that is, puts out all pending characters that have been stored in the internal stream buffer but not yet output). You can also just flush a stream like this:
cout << flush;which causes a call to the flush( ) member function, as in:
cout.flush();as a side effect (nothing is inserted into the stream). Additional basic manipulators will change the number base to oct (octal), dec (decimal) or hex (hexadecimal):
cout << hex << "0x" << i << endl;In this case, numeric output will continue in hexadecimal mode until you change it by inserting either dec or oct in the output stream.
There's also a manipulator for extraction that “eats” white space:
cin >> ws;Manipulators with no arguments are provided in <iostream>. These include dec, oct, and hex, which perform the same action as, respectively, setf(ios::dec, ios::basefield), setf(ios::oct, ios::basefield), and setf(ios::hex, ios::basefield), albeit more succinctly. The <iostream> header also includes ws, endl, and flush and the additional set shown here:
| Manipulator | Effect |
|---|---|
| showbase noshowbase | Indicate the numeric base (dec, oct, or hex) when printing an integral value. |
|
showpos
noshowpos |
Show plus sign (+) for positive values. |
|
uppercase
nouppercase |
Display uppercase A-F for hexadecimal values, and display E for scientific values. |
|
showpoint
noshowpoint |
Show decimal point and trailing zeros for floating-point values. |
|
skipws
noskipws |
Skip white space on input. |
|
left
right internal |
Left-align, pad on right. Right-align, pad on left. Fill between leading sign or base indicator and value. |
|
scientific
fixed |
Indicates the display preference for floating-point output (scientific notation vs. fixed-point decimal). |
2-2-9-1. Manipulators with arguments▲
There are six standard manipulators, such as setw( ), that take arguments. These are defined in the header file <iomanip>, and are summarized in the following table:
| Manipulator | effect |
|---|---|
| setiosflags (fmtflags n) | Equivalent to a call to setf(n). The setting remains in effect until the next change, such as ios::setf( ). |
| resetiosflags (fmtflags n) | Clears only the format flags specified by n. The setting remains in effect until the next change, such as ios::unsetf( ). |
| setbase (base n) | Changes base to n, where n is 10, 8, or 16. (Anything else results in 0.) If n is zero, output is base 10, but input uses the C conventions: 10 is 10, 010 is 8, and 0xf is 15. You might as well use dec, oct, and hex for output. |
| setfill (char n) | Changes the fill character to n, such as ios::fill( ). |
| setprecision (int n) | Changes the precision to n, such as ios::precision( ). |
| setw(int n) | Changes the field width to n, such as ios::width( ). |
If you're doing a lot of formatting, you can see how using manipulators instead of calling stream member functions can clean up your code. As an example, here's the program from the previous section rewritten to use the manipulators. (The D( ) macro is removed to make it easier to read.)
//: C04:Manips.cpp
// Format.cpp using manipulators.
#include <fstream>
#include <iomanip>
#include <iostream>
using namespace std;
int main() {
ofstream trc("trace.out");
int i = 47;
float f = 2300114.414159;
char* s = "Is there any more?";
trc << setiosflags(ios::unitbuf
| ios::showbase | ios::uppercase
| ios::showpos);
trc << i << endl;
trc << hex << i <<
endl
<< oct << i <<
endl;
trc.setf(ios::left, ios::adjustfield);
trc << resetiosflags(ios::showbase)
<< dec << setfill('0');
trc << "fill char: " <<
trc.fill() << endl;
trc << setw(10) << i << endl;
trc.setf(ios::right, ios::adjustfield);
trc << setw(10) << i << endl;
trc.setf(ios::internal, ios::adjustfield);
trc << setw(10) << i << endl;
trc << i << endl; // Without setw(10)
trc << resetiosflags(ios::showpos)
<< setiosflags(ios::showpoint)
<< "prec = " <<
trc.precision() << endl;
trc.setf(ios::scientific, ios::floatfield);
trc << f << resetiosflags(ios::uppercase)
<< endl;
trc.setf(ios::fixed, ios::floatfield);
trc << f << endl;
trc << f << endl;
trc << setprecision(20);
trc << "prec = " <<
trc.precision() << endl;
trc << f << endl;
trc.setf(ios::scientific, ios::floatfield);
trc << f << endl;
trc.setf(ios::fixed, ios::floatfield);
trc << f << endl;
trc << f << endl;
trc << setw(10) << s << endl;
trc << setw(40) << s << endl;
trc.setf(ios::left, ios::adjustfield);
trc << setw(40) << s << endl;
} ///:~You can see that a lot of the multiple statements have been condensed into a single chained insertion. Notice the call to setiosflags( ) in which the bitwise-OR of the flags is passed. This could also have been done with setf( ) and unsetf( ) as in the previous example.
When using setw( ) with an output stream, the output expression is formatted into a temporary string that is padded with the current fill character if needed, as determined by comparing the length of the formatted result to the argument of setw( ). In other words, setw( ) affects the result string of a formatted output operation. Likewise, using setw( ) with input streams only is meaningful when reading strings, as the following example makes clear:
//: C04:InputWidth.cpp
// Shows limitations of setw with input.
#include <cassert>
#include <cmath>
#include <iomanip>
#include <limits>
#include <sstream>
#include <string>
using namespace std;
int main() {
istringstream is("one 2.34 five");
string temp;
is >> setw(2) >> temp;
assert(temp == "on");
is >> setw(2) >> temp;
assert(temp == "e");
double x;
is >> setw(2) >> x;
double relerr = fabs(x - 2.34) / x;
assert(relerr <=
numeric_limits<double>::epsilon());
} ///:~If you attempt to read a string, setw( ) will control the number of characters extracted quite nicely… up to a point. The first extraction gets two characters, but the second only gets one, even though we asked for two. That is because operator>>( ) uses white space as a delimiter (unless you turn off the skipws flag). When trying to read a number, however, such as x, you cannot use setw( ) to limit the characters read. With input streams, use only setw( ) for extracting strings.
2-2-9-2. Creating manipulators▲
Sometimes you'd like to create your own manipulators, and it turns out to be remarkably simple. A zero-argument manipulator such as endl is simply a function that takes as its argument an ostream reference and returns an ostream reference. The declaration for endl is
ostream& endl(ostream&);Now, when you say:
cout << "howdy" << endl;the endl produces the address of that function. So the compiler asks, “Is there a function that can be applied here that takes the address of a function as its argument?” Predefined functions in <iostream> do this; they're called applicators (because they apply a function to a stream). The applicator calls its function argument, passing it the ostream object as its argument. You don't need to know how applicators work to create your own manipulator; you only need to know that they exist. Here's the (simplified) code for an ostream applicator:
ostream& ostream::operator<<(ostream&
(*pf)(ostream&)) {
return pf(*this);
}The actual definition is a little more complicated since it involves templates, but this code illustrates the technique. When a function such as *pf (that takes a stream parameter and returns a stream reference) is inserted into a stream, this applicator function is called, which in turn executes the function to which pf points. Applicators for ios_base, basic_ios, basic_ostream, and basic_istream are predefined in the Standard C++ library.
To illustrate the process, here's a trivial example that creates a manipulator called nl that is equivalent to just inserting a newline into a stream (i.e., no flushing of the stream occurs, as with endl):
//: C04:nl.cpp
// Creating a manipulator.
#include <iostream>
using namespace std;
ostream& nl(ostream& os) {
return os << '\n';
}
int main() {
cout << "newlines" << nl
<< "between" << nl
<< "each" << nl <<
"word" << nl;
} ///:~When you insert nl into an output stream, such as cout, the following sequence of calls ensues:
cout.operator<<(nl) è nl(cout)The expression
os << '\n';inside nl( ) calls ostream::operator(char), which returns the stream, which is what is ultimately returned from nl( ).(47)
2-2-9-3. Effectors▲
As you've seen, zero-argument manipulators are easy to create. But what if you want to create a manipulator that takes arguments? If you inspect the <iomanip> header, you'll see a type called smanip, which is what the manipulators with arguments return. You might be tempted to somehow use that type to define your own manipulators, but don't do it. The smanip type is implementation-dependent and thus not portable. Fortunately, you can define such manipulators in a straightforward way without any special machinery, based on a technique introduced by Jerry Schwarz, called an effector.(48) An effector is a simple class whose constructor formats a string representing the desired operation, along with an overloaded operator<< to insert that string into a stream. Here's an example with two effectors. The first outputs a truncated character string, and the second prints a number in binary.
//: C04:Effector.cpp
// Jerry Schwarz's "effectors."
#include <cassert>
#include <limits> // For max()
#include <sstream>
#include <string>
using namespace std;
// Put out a prefix of a string:
class Fixw {
string str;
public:
Fixw(const string& s, int width) : str(s, 0,
width) {}
friend ostream& operator<<(ostream& os,
const Fixw& fw) {
return os << fw.str;
}
};
// Print a number in binary:
typedef unsigned long ulong;
class Bin {
ulong n;
public:
Bin(ulong nn) { n = nn; }
friend ostream& operator<<(ostream& os,
const Bin& b) {
const ulong ULMAX =
numeric_limits<ulong>::max();
ulong bit = ~(ULMAX >> 1); // Top bit set
while(bit) {
os << (b.n & bit ? '1' : '0');
bit >>= 1;
}
return os;
}
};
int main() {
string words = "Things that make us happy, make
us wise";
for(int i = words.size(); --i >= 0;) {
ostringstream s;
s << Fixw(words, i);
assert(s.str() == words.substr(0, i));
}
ostringstream xs, ys;
xs << Bin(0xCAFEBABEUL);
assert(xs.str() ==
"1100""1010""1111""1110""1011""1010""1011""1110");
ys << Bin(0x76543210UL);
assert(ys.str() ==
"0111""0110""0101""0100""0011""0010""0001""0000");
} ///:~The constructor for Fixw creates a shortened copy of its char* argument, and the destructor releases the memory created for this copy. The overloaded operator<< takes the contents of its second argument, the Fixw object, inserts it into the first argument, the ostream, and then returns the ostream so that it can be used in a chained expression. When you use Fixw in an expression like this:
cout << Fixw(string, i) << endl;a temporary object is created by the call to the Fixw constructor, and that temporary object is passed to operator<<. The effect is that of a manipulator with arguments. The temporary Fixw object persists until the end of the statement.
The Bin effector relies on the fact that shifting an unsigned number to the right shifts zeros into the high bits. We use numeric_limits<unsigned long>::max( ) (the largest unsigned long value, from the standard header <limits>) to produce a value with the high bit set, and this value is moved across the number in question (by shifting it to the right), masking each bit in turn. We've juxtaposed string literals in the code for readability; the separate strings are concatenated into a single string by the compiler.
Historically, the problem with this technique was that once you created a class called Fixw for char* or Bin for unsigned long,no one else could create a different Fixw or Bin class for their type. However, with namespaces, this problem is eliminated. Effectors and manipulators aren't equivalent, although they can often be used to solve the same problem. If you find that an effector isn't enough, you will need to conquer the complexity of manipulators.
2-2-10. Iostream examples▲
In this section you'll see examples that use what you've learned in this chapter. Although many tools exist to manipulate bytes (stream editors such as sed and awk from UNIX are perhaps the most well known, but a text editor also fits this category), they generally have some limitations. Both sed and awk can be slow and can only handle lines in a forward sequence, and text editors usually require human interaction, or at least learning a proprietary macro language. The programs you write with iostreams have none of these limitations: they're fast, portable, and flexible.
2-2-10-1. Maintaining class library source code▲
Generally, when you create a class, you think in library terms: you make a header file Name.h for the class declaration, and then create a file called Name.cpp where the member functions are implemented. These files have certain requirements: a particular coding standard (the program shown here uses the coding format for this book), and preprocessor statements surrounding the code in the header file to prevent multiple declarations of classes. (Multiple declarations confuse the compiler—it doesn't know which one you want to use. They could be different, so it throws up its hands and gives an error message.)
This example creates a new header/implementation pair of files or modifies an existing pair. If the files already exist, it checks and potentially modifies the files, but if they don't exist, it creates them using the proper format.
//: C04:Cppcheck.cpp
// Configures .h & .cpp files to conform to style
// standard. Tests existing files for conformance.
#include <fstream>
#include <sstream>
#include <string>
#include <cstddef>
#include "../require.h"
using namespace std;
bool startsWith(const string& base, const
string& key) {
return base.compare(0, key.size(), key) == 0;
}
void cppCheck(string fileName) {
enum bufs { BASE, HEADER, IMPLEMENT, HLINE1, GUARD1,
GUARD2, GUARD3, CPPLINE1, INCLUDE, BUFNUM };
string part[BUFNUM];
part[BASE] = fileName;
// Find any '.' in the string:
size_t loc = part[BASE].find('.');
if(loc != string::npos)
part[BASE].erase(loc); // Strip extension
// Force to upper case:
for(size_t i = 0; i < part[BASE].size(); i++)
part[BASE][i] = toupper(part[BASE][i]);
// Create file names and internal lines:
part[HEADER] = part[BASE] + ".h";
part[IMPLEMENT] = part[BASE] + ".cpp";
part[HLINE1] = "/" ": " +
part[HEADER];
part[GUARD1] = "ifndef " + part[BASE] +
"_H";
part[GUARD2] = "define " + part[BASE] +
"_H";
part[GUARD3] = "endif / " + part[BASE]
+"_H";
part[CPPLINE1] = string("/") + ":
" + part[IMPLEMENT];
part[INCLUDE] = "include \"" +
part[HEADER] + "\"";
// First, try to open existing files:
ifstream existh(part[HEADER].c_str()),
existcpp(part[IMPLEMENT].c_str());
if(!existh) { // Doesn't exist; create it
ofstream newheader(part[HEADER].c_str());
assure(newheader, part[HEADER].c_str());
newheader << part[HLINE1] << endl
<< part[GUARD1] << endl
<< part[GUARD2] << endl
<< endl
<< part[GUARD3] << endl;
} else { // Already exists; verify it
stringstream hfile; // Write & read
ostringstream newheader; // Write
hfile << existh.rdbuf();
// Check that first three lines conform:
bool changed = false;
string s;
hfile.seekg(0);
getline(hfile, s);
bool lineUsed = false;
// The call to good() is for Microsoft (later too):
for(int line = HLINE1; hfile.good() && line
<= GUARD2;
++line) {
if(startsWith(s, part[line])) {
newheader << s << endl;
lineUsed = true;
if(getline(hfile, s))
lineUsed = false;
} else {
newheader << part[line] << endl;
changed = true;
lineUsed = false;
}
}
// Copy rest of file
if(!lineUsed)
newheader << s << endl;
newheader << hfile.rdbuf();
// Check for GUARD3
string head = hfile.str();
if(head.find(part[GUARD3]) == string::npos) {
newheader << part[GUARD3] << endl;
changed = true;
}
// If there were changes, overwrite file:
if(changed) {
existh.close();
ofstream newH(part[HEADER].c_str());
assure(newH, part[HEADER].c_str());
newH << "//@//\n" // Change
marker
<< newheader.str();
}
}
if(!existcpp) { // Create cpp file
ofstream newcpp(part[IMPLEMENT].c_str());
assure(newcpp, part[IMPLEMENT].c_str());
newcpp << part[CPPLINE1] << endl
<< part[INCLUDE] << endl;
} else { // Already exists; verify it
stringstream cppfile;
ostringstream newcpp;
cppfile << existcpp.rdbuf();
// Check that first two lines conform:
bool changed = false;
string s;
cppfile.seekg(0);
getline(cppfile, s);
bool lineUsed = false;
for(int line = CPPLINE1;
cppfile.good() && line <= INCLUDE;
++line) {
if(startsWith(s, part[line])) {
newcpp << s << endl;
lineUsed = true;
if(getline(cppfile, s))
lineUsed = false;
} else {
newcpp << part[line] << endl;
changed = true;
lineUsed = false;
}
}
// Copy rest of file
if(!lineUsed)
newcpp << s << endl;
newcpp << cppfile.rdbuf();
// If there were changes, overwrite file:
if(changed) {
existcpp.close();
ofstream newCPP(part[IMPLEMENT].c_str());
assure(newCPP, part[IMPLEMENT].c_str());
newCPP << "//@//\n" // Change
marker
<< newcpp.str();
}
}
}
int main(int argc, char* argv[]) {
if(argc > 1)
cppCheck(argv[1]);
else
cppCheck("cppCheckTest.h");
} ///:~First notice the useful function startsWith( ), which does just what its name says—it returns true if the first string argument starts with the second argument. This is used when looking for the expected comments and include-related statements. Having the array of strings, part, allows for easy looping through the series of expected statements in source code. If the source file doesn't exist, we merely write the statements to a new file of the given name. If the file does exist, we search a line at a time, verifying that the expected lines occur. If they are not present, they are inserted. Special care must be taken to make sure we don't drop existing lines (see where we use the Boolean variable lineUsed). Notice that we use a stringstream for an existing file, so we can first write the contents of the file to it and then read from and search it.
The names in the enumeration are BASE, the capitalized base file name without extension; HEADER, the header file name; IMPLEMENT, the implementation file (cpp) name; HLINE1, the skeleton first line of the header file; GUARD1, GUARD2, and GUARD3, the “guard” lines in the header file (to prevent multiple inclusion); CPPLINE1, the skeleton first line of the cpp file; and INCLUDE, the line in the cpp file that includes the header file.
If you run this program without any arguments, the following two files are created:
// CPPCHECKTEST.h
#ifndef CPPCHECKTEST_H
#define CPPCHECKTEST_H
#endif // CPPCHECKTEST_H// CPPCHECKTEST.cpp
#include
"CPPCHECKTEST.h"(We removed the colon after the double-slash in the first comment lines so as not to confuse the book's code extractor. It will appear in the actual output produced by cppCheck.)
You can experiment by removing selected lines from these files and re-running the program. Each time you will see that the correct lines are added back in. When a file is modified, the string “//@//” is placed as the first line of the file to bring the change to your attention. You will need to remove this line before you process the file again (otherwise cppcheck will assume the initial comment line is missing).
2-2-10-2. Detecting compiler errors▲
All the code in this book is designed to compile as shown without errors. Lines of code that should generate a compile-time error may be commented out with the special comment sequence “//!”. The following program will remove these special comments and append a numbered comment to the line. When you run your compiler, it should generate error messages, and you will see all the numbers appear when you compile all the files. This program also appends the modified line to a special file so that you can easily locate any lines that don't generate errors.
//: C04:Showerr.cpp {RunByHand}
// Un-comment error generators.
#include <cstddef>
#include <cstdlib>
#include <cstdio>
#include <fstream>
#include <iostream>
#include <sstream>
#include <string>
#include "../require.h"
using namespace std;
const string USAGE =
"usage: showerr filename chapnum\n"
"where filename is a C++ source file\n"
"and chapnum is the chapter name it's
in.\n"
"Finds lines commented with //! and
removes\n"
"the comment, appending //(#) where # is
unique\n"
"across all files, so you can determine\n"
"if your compiler finds the error.\n"
"showerr /r\n"
"resets the unique counter.";
class Showerr {
const int CHAP;
const string MARKER, FNAME;
// File containing error number counter:
const string ERRNUM;
// File containing error lines:
const string ERRFILE;
stringstream edited; // Edited file
int counter;
public:
Showerr(const string& f, const string& en,
const string& ef, int c)
: CHAP(c), MARKER("//!"), FNAME(f),
ERRNUM(en),
ERRFILE(ef), counter(0) {}
void replaceErrors() {
ifstream infile(FNAME.c_str());
assure(infile, FNAME.c_str());
ifstream count(ERRNUM.c_str());
if(count) count >> counter;
int linecount = 1;
string buf;
ofstream errlines(ERRFILE.c_str(), ios::app);
assure(errlines, ERRFILE.c_str());
while(getline(infile, buf)) {
// Find marker at start of line:
size_t pos = buf.find(MARKER);
if(pos != string::npos) {
// Erase marker:
buf.erase(pos, MARKER.size() + 1);
// Append counter & error info:
ostringstream out;
out << buf << " / ("
<< ++counter << ") "
<< "Chapter " << CHAP
<< " File: " << FNAME
<< " Line " <<
linecount << endl;
edited << out.str();
errlines << out.str(); // Append error
file
}
else
edited << buf << "\n"; //
Just copy
++linecount;
}
}
void saveFiles() {
ofstream outfile(FNAME.c_str()); // Overwrites
assure(outfile, FNAME.c_str());
outfile << edited.rdbuf();
ofstream count(ERRNUM.c_str()); // Overwrites
assure(count, ERRNUM.c_str());
count << counter; // Save new counter
}
};
int main(int argc, char* argv[]) {
const string ERRCOUNT("../errnum.txt"),
ERRFILE("../errlines.txt");
requireMinArgs(argc, 1, USAGE.c_str());
if(argv[1][0] == '/' || argv[1][0] == '-') {
// Allow for other switches:
switch(argv[1][1]) {
case 'r': case 'R':
cout << "reset counter"
<< endl;
remove(ERRCOUNT.c_str()); // Delete files
remove(ERRFILE.c_str());
return EXIT_SUCCESS;
default:
cerr << USAGE << endl;
return EXIT_FAILURE;
}
}
if(argc == 3) {
Showerr s(argv[1], ERRCOUNT, ERRFILE, atoi(argv[2]));
s.replaceErrors();
s.saveFiles();
}
} ///:~You can replace the marker with one of your choice.
Each file is read a line at a time, and each line is searched for the marker appearing at the head of the line; the line is modified and put into the error line list and into the string stream, edited. When the whole file is processed, it is closed (by reaching the end of a scope), it is reopened as an output file, and edited is poured into the file. Also notice the counter is saved in an external file. The next time this program is invoked, it continues to increment the counter.
2-2-10-3. A simple data logger▲
This example shows an approach you might take to log data to disk and later retrieve it for processing. It is meant to produce a temperature-depth profile of the ocean at various points. The DataPoint class holds the data:
//: C04:DataLogger.h
// Datalogger record layout.
#ifndef DATALOG_H
#define DATALOG_H
#include <ctime>
#include <iosfwd>
#include <string>
using std::ostream;
struct Coord {
int deg, min, sec;
Coord(int d = 0, int m = 0, int s = 0)
: deg(d), min(m), sec(s) {}
std::string toString() const;
};
ostream& operator<<(ostream&, const
Coord&);
class DataPoint {
std::time_t timestamp; // Time & day
Coord latitude, longitude;
double depth, temperature;
public:
DataPoint(std::time_t ts, const Coord& lat,
const Coord& lon, double dep, double
temp)
: timestamp(ts), latitude(lat), longitude(lon),
depth(dep), temperature(temp) {}
DataPoint() : timestamp(0), depth(0), temperature(0)
{}
friend ostream& operator<<(ostream&,
const DataPoint&);
};
#endif // DATALOG_H ///:~A DataPoint consists of a time stamp, which is stored as a time_t value as defined in <ctime>, longitude and latitude coordinates, and values for depth and temperature. We use inserters for easy formatting. Here's the implementation file:
//: C04:DataLogger.cpp {O}
// Datapoint implementations.
#include "DataLogger.h"
#include <iomanip>
#include <iostream>
#include <sstream>
#include <string>
using namespace std;
ostream& operator<<(ostream& os, const
Coord& c) {
return os << c.deg << '*'
<< c.min << '\''
<< c.sec
<< '"';
}
string Coord::toString() const {
ostringstream os;
os << *this;
return os.str();
}
ostream& operator<<(ostream& os, const
DataPoint& d) {
os.setf(ios::fixed, ios::floatfield);
char fillc = os.fill('0'); // Pad on left with '0'
tm* tdata =
localtime(&d.timestamp);
os <<
setw(2) << tdata->tm_mon + 1 << '\\'
<< setw(2) <<
tdata->tm_mday << '\\'
<< setw(2) <<
tdata->tm_year+1900 << ' '
<< setw(2) << tdata->tm_hour
<< ':'
<< setw(2) <<
tdata->tm_min << ':'
<< setw(2) <<
tdata->tm_sec;
os.fill(' '); // Pad on left with ' '
streamsize prec = os.precision(4);
os << " Lat:" << setw(9)
<< d.latitude.toString()
<< ", Long:" << setw(9)
<< d.longitude.toString()
<< ", depth:" << setw(9)
<< d.depth
<< ", temp:" << setw(9)
<< d.temperature;
os.fill(fillc);
os.precision(prec);
return os;
} ///:~The Coord::toString( ) function is necessary because the DataPoint inserter calls setw( ) before it prints the latitude and longitude. If we used the stream inserter for Coord instead, the width would only apply to the first insertion (that is, to Coord::deg), since width changes are always reset immediately. The call to setf( ) causes the floating-point output to be fixed-precision, and precision( ) sets the number of decimal places to four. Notice how we restore the fill character and precision to whatever they were before the inserter was called.
To get the values from the time encoding stored in DataPoint::timestamp, we call the function std::localtime( ), which returns a static pointer to a tm object. The tm struct has the following layout:
struct tm {
int tm_sec; // 0-59 seconds
int tm_min; // 0-59 minutes
int tm_hour; // 0-23 hours
int tm_mday; // Day of month
int tm_mon; // 0-11 months
int tm_year; // Years since 1900
int tm_wday; // Sunday == 0, etc.
int tm_yday; // 0-365 day of year
int tm_isdst; // Daylight savings?
};Generating test data
Here's a program that creates a file of test data in binary form (using write( )) and a second file in ASCII form using the DataPoint inserter. You can also print it out to the screen, but it's easier to inspect in file form.
//: C04:Datagen.cpp
// Test data generator.
//{L} DataLogger
#include <cstdlib>
#include <ctime>
#include <cstring>
#include <fstream>
#include "DataLogger.h"
#include "../require.h"
using namespace std;
int main() {
time_t timer;
srand(time(&timer)); // Seed the random number
generator
ofstream data("data.txt");
assure(data, "data.txt");
ofstream bindata("data.bin", ios::binary);
assure(bindata, "data.bin");
for(int i = 0; i < 100; i++, timer += 55) {
// Zero to 199 meters:
double newdepth = rand() % 200;
double fraction = rand() % 100 + 1;
newdepth += 1.0 / fraction;
double newtemp = 150 + rand() % 200; // Kelvin
fraction = rand() % 100 + 1;
newtemp += 1.0 / fraction;
const DataPoint d(timer, Coord(45,20,31),
Coord(22,34,18), newdepth,
newtemp);
data << d << endl;
bindata.write(reinterpret_cast<const
char*>(&d),
sizeof(d));
}
} ///:~The file data.txt is created in the ordinary way as an ASCII file, but data.bin has the flag ios::binary to tell the constructor to set it up as a binary file. To illustrate the formatting used for the text file, here is the first line of data.txt (the line wraps because it's longer than this page will allow):
07\28\2003 12:54:40 Lat:45*20'31", Long:22*34'18", depth:
16.0164, temp: 242.0122The Standard C library function time( ) updates the time_t value its argument points to with an encoding of the current time, which on most platforms is the number of seconds elapsed since 00: 00: 00 GMT, January 1 1970 (the dawning of the age of Aquarius?). The current time is also a convenient way to seed the random number generator with the Standard C library function srand( ), as is done here.
After this, the timer is incremented by 55 seconds to give an interesting interval between readings in this simulation.
The latitude and longitude used are fixed values to indicate a set of readings at a single location. Both the depth and the temperature are generated with the Standard C library rand( ) function, which returns a pseudorandom number between zero and a platform-dependent constant, RAND_MAX, defined in <cstdlib> (usually the value of the platform's largest unsigned integer). To put this in a desired range, use the remainder operator % and the upper end of the range. These numbers are integral; to add a fractional part, a second call to rand( ) is made, and the value is inverted after adding one (to prevent divide-by-zero errors).
In effect, the data.bin file is being used as a container for the data in the program, even though the container exists on disk and not in RAM. write( ) sends the data out to the disk in binary form. The first argument is the starting address of the source block—notice it must be cast to a char* because that's what write( ) expects for narrow streams. The second argument is the number of characters to write, which in this case is the size of the DataPoint object (again, because we're using narrow streams). Because no pointers are contained in DataPoint, there is no problem in writing the object to disk. If the object is more sophisticated, you must implement a scheme for serialization, which writes the data referred to by pointers and defines new pointers when read back in later. (We don't talk about serialization in this volume—most vendor class libraries have some sort of serialization structure built into them.)
Verifying and viewing the data
To check the validity of the data stored in binary format, you can read it into memory with the read( ) member function for input streams, and compare it to the text file created earlier by Datagen.cpp. The following example just writes the formatted results to cout, but you can redirect this to a file and then use a file comparison utility to verify that it is identical to the original:
//: C04:Datascan.cpp
//{L} DataLogger
#include <fstream>
#include <iostream>
#include "DataLogger.h"
#include "../require.h"
using namespace std;
int main() {
ifstream bindata("data.bin", ios::binary);
assure(bindata, "data.bin");
DataPoint d;
while(bindata.read(reinterpret_cast<char*>(&d),
sizeof d))
cout << d << endl;
} ///:~2-2-11. Internationalization▲
The software industry is now a healthy, worldwide economic market, with demand for applications that can run in various languages and cultures. As early as the late 1980s, the C Standards Committee added support for non-U.S. formatting conventions with their locale mechanism. A locale is a set of preferences for displaying certain entities such as dates and monetary quantities. In the 1990s, the C Standards Committee approved an addendum to Standard C that specified functions to handle wide characters (denoted by the type wchar_t), which allow support for character sets other than ASCII and its commonly used Western European extensions. Although the size of a wide character is not specified, some platforms implement them as 32-bit quantities, so they can hold the encodings specified by the Unicode Consortium, as well as mappings to multi-byte characters sets defined by Asian standards bodies. C++ has integrated support for both wide characters and locales into the iostreams library.
2-2-11-1. Wide Streams▲
A wide stream is a stream class that handles wide characters. All the examples so far (except for the last traits example in Chapter 3) have used narrow streams that hold instances of char. Since stream operations are essentially the same no matter the underlying character type, they are encapsulated generically as templates. So all input streams, for example, are connected to the basic_istream class template:
template<class charT, class traits =
char_traits<charT> >
class basic_istream {...};In fact, all input stream types are specializations of this template, according to the following type definitions:
typedef basic_istream<char> istream;
typedef basic_istream<wchar_t> wistream;
typedef basic_ifstream<char> ifstream;
typedef basic_ifstream<wchar_t> wifstream;
typedef basic_istringstream<char> istringstream;
typedef
basic_istringstream<wchar_t> wistringstream;All other stream types are defined in similar fashion.
In a perfect world, this is all you'd need to create streams of different character types. But things aren't that simple. The reason is that the character-processing functions provided for char and wchar_t don't have the same names. To compare two narrow strings, for example, you use the strcmp( ) function. For wide characters, that function is named wcscmp( ). (Remember these originated in C, which does not have function overloading, hence unique names are required.) For this reason, a generic stream can't just call strcmp( ) in response to a comparison operator. There needs to be a way for the correct low-level functions to be called automatically.
The solution is to factor out the differences into a new abstraction. The operations you can perform on characters have been abstracted into the char_traits template, which has predefined specializations for char and wchar_t, as we discussed at the end of the previous chapter. To compare two strings, then, basic_string just calls traits::compare( ) (remember that traits is the second template parameter), which in turn calls either strcmp( ) or wcscmp( ), depending on which specialization is being used (transparent to basic_string).
You only need to be concerned about char_traits if you access the low-level character processing functions; most of the time you don't care. Consider, however, making your inserters and extractors more robust by defining them as templates, just in case someone wants to use them on a wide stream.
To illustrate, recall again the Date class inserter from the beginning of this chapter. We originally declared it as:
ostream& operator<<(ostream&, const Date&);This accommodates only narrow streams. To make it generic, we simply make it a template based on basic_ostream:
template<class charT, class traits>
std::basic_ostream<charT, traits>&
operator<<(std::basic_ostream<charT,
traits>& os,
const Date& d) {
charT fillc = os.fill(os.widen('0'));
charT dash = os.widen('-');
os << setw(2) << d.month << dash
<< setw(2) << d.day << dash
<< setw(4) << d.year;
os.fill(fillc);
return os;
}Notice that we also have to replace char with the template parameter charT in the declaration of fillc, since it could be either char or wchar_t, depending on the template instantiation being used.
Since you don't know when you're writing the template which type of stream you have, you need a way to automatically convert character literals to the correct size for the stream. This is the job of the widen( ) member function. The expression widen('-'), for example, converts its argument to L'-' (the literal syntax equivalent to the conversion wchar_t(‘-')) if the stream is a wide stream and leaves it alone otherwise. There is also a narrow( ) function that converts to a char if needed.
We can use widen( ) to write a generic version of the nl manipulator we presented earlier in the chapter.
template<class charT, class traits>
basic_ostream<charT,traits>&
nl(basic_ostream<charT,traits>& os) {
return os << charT(os.widen('\n'));
}2-2-11-2. Locales▲
Perhaps the most notable difference in typical numeric computer output from country to country is the punctuator used to separate the integer and fractional parts of a real number. In the United States, a period denotes a decimal point, but in much of the world, a comma is expected instead. It would be quite inconvenient to do all your own formatting for locale-dependent displays. Once again, creating an abstraction that handles these differences solves the problem.
That abstraction is the locale. All streams have an associated locale object that they use for guidance on how to display certain quantities for different cultural environments. A locale manages the categories of culture-dependent display rules, which are defined as follows:
| Category | Effect |
| collate | Allows comparing strings according to different, supported collating sequences. |
| ctype | Abstracts the character classification and conversion facilities found in <cctype>. |
| monetary | Supports different displays of monetary quantities. |
| numeric | Supports different display formats of real numbers, including radix (decimal point) and grouping (thousands) separators. |
| time | Supports various international formats for display of date and time. |
| messages | Scaffolding to implement context-dependent message catalogs (such as for error messages in different languages). |
The following program illustrates basic locale behavior:
//: C04:Locale.cpp {-g++}{-bor}{-edg} {RunByHand}
// Illustrates effects of locales.
#include <iostream>
#include <locale>
using namespace std;
int main() {
locale def;
cout << def.name() << endl;
locale current = cout.getloc();
cout << current.name() << endl;
float val = 1234.56;
cout << val << endl;
// Change to French/France
cout.imbue(locale("french"));
current = cout.getloc();
cout << current.name() << endl;
cout << val << endl;
cout << "Enter the literal 7890,12:
";
cin.imbue(cout.getloc());
cin >> val;
cout << val << endl;
cout.imbue(def);
cout << val << endl;
} ///:~Here's the output:
C
C
1234.56
French_France.1252
1234,56
Enter the literal 7890,12: 7890,12
7890,12
7890.12The default locale is the “C” locale, which is what C and C++ programmers have been used to all these years (basically, English language and American culture). All streams are initially “imbued” with the “C” locale. The imbue( ) member function changes the locale that a stream uses. Notice that the full ISO name for the “French” locale is displayed (that is, French used in France vs. French used in another country). This example shows that this locale uses a comma for a radix point in numeric display. We have to change cin to the same locale if we want to do input according to the rules of this locale.
Each locale category is divided into number of facets, which are classes encapsulating the functionality that pertains to that category. For example, the time category has the facets time_put and time_get, which contain functions for doing time and date input and output respectively. The monetary category has facets money_get, money_put, and moneypunct. (The latter facet determines the currency symbol.) The following program illustrates the moneypunct facet. (The time facet requires a sophisticated use of iterators which is beyond the scope of this chapter.)
//: C04:Facets.cpp {-bor}{-g++}{-mwcc}{-edg}
#include <iostream>
#include <locale>
#include <string>
using namespace std;
int main() {
// Change to French/France
locale loc("french");
cout.imbue(loc);
string currency =
use_facet<moneypunct<char>
>(loc).curr_symbol();
char point =
use_facet<moneypunct<char>
>(loc).decimal_point();
cout << "I made " << currency
<< 12.34 << " today!"
<< endl;
} ///:~The output shows the French currency symbol and decimal separator:
I made Ç12,34 today!You can also define your own facets to construct customized locales.(49) Be aware that the overhead for locales is considerable. In fact, some library vendors provide different “flavors” of the Standard C++ library to accommodate environments that have limited space.(50)
2-2-12. Summary▲
This chapter has given you a fairly thorough introduction to the iostream class library. What you've seen here is likely to be all you need to create programs using iostreams. However, be aware that some additional features in iostreams are not used often, but you can discover them by looking at the iostream header files and by reading your compiler's documentation on iostreams or the references mentioned in this chapter and in the appendices.
2-2-13. Exercises▲
Solutions to selected exercises can be found in the electronic document The Thinking in C++ Volume 2 Annotated Solution Guide, available for a small fee from www.MindView.net.
- Open a file by creating an ifstream object. Make an ostringstream object and read the entire contents into the ostringstream using the rdbuf( ) member function. Extract a string copy of the underlying buffer and capitalize every character in the file using the Standard C toupper( ) macro defined in <cctype>. Write the result out to a new file.
- Create a program that opens a file (the first argument on the command line) and searches it for any one of a set of words (the remaining arguments on the command line). Read the input a line at a time, and write out the lines (with line numbers) that match to the new file.
- Write a program that adds a copyright notice to the beginning of all source-code files indicated by the program's command-line arguments.
- Use your favorite text-searching program (grep, for example) to output the names (only) of all the files that contain a particular pattern. Redirect the output into a file. Write a program that uses the contents of that file to generate a batch file that invokes your editor on each of the files found by the search program.
- We know that setw( ) allows for a minimum of characters read in, but what if you wanted to read a maximum? Write an effector that allows the user to specify a maximum number of characters to extract. Have your effector also work for output, in such a way that output fields are truncated, if necessary, to stay within width limits.
- Demonstrate to yourself that if the fail or bad bit is set, and you subsequently turn on stream exceptions, that the stream will immediately throw an exception.
- String streams accommodate easy conversions, but they come with a price. Write a program that races atoi( ) against the stringstream conversion system to see the effect of the overhead involved with stringstream.
- Make a Person struct with fields such as name, age,
address, etc. Make the string fields fixed-size arrays. The social security
number will be the key for each record. Implement the following Database
class:
Sélectionnez
classDataBase{public:// Find where a record is on disksize_t query(size_t ssn);// Return the person at rn (record number)Person retrieve(size_t rn);// Record a record on diskvoidadd(constPerson&p);}; - Write some Person records to disk (do not keep them all in memory). When the user requests a record, read it off the disk and return it. The I/O operations in the DataBase class use read( ) and write( ) to process all Person records.
- Write an operator<< inserter for the Person struct that can be used to display records in a format for easy reading. Demonstrate it by writing data out to a file.
- Suppose the database for your Person structs was lost but that you have the file you wrote from the previous exercise. Recreate your database using this file. Be sure to use error checking.
- Write size_t(-1) (the largest unsigned int on your platform) to a text file 1,000,000 times. Repeat, but write to a binary file. Compare the size of the two files, and see how much room is saved using the binary format. (You may first want to calculate how much will be saved on your platform.)
- Discover the maximum number of digits of precision your implementation of iostreams will print by repeatedly increasing the value of the argument to precision( ) when printing a transcendental number such as sqrt(2.0).
- Write a program that reads real numbers from a file and prints their sum, average, minimum, and maximum.
- Determine the output of the following program before it is
executed:
Sélectionnez
//: C04:Exercise14.cpp#include<fstream>#include<iostream>#include<sstream>#include"../require.h"usingnamespacestd;#define d(a) cout << #a" ==\t"<<a<<endl;voidtellPointers(fstream&s){d(s.tellp()); d(s.tellg()); cout<<endl;}voidtellPointers(stringstream&s){d(s.tellp()); d(s.tellg()); cout<<endl;}intmain(){fstream in("Exercise14.cpp"); assure(in,"Exercise14.cpp"); in.seekg(10); tellPointers(in); in.seekp(20); tellPointers(in); stringstream memStream("Here is asentence."); memStream.seekg(10); tellPointers(memStream); memStream.seekp(5); tellPointers(memStream);}///:~ - Suppose you are given line-oriented data in a file formatted as
follows:
Sélectionnez
//: C04:Exercise15.txtAustralia5E56,7667230284,Langler,Tyson,31.2147,0.000421173612B97,7586701,Oneill,Zeke,553.429,0.00746730531560654D75,7907252710,Nickerson,Kelly,761.612,0.0102762769F2,6882945012,Hartenbach,Neil,47.9637,0.0006471644Austria480F,7187262472,Oneill,Dee,264.012,0.003562260400131B65,4754732628,Haney,Kim,7.33843,0.000099015948475DA1,1954960784,Pascente,Lester,56.5452,0.00076295293F18,1839715659,Elsea,Chelsy,801.901,0.010819887645Belgium BDF,5993489554,Oneill,Meredith,283.404,0.00382391275AC6,6612945602,Parisienne,Biff,557.74,0.00752547276AD,6477082,Pennington,Lizanne,31.0807,0.00041935444D0E,7861652688,Sisca,Francis,704.751,0.00950906238Bahamas37D8,6837424208,Parisienne,Samson,396.104,0.00534455E98,6384069,Willis,Pam,90.4257,0.001220095640592461462,1288616408,Stover,Hazal,583.939,0.0078789705615FF3,8028775718,Stromstedt,Bunk,39.8712,0.0005379741095,3737212,Stover,Denny,3.05387,0.0000412052488837428,2019381883,Parisienne,Shane,363.272,0.00490155///:~The heading of each section is a region, and every line under that heading is a seller in that region. Each comma-separated field represents the data about each seller. The first field in a line is the SELLER_ID which unfortunately was written out in hexadecimal format. The second is the PHONE_NUMBER (notice that some are missing area codes). LAST_NAME and FIRST_NAME then follow. TOTAL_SALES is the second to the last column. The last column is the decimal amount of the total sales that the seller represents for the company. You are to format the data on the terminal window so that an executive can easily interpret the trends. Sample output is given below.
Australia
---------------------------------
*Last Name* *First Name* *ID* *Phone* *Sales* *Percent*
Langler Tyson 24150 766-723-0284 31.24 4.21E-02
Oneill Zeke 11159 XXX-758-6701 553.43 7.47E-01
(etc.)
2-3. Templates in Depth▲
The C++ template facility goes far beyond simple “containers of T.” Although the original motivation was to enable type-safe, generic containers, in modern C++, templates are also used to generate custom code and to optimize program execution through compile-time programming constructs.
In this chapter we offer a practical look at the power (and pitfalls) of programming with templates in modern C++. For a more complete analysis of template-related language issues and pitfalls, we recommend the superb book by Daveed Vandevoorde and Nico Josuttis.(51)
2-3-1. Template parameters▲
As illustrated in Volume 1, templates come in two flavors: function templates and class templates. Both are wholly characterized by their parameters. Each template parameter can represent one of the following:
1. Types (either built-in or user-defined).
2. Compile-time constant values (for example, integers, and pointers and references to static entities; often referred to as non-type parameters).
3. Other templates.
The examples in Volume 1 all fall into the first category and are the most common. The canonical example for simple container-like templates nowadays seems to be a Stack class. Being a container, a Stack object is not concerned with the type of object it stores; the logic of holding objects is independent of the type of objects being held. For this reason you can use a type parameter to represent the contained type:
template<class T> class Stack {
T* data;
size_t count;
public:
void push(const T& t);
// Etc.
};The actual type to be used for a particular Stack instance is determined by the argument for the parameter T:
Stack<int> myStack; // A Stack of intsThe compiler then provides an int-version of Stack by substituting int for T and generating the corresponding code. The name of the class instance generated from the template in this case is Stack<int>.
2-3-1-1. Non-type template parameters▲
A non-type template parameter must be an integral value that is known at compile time. You can make a fixed-size Stack, for instance, by specifying a non-type parameter to be used as the dimension for the underlying array, as follows.
template<class T, size_t N> class Stack {
T data[N]; // Fixed capacity is N
size_t count;
public:
void push(const T& t);
// Etc.
};You must provide a compile-time constant value for the parameter N when you request an instance of this template, such as
Stack<int, 100> myFixedStack;Because the value of N is known at compile time, the underlying array (data) can be placed on the runtime stack instead of on the free store. This can improve runtime performance by avoiding the overhead associated with dynamic memory allocation. Following the pattern mentioned earlier, the name of the class above is Stack<int, 100>. This means that each distinct value of N results in a unique class type. For example, Stack<int, 99> is a distinct class from Stack<int, 100>.
The bitset class template, discussed in detail in Chapter 7, is the only class in the Standard C++ library that uses a non-type template parameter (which specifies the number of bits the bitset object can hold). The following random number generator example uses a bitset to track numbers so all the numbers in its range are returned in random order without repetition before starting over. This example also overloads operator( ) to produce a familiar function-call syntax.
//: C05:Urand.h {-bor}
// Unique randomizer.
#ifndef URAND_H
#define URAND_H
#include <bitset>
#include <cstddef>
#include <cstdlib>
#include <ctime>
using std::size_t;
using std::bitset;
template<size_t UpperBound> class Urand {
bitset<UpperBound> used;
public:
Urand() { srand(time(0)); } // Randomize
size_t operator()(); // The "generator"
function
};
template<size_t UpperBound>
inline size_t Urand<UpperBound>::operator()() {
if(used.count() == UpperBound)
used.reset(); // Start over (clear bitset)
size_t newval;
while(used[newval = rand() % UpperBound])
; // Until unique value is found
used[newval] = true;
return newval;
}
#endif // URAND_H ///:~The numbers generated by Urand are unique because the bitset used tracks all the possible numbers in the random space (the upper bound is set with the template argument) and records each used number by setting the corresponding position bit. When the numbers are all used up, the bitset is cleared to start over. Here's a simple driver that illustrates how to use a Urand object:
//: C05:UrandTest.cpp {-bor}
#include <iostream>
#include "Urand.h"
using namespace std;
int main() {
Urand<10> u;
for(int i = 0; i < 20; ++i)
cout << u() << ' ';
} ///:~As we explain later in this chapter, non-type template arguments are also important in the optimization of numeric computations.
2-3-1-2. Default template arguments▲
You can provide default arguments for template parameters in class templates, but not function templates. As with default function arguments, they should only be defined once, the first time a template declaration or definition is seen by the compiler. Once you introduce a default argument, all the subsequent template parameters must also have defaults. To make the fixed-size Stack template shown earlier a little friendlier, for example, you can add a default argument like this:
template<class T, size_t N = 100> class Stack {
T data[N]; // Fixed capacity is N
size_t count;
public:
void push(const T& t);
// Etc.
};Now, if you omit the second template argument when declaring a Stack object, the value for N will default to 100.
You can choose to provide defaults for all arguments, but you must use an empty set of brackets when declaring an instance so that the compiler knows that a class template is involved:
template<class T = int, size_t N = 100> // Both
defaulted
class Stack {
T data[N]; // Fixed capacity is N
size_t count;
public:
void push(const T& t);
// Etc.
};
Stack<> myStack; // Same as Stack<int, 100>Default arguments are used heavily in the Standard C++ library. The vector class template, for instance, is declared as follows:
template<class T, class Allocator =
allocator<T> >
class vector;Note the space between the last two right angle bracket characters. This prevents the compiler from interpreting those two characters (>>) as the right-shift operator.
This declaration reveals that vector takes two arguments: the type of the contained objects it holds, and a type that represents the allocator used by the vector. Whenever you omit the second argument, the standard allocator template is used, parameterized by the first template parameter. This declaration also shows that you can use template parameters in subsequent template parameters, as T is used here.
Although you cannot use default template arguments in function templates, you can use template parameters as default arguments to normal functions. The following function template adds the elements in a sequence:
//: C05:FuncDef.cpp
#include <iostream>
using namespace std;
template<class T> T sum(T* b, T* e, T init = T())
{
while(b != e)
init += *b++;
return init;
}
int main() {
int a[] = { 1, 2, 3 };
cout << sum(a, a + sizeof a / sizeof a[0])
<< endl; // 6
} ///:~The third argument to sum( ) is the initial value for the accumulation of the elements. Since we omitted it, this argument defaults to T( ), which in the case of int and other built-in types invokes a pseudo-constructor that performs zero-initialization.
2-3-1-3. Template template parameters▲
The third type of parameter a template can accept is another class template. If you are going to use a template type parameter itself as a template in your code, the compiler needs to know that the parameter is a template in the first place. The following example illustrates a template template parameter:
//: C05:TempTemp.cpp
// Illustrates a template template parameter.
#include <cstddef>
#include <iostream>
using namespace std;
template<class T>
class Array { // A simple, expandable sequence
enum { INIT = 10 };
T* data;
size_t capacity;
size_t count;
public:
Array() {
count = 0;
data = new T[capacity = INIT];
}
~Array() { delete [] data; }
void push_back(const T& t) {
if(count == capacity) {
// Grow underlying array
size_t newCap = 2 * capacity;
T* newData = new T[newCap];
for(size_t i = 0; i < count; ++i)
newData[i] = data[i];
delete [] data;
data = newData;
capacity = newCap;
}
data[count++] = t;
}
void pop_back() {
if(count > 0)
--count;
}
T* begin() { return data; }
T* end() { return data + count; }
};
template<class T,
template<class> class Seq>
class Container {
Seq<T> seq;
public:
void append(const T& t) { seq.push_back(t); }
T* begin() { return seq.begin(); }
T* end() { return seq.end(); }
};
int main() {
Container<int, Array> container;
container.append(1);
container.append(2);
int* p = container.begin();
while(p != container.end())
cout << *p++ << endl;
} ///:~The Array class template is a trivial sequence container. The Container template takes two parameters: the type that it holds, and a sequence data structure to do the holding. The following line in the implementation of the Container class requires that we inform the compiler that Seq is a template:
Seq<T> seq;If we hadn't declared Seq to be a template template parameter, the compiler would complain here that Seq is not a template, since we're using it as such. In main( ) a Container is instantiated to use an Array to hold integers, so Seq stands for Array in this example.
Note that it is not necessary in this case to name the parameter for Seq inside Container's declaration. The line in question is:
template<class T, template<class> class Seq>Although we could have written
template<class T, template<class U> class Seq>the parameter U is not needed anywhere. All that matters is that Seq is a class template that takes a single type parameter. This is analogous to omitting the names of function parameters when they're not needed, such as when you overload the post-increment operator:
T operator++(int);The int here is merely a placeholder and so needs no name.
The following program uses a fixed-size array, which has an extra template parameter representing the array length:
//: C05:TempTemp2.cpp
// A multi-variate template template
parameter.
#include <cstddef>
#include <iostream>
using namespace std;
template<class T, size_t N> class Array {
T data[N];
size_t count;
public:
Array() { count = 0; }
void push_back(const T& t) {
if(count < N)
data[count++] = t;
}
void pop_back() {
if(count > 0)
--count;
}
T* begin() { return data; }
T* end() { return data + count; }
};
template<class T,size_t
N,template<class,size_t> class Seq>
class Container {
Seq<T,N> seq;
public:
void append(const T& t) { seq.push_back(t); }
T* begin() { return seq.begin(); }
T* end() { return seq.end(); }
};
int main() {
const size_t N = 10;
Container<int, N, Array> container;
container.append(1);
container.append(2);
int* p = container.begin();
while(p != container.end())
cout << *p++ << endl;
} ///:~Once again, parameter names are not needed in the declaration of Seq inside Container's declaration, but we need two parameters to declare the data member seq, hence the appearance of the non-type parameter N at the top level.
Combining default arguments with template template parameters is slightly more problematic. When the compiler looks at the inner parameters of a template template parameter, default arguments are not considered, so you have to repeat the defaults in order to get an exact match. The following example uses a default argument for the fixed-size Array template and shows how to accommodate this quirk in the language:
//: C05:TempTemp3.cpp {-bor}{-msc}
// Template template parameters and default arguments.
#include <cstddef>
#include <iostream>
using namespace std;
template<class T, size_t N = 10> // A default
argument
class Array {
T data[N];
size_t count;
public:
Array() { count = 0; }
void push_back(const T& t) {
if(count < N)
data[count++] = t;
}
void pop_back() {
if(count > 0)
--count;
}
T* begin() { return data; }
T* end() { return data + count; }
};
template<class T, template<class, size_t = 10>
class Seq>
class Container {
Seq<T> seq; // Default used
public:
void append(const T& t) { seq.push_back(t); }
T* begin() { return seq.begin(); }
T* end() { return seq.end(); }
};
int main() {
Container<int, Array> container;
container.append(1);
container.append(2);
int* p = container.begin();
while(p != container.end())
cout << *p++ << endl;
} ///:~The default dimension of 10 is required in the line:
template<class T, template<class, size_t = 10> class Seq>Both the definition of seq in Container and container in main( ) use the default. The only way to use something other than the default value was shown in TempTemp2.cpp. This is the only exception to the rule stated earlier that default arguments should appear only once in a compilation unit.
Since the standard sequence containers (vector, list, and deque, discussed in depth in Chapter 7) have a default allocator argument, the technique shown above is helpful should you ever want to pass one of these sequences as a template parameter. The following program passes a vector and then a list to two instances of Container:
//: C05:TempTemp4.cpp {-bor}{-msc}
// Passes standard sequences as template arguments.
#include <iostream>
#include <list>
#include <memory> // Declares allocator<T>
#include <vector>
using namespace std;
template<class T,
template<class U, class = allocator<U> >
class Seq>
class Container {
Seq<T> seq; // Default of allocator<T>
applied implicitly
public:
void push_back(const T& t) { seq.push_back(t); }
typename Seq<T>::iterator begin() { return
seq.begin(); }
typename Seq<T>::iterator end() { return
seq.end(); }
};
int main() {
// Use a vector
Container<int, vector> vContainer;
vContainer.push_back(1);
vContainer.push_back(2);
for(vector<int>::iterator p = vContainer.begin();
p != vContainer.end();
++p) {
cout << *p <<
endl;
}
// Use a list
Container<int, list> lContainer;
lContainer.push_back(3);
lContainer.push_back(4);
for(list<int>::iterator p2 = lContainer.begin();
p2 != lContainer.end(); ++p2) {
cout << *p2 << endl;
}
} ///:~Here we name the first parameter of the inner template Seq (with the name U) because the allocators in the standard sequences must themselves be parameterized with the same type as the contained objects in the sequence. Also, since the default allocator parameter is known, we can omit it in the subsequent references to Seq<T>, as we did in the previous program. To fully explain this example, however, we have to discuss the semantics of the typename keyword.
2-3-1-4. The typename keyword▲
Consider the following:
//: C05:TypenamedID.cpp {-bor}
// Uses 'typename' as a prefix for nested types.
template<class T> class X {
// Without typename, you should get an error:
typename T::id i;
public:
void f() { i.g(); }
};
class Y {
public:
class id {
public:
void g() {}
};
};
int main() {
X<Y> xy;
xy.f();
} ///:~The template definition assumes that the class T that you hand it must have a nested identifier of some kind called id. Yet id could also be a static data member of T, in which case you can perform operations on id directly, but you can't “create an object” of “the type id.” In this example, the identifier id is being treated as if it were a nested type inside T. In the case of class Y, id is in fact a nested type, but (without the typename keyword) the compiler can't know that when it's compiling X.
If the compiler has the option of treating an identifier as a type or as something other than a type when it sees an identifier in a template, it will assume that the identifier refers to something other than a type. That is, it will assume that the identifier refers to an object (including variables of primitive types), an enumeration, or something similar. However, it will not—cannot—just assume that it is a type.
Because the default behavior of the compiler is to assume that a name that fits the above two points is not a type, you must use typename for nested names (except in constructor initializer lists, where it is neither needed nor allowed). In the above example, when the compiler sees typenameT::id, it knows (because of the typename keyword) that id refers to a nested type and thus it can create an object of that type.
The short version of the rule is: if a type referred to inside template code is qualified by a template type parameter, you must use the typename keyword as a prefix, unless it appears in a base class specification or initializer list in the same scope (in which case you must not).
The above explains the use of the typename keyword in the program TempTemp4.cpp. Without it, the compiler would assume that the expression Seq<T>::iterator is not a type, but we were using it to define the return type of the begin( ) and end( ) member functions.
The following example, which defines a function template that can print any Standard C++ sequence, shows a similar use of typename:
//: C05:PrintSeq.cpp {-msc}{-mwcc}
// A print function for Standard C++ sequences.
#include <iostream>
#include <list>
#include <memory>
#include <vector>
using namespace std;
template<class T, template<class U, class =
allocator<U> >
class Seq>
void printSeq(Seq<T>& seq) {
for(typename Seq<T>::iterator b = seq.begin();
b != seq.end();)
cout << *b++ << endl;
}
int main() {
// Process a vector
vector<int> v;
v.push_back(1);
v.push_back(2);
printSeq(v);
// Process a list
list<int> lst;
lst.push_back(3);
lst.push_back(4);
printSeq(lst);
} ///:~Once again, without the typename keyword the compiler will interpret iterator as a static data member of Seq<T>, which is a syntax error, since a type is required.
Typedefing a typename
It's important not to assume that the typename keyword creates a new type name. It doesn't. Its purpose is to inform the compiler that the qualified identifier is to be interpreted as a type. A line that reads:
typename Seq<T>::iterator It;causes a variable named It to be declared of type Seq<T>::iterator. If you mean to create a new type name, you should use typedef, as usual, as in:
typedef typename Seq<It>::iterator It;Using typename instead of class
Another role of the typename keyword is to provide you the option of using typename instead of class in the template argument list of a template definition:
//: C05:UsingTypename.cpp
// Using 'typename' in the template argument list.
template<typename T> class X {};
int main() {
X<int> x;
} ///:~To some, this produces clearer code.
2-3-1-5. Using the template keyword as a hint▲
Just as the typename keyword helps the compiler when a type identifier is not expected, there is also a potential difficulty with tokens that are not identifiers, such as the < and > characters. Sometimes these represent the less-than or greater-than symbols, and sometimes they delimit template parameter lists. As an example, we'll once more use the bitset class:
//: C05:DotTemplate.cpp
// Illustrate the .template construct.
#include <bitset>
#include <cstddef>
#include <iostream>
#include <string>
using namespace std;
template<class charT, size_t N>
basic_string<charT> bitsetToString(const
bitset<N>& bs) {
return bs. template to_string<charT,
char_traits<charT>,
allocator<charT>
>();
}
int main() {
bitset<10> bs;
bs.set(1);
bs.set(5);
cout << bs << endl; // 0000100010
string s = bitsetToString<char>(bs);
cout << s << endl; // 0000100010
} ///:~The bitset class supports conversion to string object via its to_string member function. To support multiple string classes, to_string is itself a template, following the pattern established by the basic_string template discussed in Chapter 3. The declaration of to_string inside of bitset looks like this:
template<class charT, class traits, class
Allocator>
basic_string<charT, traits, Allocator> to_string() const;Our bitsetToString( ) function template above requests different types of string representations of a bitset. To get a wide string, for instance, you change the call to the following:
wstring s = bitsetToString<wchar_t>(bs);Note that basic_string uses default template arguments, so we don't need to repeat the char_traits and allocator arguments in the return value. Unfortunately, bitset::to_string does not use default arguments. Using bitsetToString<char>( bs) is more convenient than typing a fully-qualified call to bs.template to_string<char, char_traits, allocator<char> >( ) every time.
The return statement in bitsetToString( ) contains the template keyword in an odd place—right after the dot operator applied to the bitset object bs. This is because when the template is parsed, the < character after the to_string token would be interpreted as a less-than operation instead of the beginning of a template argument list. The template keyword used in this context tells the compiler that what follows is the name of a template, causing the < character to be interpreted correctly. The same reasoning applies to the -> and ::operators when applied to templates. As with the typename keyword, this template disambiguation technique can only be used within template code.(52)
2-3-1-6. Member Templates▲
The bitset::to_string( ) function template is an example of a member template: a template declared within another class or class template. This allows many combinations of independent template arguments to be combined. A useful example is found in the complex class template in the Standard C++ library. The complex template has a type parameter meant to represent an underlying floating-point type to hold the real and imaginary parts of a complex number. The following code snippet from the standard library shows a member-template constructor in the complex class template:
template<typename T> class
complex {
public:
template<class X> complex(const complex<X>&);The standard complex template comes ready-made with specializations that use float, double, and long double for the parameter T. The member-template constructor above creates a new complex number that uses a different floating-point type as its base type, as seen in the code below:
complex<float> z(1, 2);
complex<double> w(z);In the declaration of w, the complex template parameter T is double and X is float. Member templates make this kind of flexible conversion easy.
Defining a template within a template is a nesting operation, so the prefixes that introduce the templates must reflect this nesting if you define the member template outside the outer class definition. For example, if you implement the complex class template, and if you define the member-template constructor outside the complex template class definition, you do it like this:
template<typename T>
template<typename X>
complex<T>::complex(const
complex<X>& c) {/* Body here… */}Another use of member function templates in the standard library is in the initialization of containers. Suppose we have a vector of ints and we want to initialize a new vector of doubles with it, like this:
int data[5] = { 1, 2, 3, 4, 5 };
vector<int> v1(data, data+5);
vector<double> v2(v1.begin(), v1.end());As long as the elements in v1 are assignment-compatible with the elements in v2 (as double and int are here), all is well. The vector class template has the following member template constructor:
template<class InputIterator>
vector(InputIterator first, InputIterator last,
const Allocator& = Allocator());This constructor is used twice in the vector declarations above. When v1 is initialized from the array of ints, the type InputIterator is int*. When v2 is initialized from v1, an instance of the member template constructor is used with InputIterator representing vector<int>::iterator.
Member templates can also be classes. (They don't need to be functions.) The following example shows a member class template inside an outer class template:
//: C05:MemberClass.cpp
// A member class template.
#include <iostream>
#include <typeinfo>
using namespace std;
template<class T> class Outer {
public:
template<class R> class Inner {
public:
void f();
};
};
template<class T> template<class R>
void Outer<T>::Inner<R>::f() {
cout << "Outer == " <<
typeid(T).name() << endl;
cout << "Inner == " <<
typeid(R).name() << endl;
cout << "Full Inner == " <<
typeid(*this).name() << endl;
}
int main() {
Outer<int>::Inner<bool> inner;
inner.f();
} ///:~The typeid operator, covered in Chapter 8, takes a single argument and returns a type_info object whose name( ) function yields a string representing the argument type. For example, typeid(int).name( ) might return the string “int.” (The actual string is platform-dependent.) The typeid operator can also take an expression and return a type_info object representing the type of that expression. For example, with int i, typeid(i).name( ) returns something like “int,” and typeid(&i).name( ) returns something like “int *.”
The output of the program above should be something like this:
Outer == int
Inner == bool
Full Inner == Outer<int>::Inner<bool>The declaration of the variable inner in the main program instantiates both Inner<bool> and Outer<int>.
Member template functions cannot be declared virtual. Current compiler technology expects to be able to determine the size of a class's virtual function table when the class is parsed. Allowing virtual member template functions would require knowing all calls to such member functions everywhere in the program ahead of time. This is not feasible, especially for multi-file projects.
2-3-2. Function template issues▲
Just as a class template describes a family of classes, a function template describes a family of functions. The syntax for creating either type of template is virtually identical, but they differ somewhat in how they are used. You must always use angle brackets when instantiating class templates and you must supply all non-default template arguments. However, with function templates you can often omit the template arguments, and default template arguments are not even allowed. Consider a typical implementation of the min( ) function template declared in the <algorithm> header, which looks something like this:
template<typename T> const T& min(const
T& a, const T& b) {
return (a < b) ? a : b;
}You could invoke this template by providing the type of the arguments in angle brackets, just like you do with class templates, as in:
int z = min<int>(i, j);This syntax tells the compiler that a specialization of the min( ) template is needed with int used in place of the parameter T, whereupon the compiler generates the corresponding code. Following the pattern of naming the classes generated from class templates, you can think of the name of the instantiated function as min<int>( ).
2-3-2-1. Type deduction of function template arguments▲
You can always use such explicit function template specification as in the example above, but it is often convenient to leave off the template arguments and let the compiler deduce them from the function arguments, like this:
int z = min(i, j);If both i and j are ints, the compiler knows that you need min<int>( ), which it then instantiates automatically. The types must be identical because the template was originally specified with only one template type argument used for both function parameters. No standard conversions are applied for function arguments whose type is specified by a template parameter. For example, if you wanted to find the minimum of an int and a double, the following attempt at a call to min( ) would fail:
int z = min(x, j); // x is a doubleSince x and j are distinct types, no single parameter matches the template parameter T in the definition of min( ), so the call does not match the template declaration. You can work around this difficulty by casting one argument to the other's type or by reverting to the fully-specified call syntax, as in:
int z = min<double>(x, j);This tells the compiler to generate the double version of min( ), after which j can be promoted to a double by normal standard conversion rules (because the function min<double>(const double&, const double&) would then exist).
You might be tempted to require two parameters for min( ), allowing the types of the arguments to be independent, like this:
template<typename T, typename
U>
const T& min(const T& a,
const U& b) {
return (a < b) ? a : b;
}This is often a good strategy, but here it is problematic because min( ) must return a value, and there is no satisfactory way to determine which type it should be (T or U?).
If the return type of a function template is an independent template parameter, you must always specify its type explicitly when you call it, since there is no argument from which to deduce it. Such is the case with the fromString template below.
//: C05:StringConv.h
// Function templates to convert to and from strings.
#ifndef STRINGCONV_H
#define STRINGCONV_H
#include <string>
#include <sstream>
template<typename T> T fromString(const
std::string& s) {
std::istringstream is(s);
T t;
is >> t;
return t;
}
template<typename T> std::string toString(const
T& t) {
std::ostringstream s;
s << t;
return s.str();
}
#endif // STRINGCONV_H ///:~These function templates provide conversions to and from std::string for any types that provide a stream inserter or extractor, respectively. Here's a test program that includes the use of the standard library complex number type:
//: C05:StringConvTest.cpp
#include <complex>
#include <iostream>
#include "StringConv.h"
using namespace std;
int main() {
int i = 1234;
cout << "i == \""
<< toString(i) << "\"" << endl;
float x = 567.89;
cout << "x == \"" <<
toString(x) << "\"" << endl;
complex<float> c(1.0, 2.0);
cout << "c == \"" <<
toString(c) << "\"" << endl;
cout << endl;
i =
fromString<int>(string("1234"));
cout << "i == "
<< i << endl;
x = fromString<float>(string("567.89"));
cout << "x == " << x <<
endl;
c = fromString<complex<float>
>(string("(1.0,2.0)"));
cout << "c == " << c <<
endl;
} ///:~The output is what you'd expect:
i == "1234"
x == "567.89"
c == "(1,2)"
i == 1234
x == 567.89
c == (1,2)Notice that in each of the instantiations of fromString( ), the template parameter is specified in the call. If you have a function template with template parameters for the parameter types as well as the return types, it is important to declare the return type parameter first, otherwise you won't be able to omit the type parameters for the function parameters. As an illustration, consider the following well-known function template:(53)
//: C05:ImplicitCast.cpp
template<typename R, typename
P>
R implicit_cast(const P& p) {
return p;
}
int main() {
int i = 1;
float x = implicit_cast<float>(i);
int j = implicit_cast<int>(x);
//! char* p = implicit_cast<char*>(i);
} ///:~If you interchange R and P in the template parameter list near the top of the file, it will be impossible to compile this program because the return type will remain unspecified (the first template parameter would be the function's parameter type). The last line (which is commented out) is illegal because there is no standard conversion from int to char*. implicit_cast is for revealing conversions in your code that are allowed naturally.
With a little care you can even deduce array dimensions. This example has an array-initialization function template (init2) that performs such a deduction:
//: C05:ArraySize.cpp
#include <cstddef>
using std::size_t;
template<size_t R, size_t C, typename T>
void init1(T a[R][C]) {
for(size_t i = 0; i < R; ++i)
for(size_t j = 0; j < C; ++j)
a[i][j] = T();
}
template<size_t R, size_t C, class T>
void init2(T (&a)[R][C]) { // Reference parameter
for(size_t i = 0; i < R; ++i)
for(size_t j = 0; j < C; ++j)
a[i][j] = T();
}
int main() {
int a[10][20];
init1<10,20>(a); // Must specify
init2(a); // Sizes deduced
} ///:~Array dimensions are not passed as part of a function parameter's type unless that parameter is passed by pointer or reference. The function template init2 declares a to be a reference to a two-dimensional array, so its dimensions R and C are deduced by the template facility, making init2 a handy way to initialize a two-dimensional array of any size. The template init1 does not pass the array by reference, so the sizes must be explicitly specified, although the type parameter can still be deduced.
2-3-2-2. Function template overloading▲
As with ordinary functions, you can overload function templates that have the same name. When the compiler processes a function call in a program, it has to decide which template or ordinary function is the “best” fit for the call. Along with the min( ) function template introduced earlier, let's add some ordinary functions to the mix:
//: C05:MinTest.cpp
#include <cstring>
#include <iostream>
using std::strcmp;
using std::cout;
using std::endl;
template<typename T> const T& min(const
T& a, const T& b) {
return (a < b) ? a : b;
}
const char* min(const char* a, const char* b) {
return (strcmp(a, b) < 0) ? a : b;
}
double min(double x, double y) {
return (x < y) ? x : y;
}
int main() {
const char *s2 = "say \"Ni-!\"",
*s1 = "knights who";
cout << min(1, 2) << endl; // 1: 1
(template)
cout << min(1.0, 2.0) << endl; // 2: 1
(double)
cout << min(1, 2.0) << endl; // 3: 1
(double)
cout << min(s1, s2) << endl; // 4:
knights who (const
//
char*)
cout << min<>(s1, s2) << endl; //
5: say "Ni-!"
// (template)
} ///:~In addition to the function template, this program defines two non-template functions: a C-style string version of min( ) and a double version. If the template doesn't exist, the call in line 1 above invokes the double version of min( ) because of the standard conversion from int to double. The template can generate an int version which is considered a better match, so that's what happens. The call in line 2 is an exact match for the double version, and the call in line 3 also invokes the same function, implicitly converting 1 to 1.0. In line 4 the const char* version of min( ) is called directly. In line 5 we force the compiler to use the template facility by appending empty angle brackets to the function name, whereupon it generates a const char* version from the template and uses it (which is verified by the wrong answer—it's just comparing addresses!(54)). If you're wondering why we have using declarations in lieu of the using namespace std directive, it's because some compilers include headers behind the scenes that bring in std::min( ), which would conflict with our declarations of the name min( ).
As stated above, you can overload templates of the same name, as long as they can be distinguished by the compiler. You could, for example, declare a min( ) function template that processes three arguments:
template<typename T>
const T& min(const T& a, const T& b, const T& c);Versions of this template will be generated only for calls to min( ) that have three arguments of the same type.
2-3-2-3. Taking the address of a generated function template▲
In some situations you need to take the address of a function. For example, you may have a function that takes an argument of a pointer to another function. It's possible that this other function might be generated from a template function, so you need some way to take that kind of address:(55)
//: C05:TemplateFunctionAddress.cpp {-mwcc}
// Taking the address of a function generated
// from a template.
template<typename T> void f(T*) {}
void h(void (*pf)(int*)) {}
template<typename T> void g(void (*pf)(T*)) {}
int main() {
h(&f<int>); // Full type specification
h(&f); // Type deduction
g<int>(&f<int>); // Full type
specification
g(&f<int>); // Type deduction
g<int>(&f); // Partial (but sufficient)
specification
} ///:~This example demonstrates a number of issues. First, even though you're using templates, the signatures must match. The function h( ) takes a pointer to a function that takes an int* and returns void, and that's what the template f( ) produces. Second, the function that wants the function pointer as an argument can itself be a template, as in the case of the template g( ).
In main( ) you can see that type deduction works here, too. The first call to h( ) explicitly gives the template argument for f( ), but since h( ) says that it will only take the address of a function that takes an int*, that part can be deduced by the compiler. With g( ) the situation is even more interesting because two templates are involved. The compiler cannot deduce the type with nothing to go on, but if either f( ) or g( ) is given int, the rest can be deduced.
An obscure issue arises when trying to pass the functions tolower or toupper, declared in <cctype>, as parameters. It is possible to use these, for example, with the transform algorithm (which is covered in detail in the next chapter) to convert a string to lower or upper case. You must be careful because there are multiple declarations for these functions. A naive approach would be something like this:
// The variable s is a std::string
transform(s.begin(), s.end(), s.begin(), tolower);The transform algorithm applies its fourth parameter (tolower( ) in this case) to each character in the string s and places the result in s itself, thus overwriting each character in s with its lower-case equivalent. As it is written, this statement may or may not work! It fails in the following context:
//: C05:FailedTransform.cpp {-xo}
#include <algorithm>
#include <cctype>
#include <iostream>
#include <string>
using namespace std;
int main() {
string s("LOWER");
transform(s.begin(), s.end(), s.begin(), tolower);
cout << s << endl;
} ///:~Even if your compiler lets you get away with this, it is illegal. The reason is that the <iostream> header also makes available a two-argument version of tolower( ) and toupper( ):
template<class charT> charT toupper(charT c,
const locale&
loc);
template<class charT> charT tolower(charT c,
const locale& loc);These function templates take a second argument of type locale. The compiler has no way of knowing whether it should use the one-argument version of tolower( ) defined in <cctype> or the one mentioned above. You can solve this problem (almost!) with a cast in the call to transform, as follows:
transform(s.begin(),s.end(),s.begin()
static_cast<int (*)(int)>(tolower));(Recall that tolower( ) and toupper( ) work with int instead of char.) The cast above makes clear that the single-argument version of tolower( ) is desired. This works with some compilers, but it is not required to. The reason, albeit obscure, is that a library implementation is allowed to give “C linkage” (meaning that the function name does not contain all the auxiliary information(56) that normal C++ functions do) to functions inherited from the C language. If this is the case, the cast fails because transform is a C++ function template and expects its fourth argument to have C++ linkage—and a cast is not allowed to change the linkage. What a predicament!
The solution is to place tolower( ) calls in an unambiguous context. For example, you could write a function named strTolower( ) and place it in its own file without including <iostream>, like this:
//: C05:StrTolower.cpp {O} {-mwcc}
#include <algorithm>
#include <cctype>
#include <string>
using namespace std;
string strTolower(string s) {
transform(s.begin(), s.end(), s.begin(), tolower);
return s;
} ///:~The header <iostream> is not involved here, and the compilers we use do not introduce the two-argument version of tolower( ) in this context,(57) so there's no problem. You can then use this function normally:
//: C05:Tolower.cpp {-mwcc}
//{L} StrTolower
#include <algorithm>
#include <cctype>
#include <iostream>
#include <string>
using namespace std;
string strTolower(string);
int main() {
string s("LOWER");
cout << strTolower(s) << endl;
} ///:~Another solution is to write a wrapper function template that calls the correct version of tolower( ) explicitly:
//: C05:ToLower2.cpp {-mwcc}
#include <algorithm>
#include <cctype>
#include <iostream>
#include <string>
using namespace std;
template<class charT> charT strTolower(charT c) {
return tolower(c); // One-arg version called
}
int main() {
string s("LOWER");
transform(s.begin(),s.end(),s.begin(),&strTolower<char>);
cout << s << endl;
} ///:~This version has the advantage that it can process both wide and narrow strings since the underlying character type is a template parameter. The C++ Standards Committee is working on modifying the language so that the first example (without the cast) will work, and some day these workarounds can be ignored.(58)
2-3-2-4. Applying a function to an STL sequence▲
Suppose you want to take an STL sequence container (which you'll learn more about in subsequent chapters; for now we can just use the familiar vector) and apply a member function to all the objects it contains. Because a vector can contain any type of object, you need a function that works with any type of vector:
//: C05:ApplySequence.h
// Apply a function to an STL sequence container.
// const, 0 arguments, any type of return value:
template<class Seq, class T, class R>
void apply(Seq& sq, R (T::*f)() const) {
typename Seq::iterator it = sq.begin();
while(it != sq.end())
((*it++)->*f)();
}
// const, 1 argument, any type of return value:
template<class Seq, class T, class R, class A>
void apply(Seq& sq, R(T::*f)(A) const, A a) {
typename Seq::iterator it = sq.begin();
while(it != sq.end())
((*it++)->*f)(a);
}
// const, 2 arguments, any type of return value:
template<class Seq, class T, class R,
class A1, class A2>
void apply(Seq& sq, R(T::*f)(A1, A2) const,
A1 a1, A2 a2) {
typename Seq::iterator it = sq.begin();
while(it != sq.end())
((*it++)->*f)(a1, a2);
}
// Non-const, 0 arguments, any type of return value:
template<class Seq, class T, class R>
void apply(Seq& sq, R (T::*f)()) {
typename Seq::iterator it = sq.begin();
while(it != sq.end())
((*it++)->*f)();
}
// Non-const, 1 argument, any type of return value:
template<class Seq, class T, class R, class A>
void apply(Seq& sq, R(T::*f)(A), A a) {
typename Seq::iterator it = sq.begin();
while(it != sq.end())
((*it++)->*f)(a);
}
// Non-const, 2 arguments, any type of return value:
template<class Seq, class T, class R,
class A1, class A2>
void apply(Seq& sq, R(T::*f)(A1, A2),
A1 a1, A2 a2) {
typename Seq::iterator it = sq.begin();
while(it != sq.end())
((*it++)->*f)(a1, a2);
}
// Etc., to handle maximum
likely arguments ///:~The apply( ) function template above takes a reference to the container class and a pointer-to-member for a member function of the objects contained in the class. It uses an iterator to move through the sequence and apply the function to every object. We have overloaded on the const-ness of the function so you can use it with both const and non-const functions.
Notice that there are no STL header files (or any header files, for that matter) included in applySequence.h, so it is not limited to use with an STL container. However, it does make assumptions (primarily, the name and behavior of the iterator) that apply to STL sequences, and it also assumes that the elements of the container be of pointer type.
You can see there is more than one version of apply( ), further illustrating overloading of function templates. Although these templates allow any type of return value (which is ignored, but the type information is required to match the pointer-to-member), each version takes a different number of arguments, and because it's a template, those arguments can be of any type. The only limitation here is that there's no “super template” to create templates for you; you must decide how many arguments will ever be required and make the appropriate definitions.
To test the various overloaded versions of apply( ), the class Gromit(59) is created containing functions with different numbers of arguments, and both const and non-const member functions:
//: C05:Gromit.h
// The techno-dog. Has member functions
// with various numbers of arguments.
#include <iostream>
class Gromit {
int arf;
int totalBarks;
public:
Gromit(int arf = 1) : arf(arf + 1), totalBarks(0) {}
void speak(int) {
for(int i = 0; i < arf; i++) {
std::cout << "arf! ";
++totalBarks;
}
std::cout << std::endl;
}
char eat(float) const {
std::cout << "chomp!" <<
std::endl;
return 'z';
}
int sleep(char, double) const {
std::cout << "zzz..." <<
std::endl;
return 0;
}
void sit() const {
std::cout << "Sitting..." <<
std::endl;
}
}; ///:~Now you can use the apply( ) template functions to apply the Gromit member functions to a vector<Gromit*>, like this:
//: C05:ApplyGromit.cpp
// Test ApplySequence.h.
#include <cstddef>
#include <iostream>
#include <vector>
#include "ApplySequence.h"
#include "Gromit.h"
#include "../purge.h"
using namespace std;
int main() {
vector<Gromit*> dogs;
for(size_t i = 0; i < 5; i++)
dogs.push_back(new Gromit(i));
apply(dogs, &Gromit::speak, 1);
apply(dogs, &Gromit::eat, 2.0f);
apply(dogs, &Gromit::sleep, 'z', 3.0);
apply(dogs, &Gromit::sit);
purge(dogs);
} ///:~The purge( ) function is a small utility that calls delete on every element of sequence. You'll find it defined in Chapter 7, and used various places in this book.
Although the definition of apply( ) is somewhat complex and not something you'd ever expect a novice to understand, its use is remarkably clean and simple, and a novice could use it knowing only what it is intended to accomplish, not how. This is the type of division you should strive for in all your program components. The tough details are all isolated on the designer's side of the wall. Users are concerned only with accomplishing their goals and don't see, know about, or depend on details of the underlying implementation. We'll explore even more flexible ways to apply functions to sequences in the next chapter.
2-3-2-5. Partial ordering of function templates▲
We mentioned earlier that an ordinary function overload of min( ) is preferable to using the template. If a function already exists to match a function call, why generate another? In the absence of ordinary functions, however, it is possible that overloaded function templates can lead to ambiguities. To minimize the chances of this, an ordering is defined for function templates, which chooses the most specialized template, if such exists. A function template is considered more specialized than another if every possible list of arguments that matches it also matches the other, but not the other way around. Consider the following function template declarations, taken from an example in the C++ Standard document:
template<class T> void f(T);
template<class T> void f(T*);
template<class T> void f(const T*);The first template can be matched with any type. The second template is more specialized than the first because only pointer types match it. In other words, you can look upon the set of possible calls that match the second template as a subset of the first. A similar relationship exists between the second and third template declarations above: the third can only be called for pointers to const, but the second accommodates any pointer type. The following program illustrates these rules:
//: C05:PartialOrder.cpp
// Reveals ordering of function templates.
#include <iostream>
using namespace std;
template<class T> void f(T) {
cout << "T" << endl;
}
template<class T> void f(T*) {
cout << "T*" << endl;
}
template<class T> void f(const T*) {
cout << "const T*" << endl;
}
int main() {
f(0); // T
int i = 0;
f(&i); // T*
const int j = 0;
f(&j); // const T*
} ///:~The call f(&i) certainly matches the first template, but since the second is more specialized, it is called. The third can't be called here since the pointer is not a pointer to const. The call f(&j) matches all three templates (for example, T would be const int in the second template), but again, the third template is more specialized, so it is used instead.
If there is no “most specialized” template among a set of overloaded function templates, an ambiguity remains, and the compiler will report an error. That is why this feature is called a “partial ordering”—it may not be able to resolve all possibilities. Similar rules exist for class templates (see the section “Partial specialization” below).
2-3-3. Template specialization▲
The term specialization has a specific, template-related meaning in C++. A template definition is, by its very nature, a generalization, because it describes a family of functions or classes in general terms. When template arguments are supplied, the result is a specialization of the template because it determines a unique instance out of the many possible instances of the family of functions or classes. The min( ) function template seen at the beginning of this chapter is a generalization of a minimum-finding function because the type of its parameters is not specified. When you supply the type for the template parameter, whether explicitly or implicitly via argument deduction, the resultant code generated by the compiler (for example, min<int>( )) is a specialization of the template. The code generated is also considered an instantiation of the template, as are all code bodies generated by the template facility.
2-3-3-1. Explicit specialization▲
You can also provide the code yourself for a given template specialization, should the need arise. Providing your own template specializations is often needed with class templates, but we will begin with the min( ) function template to introduce the syntax.
Recall that in MinTest.cpp earlier in this chapter we introduced the following ordinary function:
const char* min(const char* a, const char* b) {
return (strcmp(a, b) < 0) ? a : b;
}This was so that a call to min( ) would compare strings and not addresses. Although it would provide no advantage here, we could instead define a const char* specialization for min( ), as in the following program:
//: C05:MinTest2.cpp
#include <cstring>
#include <iostream>
using std::strcmp;
using std::cout;
using std::endl;
template<class T> const T& min(const T&
a, const T& b) {
return (a < b) ? a : b;
}
// An explicit specialization of the min template
template<>
const char* const& min<const char*>(const
char* const& a,
const char*
const& b) {
return (strcmp(a, b) < 0) ? a : b;
}
int main() {
const char *s2 = "say \"Ni-!\"",
*s1 = "knights who";
cout << min(s1, s2) << endl;
cout << min<>(s1, s2) << endl;
} ///:~The “template<>” prefix tells the compiler that what follows is a specialization of a template. The type for the specialization must appear in angle brackets immediately following the function name, as it normally would in an explicitly specified call. Note that we carefully substitute const char* for T in the explicit specialization. Whenever the original template specifies const T, that const modifies the whole type T. It is the pointer to a const char* that is const. So we must write const char* const in place of const T in the specialization. When the compiler sees a call to min( ) with const char* arguments in the program, it will instantiate our const char* version of min( ) so it can be called. The two calls to min( ) in this program call the same specialization of min( ).
Explicit specializations tend to be more useful for class templates than for function templates. When you provide a full specialization for a class template, though, you may need to implement all the member functions. This is because you are providing a separate class, and client code may expect the complete interface to be implemented.
The standard library has an explicit specialization for vector when it holds objects of type bool. The purpose for vector<bool> is to allow library implementations to save space by packing bits into integers.(60)
As you saw earlier in this chapter, the declaration for the primary vector class template is:
template<class T, class Allocator =
allocator<T> >
class vector {...};To specialize for objects of type bool, you could declare an explicit specialization as follows:
template<> class
vector<bool, allocator<bool> > {...};Again, this is quickly recognized as a full, explicit specialization because of the template<> prefix and because all the primary template's parameters are satisfied by the argument list appended to the class name.
It turns out that vector<bool> is a little more flexible than we have described, as seen in the next section.
2-3-3-2. Partial Specialization▲
Class templates can also be partially specialized, meaning that at least one of the template parameters is left “open” in some way in the specialization. vector<bool> specifies the object type (bool), but leaves the allocator type unspecified. Here is the actual declaration of vector<bool>:
template<class Allocator> class vector<bool,
Allocator>;You can recognize a partial specialization because non-empty parameter lists appear in angle brackets both after the template keyword (the unspecified parameters) and after the class (the specified arguments). Because of the way vector<bool> is defined, a user can provide a custom allocator type, even though the contained type of bool is fixed. In other words, specialization, and partial specialization in particular, constitute a sort of “overloading” for class templates.
Partial ordering of class templates
The rules that determine which template is selected for instantiation are similar to the partial ordering for function templates—the “most specialized” template is selected. The string in each f( ) member function in the illustration below explains the role of each template definition:
//: C05:PartialOrder2.cpp
// Reveals partial ordering of class templates.
#include <iostream>
using namespace std;
template<class T, class U> class C {
public:
void f() { cout << "Primary Template\n";
}
};
template<class U> class C<int, U> {
public:
void f() { cout << "T == int\n"; }
};
template<class T> class C<T, double> {
public:
void f() { cout << "U == double\n”; }
};
template<class T, class U> class C<T*, U> {
public:
void f() { cout << "T* used\n”; }
};
template<class T, class U> class C<T, U*> {
public:
void f() { cout << "U* used\n”; }
};
template<class T, class U> class C<T*, U*>
{
public:
void f() { cout << "T* and U* used\n”; }
};
template<class T> class C<T, T> {
public:
void f() { cout << "T == U\n”; }
};
int main() {
C<float, int>().f(); // 1: Primary template
C<int, float>().f(); // 2: T == int
C<float, double>().f(); // 3: U == double
C<float, float>().f(); // 4: T == U
C<float*, float>().f(); // 5: T* used [T is
float]
C<float, float*>().f(); // 6: U* used [U is
float]
C<float*, int*>().f(); // 7: T* and U* used
[float,int]
// The following are ambiguous:
// 8: C<int, int>().f();
// 9: C<double, double>().f();
// 10: C<float*, float*>().f();
// 11: C<int, int*>().f();
// 12: C<int*, int*>().f();
} ///:~As you can see, you can partially specify template parameters according to whether they are pointer types, or whether they are equal. When the T* specialization is used, such as is the case in line 5, T itself is not the top-level pointer type that was passed—it is the type that the pointer refers to (float, in this case). The T* specification is a pattern to allow matching against pointer types. If you use int** as the first template argument, T becomes int*. Line 8 is ambiguous because having the first parameter as an int versus having the two parameters equal are independent issues—one is not more specialized than the other. Similar logic applies to lines 9 through 12.
2-3-3-3. A practical example▲
You can easily derive from a class template, and you can create a new template that instantiates and inherits from an existing template. If the vector template does most everything you want, for example, but in a certain application you'd also like a version that can sort itself, you can easily reuse the vector code. The following example derives from vector<T> and adds sorting. Note that deriving from vector, which doesn't have a virtual destructor, would be dangerous if we needed to perform cleanup in our destructor.
//: C05:Sortable.h
// Template specialization.
#ifndef SORTABLE_H
#define SORTABLE_H
#include <cstring>
#include <cstddef>
#include <string>
#include <vector>
using std::size_t;
template<class T>
class Sortable : public std::vector<T> {
public:
void sort();
};
template<class T>
void Sortable<T>::sort() { // A simple sort
for(size_t i = this->size(); i > 0; --i)
for(size_t j = 1; j < i; ++j)
if(this->at(j-1) > this->at(j)) {
T t = this->at(j-1);
this->at(j-1) = this->at(j);
this->at(j) = t;
}
}
// Partial specialization for
pointers:
template<class T>
class Sortable<T*> :
public std::vector<T*> {
public:
void sort();
};
template<class T>
void Sortable<T*>::sort() {
for(size_t i = this->size(); i > 0; --i)
for(size_t j = 1; j < i; ++j)
if(*this->at(j-1) > *this->at(j)) {
T* t = this->at(j-1);
this->at(j-1) = this->at(j);
this->at(j) = t;
}
}
// Full specialization for char*
// (Made inline here for
convenience -- normally you would
// place the function body in a separate
file and only
// leave the declaration here).
template<> inline void Sortable<char*>::sort()
{
for(size_t i = this->size(); i > 0; --i)
for(size_t j = 1; j < i; ++j)
if(std::strcmp(this->at(j-1), this->at(j))
> 0) {
char* t = this->at(j-1);
this->at(j-1) = this->at(j);
this->at(j) = t;
}
}
#endif // SORTABLE_H ///:~The Sortable template imposes a restriction on all but one of the classes for which it is instantiated: they must contain a > operator. It works correctly only with non-pointer objects (including objects of built-in types). The full specialization compares the elements using strcmp( ) to sort vectors of char* according to the null-terminated strings to which they refer. The use of “this->” above is mandatory(61) and is explained in the section entitled “Name lookup issues” later in this chapter.(62)
Here's a driver for Sortable.h that uses the randomizer introduced earlier in the chapter:
//: C05:Sortable.cpp
//{-bor} (Because of bitset in Urand.h)
// Testing template specialization.
#include <cstddef>
#include <iostream>
#include "Sortable.h"
#include "Urand.h"
using namespace std;
#define asz(a) (sizeof a / sizeof a[0])
char* words[] = { "is", "running",
"big", "dog", "a", };
char* words2[] = { "this", "that",
"theother", };
int main() {
Sortable<int> is;
Urand<47> rnd;
for(size_t i = 0; i < 15; ++i)
is.push_back(rnd());
for(size_t i = 0; i < is.size(); ++i)
cout << is[i] << ' ';
cout << endl;
is.sort();
for(size_t i = 0; i < is.size(); ++i)
cout << is[i] << ' ';
cout << endl;
// Uses the template partial specialization:
Sortable<string*> ss;
for(size_t i = 0; i < asz(words); ++i)
ss.push_back(new string(words[i]));
for(size_t i = 0; i < ss.size(); ++i)
cout << *ss[i] << ' ';
cout << endl;
ss.sort();
for(size_t i = 0; i < ss.size(); ++i) {
cout << *ss[i] << ' ';
delete ss[i];
}
cout << endl;
// Uses the full char* specialization:
Sortable<char*> scp;
for(size_t i = 0; i < asz(words2); ++i)
scp.push_back(words2[i]);
for(size_t i = 0; i < scp.size(); ++i)
cout << scp[i] << ' ';
cout << endl;
scp.sort();
for(size_t i = 0; i < scp.size(); ++i)
cout << scp[i] << ' ';
cout << endl;
} ///:~Each of the template instantiations above uses a different version of the template. Sortable<int> uses the primary template. Sortable<string*> uses the partial specialization for pointers. Last, Sortable<char*> uses the full specialization for char*. Without this full specialization, you could be fooled into thinking that things were working correctly because the words array would still sort out to “a big dog is running” since the partial specialization would end up comparing the first character of each array. However, words2 would not sort correctly.
2-3-3-4. Preventing template code bloat▲
Whenever a class template is instantiated, the code from the class definition for the particular specialization is generated, along with all the member functions that are called in the program. Only the member functions that are called are generated. This is good, as you can see in the following program:
//: C05:DelayedInstantiation.cpp
// Member functions of class templates are not
// instantiated until they're needed.
class X {
public:
void f() {}
};
class Y {
public:
void g() {}
};
template<typename T> class Z {
T t;
public:
void a() { t.f(); }
void b() { t.g(); }
};
int main() {
Z<X> zx;
zx.a(); // Doesn't create Z<X>::b()
Z<Y> zy;
zy.b(); // Doesn't create Z<Y>::a()
} ///:~Here, even though the template Z purports to use both f( ) and g( ) member functions of T, the fact that the program compiles shows you that it only generates Z<X>::a( ) when it is explicitly called for zx. (If Z<X>::b( ) were also generated at the same time, a compile-time error message would be generated because it would attempt to call X::g( ), which doesn't exist.) Similarly, the call to zy.b( ) doesn't generate Z<Y>::a( ). As a result, the Z template can be used with X and Y, whereas if all the member functions were generated when the class was first instantiated the use of many templates would become significantly limited.
Suppose you have a templatized Stack container and you use specializations for int, int*, and char*. Three versions of Stack code will be generated and linked as part of your program. One of the reasons for using a template in the first place is so you don't need to replicate code by hand; but code still gets replicated—it's just the compiler that does it instead of you. You can factor the bulk of the implementation for storing pointer types into a single class by using a combination of full and partial specialization. The key is to fully specialize for void* and then derive all other pointer types from the void* implementation so the common code can be shared. The program below illustrates this technique:
//: C05:Nobloat.h
// Shares code for storing pointers in a Stack.
#ifndef NOBLOAT_H
#define NOBLOAT_H
#include <cassert>
#include <cstddef>
#include <cstring>
// The primary template
template<class T> class Stack {
T* data;
std::size_t count;
std::size_t capacity;
enum { INIT = 5 };
public:
Stack() {
count = 0;
capacity = INIT;
data = new T[INIT];
}
void push(const T& t) {
if(count == capacity) {
// Grow array store
std::size_t newCapacity = 2 * capacity;
T* newData = new T[newCapacity];
for(size_t i = 0; i < count; ++i)
newData[i] = data[i];
delete [] data;
data = newData;
capacity = newCapacity;
}
assert(count < capacity);
data[count++] = t;
}
void pop() {
assert(count > 0);
--count;
}
T top() const {
assert(count > 0);
return data[count-1];
}
std::size_t size() const { return count; }
};
// Full specialization for void*
template<> class Stack<void *> {
void** data;
std::size_t count;
std::size_t capacity;
enum { INIT = 5 };
public:
Stack() {
count = 0;
capacity = INIT;
data = new void*[INIT];
}
void push(void* const & t) {
if(count == capacity) {
std::size_t newCapacity = 2*capacity;
void** newData = new void*[newCapacity];
std::memcpy(newData, data, count*sizeof(void*));
delete [] data;
data = newData;
capacity = newCapacity;
}
assert(count < capacity);
data[count++] = t;
}
void pop() {
assert(count > 0);
--count;
}
void* top() const {
assert(count > 0);
return data[count-1];
}
std::size_t size() const { return count; }
};
// Partial specialization for
other pointer types
template<class T> class
Stack<T*> : private Stack<void *> {
typedef Stack<void *>
Base;
public:
void push(T* const & t) { Base::push(t); }
void pop() {Base::pop();}
T* top() const { return
static_cast<T*>(Base::top()); }
std::size_t size() { return Base::size(); }
};
#endif // NOBLOAT_H ///:~This simple stack expands as it fills its capacity. The void* specialization stands out as a full specialization by virtue of the template<> prefix (that is, the template parameter list is empty). As mentioned earlier, it is necessary to implement all member functions in a class template specialization. The savings occurs with all other pointer types. The partial specialization for other pointer types derives from Stack<void*> privately, since we are merely using Stack<void*> for implementation purposes, and do not wish to expose any of its interface directly to the user. The member functions for each pointer instantiation are small forwarding functions to the corresponding functions in Stack<void*>. Hence, whenever a pointer type other than void* is instantiated, it is a fraction of the size it would have been had the primary template alone been used.(63) Here is a driver program:
//: C05:NobloatTest.cpp
#include <iostream>
#include <string>
#include "Nobloat.h"
using namespace std;
template<class StackType>
void emptyTheStack(StackType& stk) {
while(stk.size() > 0) {
cout << stk.top() << endl;
stk.pop();
}
}
// An overload for emptyTheStack (not a
specialization!)
template<class T>
void emptyTheStack(Stack<T*>& stk) {
while(stk.size() > 0) {
cout << *stk.top() << endl;
stk.pop();
}
}
int main() {
Stack<int> s1;
s1.push(1);
s1.push(2);
emptyTheStack(s1);
Stack<int *> s2;
int i = 3;
int j = 4;
s2.push(&i);
s2.push(&j);
emptyTheStack(s2);
} ///:~For convenience we include two emptyStack function templates. Since function templates don't support partial specialization, we provide overloaded templates. The second version of emptyStack is more specialized than the first, so it is chosen whenever pointer types are used. Three class templates are instantiated in this program: Stack<int>, Stack<void*>, and Stack<int*>. Stack<void*> is implicitly instantiated because Stack<int*> derives from it. A program using instantiations for many pointer types can produce substantial savings in code size over just using a single Stack template.
2-3-4. Name lookup issues▲
When the compiler encounters an identifier it must determine the type and scope (and in the case of variables, the lifetime) of the entity the identifier represents. Templates add complexity to the situation. Because the compiler doesn't know everything about a template when it first sees the definition, it can't tell whether the template is being used properly until it sees the template instantiation. This predicament leads to a two-phase process for template compilation.
2-3-4-1. Names in templates▲
In the first phase, the compiler parses the template definition looking for obvious syntax errors and resolving all the names it can. It can resolve names that do not depend on template parameters using normal name lookup, and if necessary through argument-dependent lookup (discussed below). The names it can't resolve are the so-called dependent names, which depend on template parameters in some way. These can't be resolved until the template is instantiated with its actual arguments. So instantiation is the second phase of template compilation. Here, the compiler determines whether to use an explicit specialization of the template instead of the primary template.
Before you see an example, you must understand two more terms. A qualified name is a name with a class-name prefix, a name with an object name and a dot operator, or a name with a pointer to an object and an arrow operator. Examples of qualified names are:
MyClass::f();
x.f();
p->f();We use qualified names many times in this book, and most recently in connection with the typename keyword. These are called qualified names because the target names (like f above) are explicitly associated with a class or namespace, which tells the compiler where to look for the declarations of those names.
The other term is argument-dependent lookup(64) (ADL), a mechanism originally designed to simplify non-member function calls (including operators) declared in namespaces. Consider the following:
#include <iostream>
#include <string>
// ...
std::string s("hello");
std::cout << s << std::endl;Note that, following the typical practice in header files, there is no using namespace std directive. Without such a directive, you must use the “std::”qualifier on the items that are in the std namespace. We have, however, not qualified everything from std that we are using. Can you see what is unqualified?
We have not specified which operator functions to use. We want the following to happen, but we don't want to have to type it!
std::operator<<(std::operator<<(std::cout,s),std::endl);To make the original output statement work as desired, ADL specifies that when an unqualified function call appears and its declaration is not in (normal) scope, the namespaces of each of its arguments are searched for a matching function declaration. In the original statement, the first function call is:
operator<<(std::cout, s);Since there is no such function in scope in our original excerpt, the compiler notes that this function's first argument (std::cout) is in the namespace std; so it adds that namespace to the list of scopes to search for a unique function that best matches the signature operator<<(std::ostream&, std::string). It finds this function declared in the std namespace via the <string> header.
Namespaces would be very inconvenient without ADL. Note that ADL generally brings in all declarations of the name in question from all eligible namespaces—if there is no single best match, an ambiguity will result.
To turn off ADL, you can enclose the function name in parentheses:
(f)(x, y); // ADL suppressedNow consider the following program:(65)
//: C05:Lookup.cpp
// Only produces correct behavior with EDG,
// and Metrowerks using a special option.
#include <iostream>
using std::cout;
using std::endl;
void f(double) { cout << "f(double)"
<< endl; }
template<class T> class X {
public:
void g() { f(1); }
};
void f(int) { cout << "f(int)" <<
endl; }
int main() {
X<int>().g();
} ///:~The only compiler we have that produces correct behavior without modification is the Edison Design Group front end,(66) although some compilers, such as Metrowerks, have an option to enable the correct lookup behavior. The output should be:
f(double)because f is a non-dependent name that can be resolved early by looking in the context where the template is defined, when only f(double) is in scope. Unfortunately, there is a lot of existing code in the industry that depends on the non-standard behavior of binding the call to f(1) inside g( ) to the latter f(int), so compiler writers have been reluctant to make the change.
Here is a more detailed example:(67)
//: C05:Lookup2.cpp {-bor}{-g++}{-dmc}
// Microsoft: use option -Za (ANSI mode)
#include <algorithm>
#include <iostream>
#include <typeinfo>
using std::cout;
using std::endl;
void g() { cout << "global g()” <<
endl; }
template<class T> class Y {
public:
void g() {
cout << "Y<" <<
typeid(T).name() << ">::g()” << endl;
}
void h() {
cout << "Y<" <<
typeid(T).name() << ">::h()” << endl;
}
typedef int E;
};
typedef double E;
template<class T> void swap(T& t1, T& t2)
{
cout << "global swap” << endl;
T temp = t1;
t1 = t2;
t2 = temp;
}
template<class T> class X : public Y<T> {
public:
E f() {
g();
this->h();
T t1 = T(), t2 = T(1);
cout << t1 << endl;
swap(t1, t2);
std::swap(t1, t2);
cout << typeid(E).name() << endl;
return E(t2);
}
};
int main() {
X<int> x;
cout << x.f() << endl;
} ///:~The output from this program should be:
global g()
Y<int>::h()
0
global swap
double
1Looking at the declarations inside of X::f( ):
- E, the return type of X::f( ), is not a dependent name, so it is looked up when the template is parsed, and the typedef naming E as a double is found. This may seem strange, since with non-template classes the declaration of E in the base class would be found first, but those are the rules. (The base class, Y, is a dependent base class, so it can't be searched at template definition time).
- The call to g( ) is also non-dependent, since there is no mention of T. If g had parameters that were of class type of defined in another namespace, ADL would take over, since there is no g with parameters in scope. As it is, this call matches the global declaration of g( ).
- The call this->h( ) is a qualified name, and the object that qualifies it (this) refers to the current object, which is of type X, which in turn depends on the name Y<T> by inheritance. There is no function h( ) inside of X, so the lookup will search the scope of X's base class, Y<T>. Since this is a dependent name, it is looked up at instantiation time, when Y<T> are reliably known (including any potential specializations that might have been written after the definition of X), so it calls Y<int>::h( ).
- The declarations of t1 and t2 are dependent.
- The call to operator<<(cout, t1) is dependent, since t1 is of type T. This is looked up later when T is int, and the inserter for int is found in std.
- The unqualified call to swap( ) is dependent because its arguments are of type T. This ultimately causes a global swap(int&, int&) to be instantiated.
- The qualified call to std::swap( ) is not dependent, because std is a fixed namespace. The compiler knows to look in std for the proper declaration. (The qualifier on the left of the “::” must mention a template parameter for a qualified name to be considered dependent.) The std::swap( ) function template later generates std::swap(int&, int&), at instantiation time. No more dependent names remain in X<T>::f( ).
To clarify and summarize: name lookup is done at the point of instantiation if the name is dependent, except that for unqualified dependent names the normal name lookup is also attempted early, at the point of definition. All non-dependent names in templates are looked up early, at the time the template definition is parsed. (If necessary, another lookup occurs at instantiation time, when the type of the actual argument is known.)
If you have studied this example to the point that you understand it, prepare yourself for yet another surprise in the following section on friend declarations.
2-3-4-2. Templates and friends▲
A friend function declaration inside a class allows a non-member function to access non-public members of that class. If the friend function name is qualified, it will be found in the namespace or class that qualifies it. If it is unqualified, however, the compiler must make an assumption about where the definition of the friend function will be, since all identifiers must have a unique scope. The expectation is that the function will be defined in the nearest enclosing namespace (non-class) scope that contains the class granting friendship. Often this is just the global scope. The following non-template example clarifies this issue:
//: C05:FriendScope.cpp
#include <iostream>
using namespace std;
class Friendly {
int i;
public:
Friendly(int theInt) { i = theInt; }
friend void f(const Friendly&); // Needs global
def.
void g() { f(*this); }
};
void h() {
f(Friendly(1)); // Uses ADL
}
void f(const Friendly& fo) { // Definition of
friend
cout << fo.i << endl;
}
int main() {
h(); // Prints 1
Friendly(2).g(); // Prints 2
} ///:~The declaration of f( ) inside the Friendly class is unqualified, so the compiler will expect to be able to eventually link that declaration to a definition at file scope (the namespace scope that contains Friendly in this case). That definition appears after the definition of the function h( ). The linking of the call to f( ) inside h( ) to the same function is a separate matter, however. This is resolved by ADL. Since the argument of f( ) inside h( ) is a Friendly object, the Friendly class is searched for a declaration of f( ), which succeeds. If the call were f(1) instead (which makes some sense since 1 can be implicitly converted to Friendly(1)), the call should fail, since there is no hint of where the compiler should look for the declaration of f( ). The EDG compiler correctly complains that f is undefined in that case.
Now suppose that Friendly and f are both templates, as in the following program:
//: C05:FriendScope2.cpp
#include <iostream>
using namespace std;
// Necessary forward declarations:
template<class T> class Friendly;
template<class T> void f(const
Friendly<T>&);
template<class T> class Friendly {
T t;
public:
Friendly(const T& theT) : t(theT) {}
friend void f<>(const Friendly<T>&);
void g() { f(*this); }
};
void h() {
f(Friendly<int>(1));
}
template<class T> void f(const
Friendly<T>& fo) {
cout << fo.t << endl;
}
int main() {
h();
Friendly<int>(2).g();
} ///:~First notice that angle brackets in the declaration of f inside Friendly. This is necessary to tell the compiler that f is a template. Otherwise, the compiler will look for an ordinary function named f and not find it. We could have inserted the template parameter (<T>) in the brackets, but it is easily deduced from the declaration.
The forward declaration of the function template f before the class definition is necessary, even though it wasn't in the previous example when f was a not a template; the language specifies that friend function templates must be previously declared. To properly declare f, Friendly must also have been declared, since f takes a Friendly argument, hence the forward declaration of Friendly in the beginning. We could have placed the full definition of f right after the initial declaration of Friendly instead of separating its definition and declaration, but we chose instead to leave it in a form that more closely resembles the previous example.
One last option remains for using friends inside templates: fully define them inside the host class template definition itself. Here is how the previous example would appear with that change:
//: C05:FriendScope3.cpp {-bor}
// Microsoft: use the -Za (ANSI-compliant) option
#include <iostream>
using namespace std;
template<class T> class Friendly {
T t;
public:
Friendly(const T& theT) : t(theT) {}
friend void f(const Friendly<T>& fo) {
cout << fo.t << endl;
}
void g() { f(*this); }
};
void h() {
f(Friendly<int>(1));
}
int main() {
h();
Friendly<int>(2).g();
} ///:~There is an important difference between this and the previous example: f is not a template here, but is an ordinary function. (Remember that angle brackets were necessary before to imply that f( ) was a template.) Every time the Friendly class template is instantiated, a new, ordinary function overload is created that takes an argument of the current Friendly specialization. This is what Dan Saks has called “making new friends.”(68) This is the most convenient way to define friend functions for templates.
To clarify, suppose you want to add non-member friend operators to a class template. Here is a class template that simply holds a generic value:
template<class T> class Box {
T t;
public:
Box(const T& theT) : t(theT) {}
};Without understanding the previous examples in this section, novices find themselves frustrated because they can't get a simple stream output inserter to work. If you don't define your operators inside the definition of Box, you must provide the forward declarations we showed earlier:
//: C05:Box1.cpp
// Defines template operators.
#include <iostream>
using namespace std;
// Forward declarations
template<class T> class Box;
template<class T>
Box<T> operator+(const Box<T>&, const
Box<T>&);
template<class T>
ostream& operator<<(ostream&, const
Box<T>&);
template<class T> class Box {
T t;
public:
Box(const T& theT) : t(theT) {}
friend Box operator+<>(const Box<T>&,
const Box<T>&);
friend ostream& operator<< <>(ostream&,
const Box<T>&);
};
template<class T>
Box<T> operator+(const Box<T>& b1,
const Box<T>& b2) {
return Box<T>(b1.t + b2.t);
}
template<class T>
ostream& operator<<(ostream& os, const
Box<T>& b) {
return os << '[' << b.t << ']';
}
int main() {
Box<int> b1(1), b2(2);
cout << b1 + b2 << endl; // [3]
// cout << b1 + 2 << endl; // No implicit
conversions!
} ///:~Here we are defining both an addition operator and an output stream operator. The main program reveals a disadvantage of this approach: you can't depend on implicit conversions (the expression b1 + 2) because templates do not provide them. Using the in-class, non-template approach is shorter and more robust:
//: C05:Box2.cpp
// Defines non-template operators.
#include <iostream>
using namespace std;
template<class T> class Box {
T t;
public:
Box(const T& theT) : t(theT) {}
friend Box<T> operator+(const Box<T>&
b1,
const Box<T>& b2) {
return Box<T>(b1.t + b2.t);
}
friend ostream&
operator<<(ostream& os, const
Box<T>& b) {
return os << '[' << b.t << ']';
}
};
int main() {
Box<int> b1(1), b2(2);
cout << b1 + b2 << endl; // [3]
cout << b1 + 2 << endl; // [3]
} ///:~Because the operators are normal functions (overloaded for each specialization of Box—just int in this case), implicit conversions are applied as normal; so the expression b1 + 2 is valid.
Note that there's one type in particular that cannot be made a friend of Box, or any other class template for that matter, and that type is T—or rather, the type that the class template is parameterized upon. To the best of our knowledge, there are really no good reasons why this shouldn't be allowed, but as is, the declaration friend class T is illegal, and should not compile.
Friend templates
You can be precise as to which specializations of a template are friends of a class. In the examples in the previous section, only the specialization of the function template f with the same type that specialized Friendly was a friend. For example, only the specialization f<int>(const Friendly<int>&) is a friend of the class Friendly<int>. This was accomplished by using the template parameter for Friendly to specialize f in its friend declaration. If we had wanted to, we could have made a particular, fixed specialization of f a friend to all instances of Friendly, like this:
// Inside Friendly:
friend void f<>(const Friendly<double>&);By using double instead of T, the double specialization of f has access to the non-public members of any Friendly specialization. The specialization f<double>( ) still isn't instantiated unless it is explicitly called.
Likewise, if you declare a non-template function with no parameters dependent on T, that single function is a friend to all instances of Friendly:
// Inside Friendly:
friend void g(int); // g(int) befriends all FriendlysAs always, since g(int) is unqualified, it must be defined at file scope (the namespace scope containing Friendly).
It is also possible to arrange for all specializations of f to be friends for all specializations of Friendly, with a so-called friend template, as follows:
template<class T> class Friendly {
template<class U> friend void f<>(const Friendly<U>&);Since the template argument for the friend declaration is independent of T, any combination of T and U is allowed, achieving the friendship objective. Like member templates, friend templates can appear within non-template classes as well.
2-3-5. Template programming idioms▲
Since language is a tool of thought, new language features tend to spawn new programming techniques. In this section we cover some commonly used template programming idioms that have emerged in the years since templates were added to the C++ language.(69)
2-3-5-1. Traits▲
The traits template technique, pioneered by Nathan Myers, is a means of bundling type-dependent declarations together. In essence, using traits you can “mix and match” certain types and values with contexts that use them in a flexible manner, while keeping your code readable and maintainable.
The simplest example of a traits template is the numeric_limits class template defined in <limits>. The primary template is defined as follows:
template<class T> class numeric_limits {
public:
static const bool is_specialized = false;
static T min() throw();
static T max() throw();
static const int digits = 0;
static const int digits10 = 0;
static const bool is_signed = false;
static const bool is_integer = false;
static const bool is_exact = false;
static const int radix = 0;
static T epsilon() throw();
static T round_error() throw();
static const int min_exponent = 0;
static const int min_exponent10 = 0;
static const int max_exponent = 0;
static const int max_exponent10 = 0;
static const bool has_infinity = false;
static const bool has_quiet_NaN = false;
static const bool has_signaling_NaN = false;
static const float_denorm_style has_denorm =
denorm_absent;
static const bool has_denorm_loss = false;
static T infinity() throw();
static T quiet_NaN() throw();
static T signaling_NaN() throw();
static T denorm_min() throw();
static const bool is_iec559 = false;
static const bool is_bounded = false;
static const bool is_modulo = false;
static const bool traps = false;
static const bool tinyness_before = false;
static const float_round_style round_style =
round_toward_zero;
};The <limits> header defines specializations for all fundamental, numeric types (when the member is_specialized is set to true). To obtain the base for the double version of your floating-point number system, for example, you can use the expression numeric_limits<double>::radix. To find the smallest integer value available, you can use numeric_limits<int>::min( ). Not all members of numeric_limits apply to all fundamental types. (For example, epsilon( ) is only meaningful for floating-point types.)
The values that will always be integral are static data members of numeric_limits. Those that may not be integral, such as the minimum value for float, are implemented as static inline member functions. This is because C++ allows only integral static data member constants to be initialized inside a class definition.
In Chapter 3 you saw how traits are used to control the character-processing functionality used by the string classes. The classes std::string and std::wstring are specializations of the std::basic_string template, which is defined as follows:
template<class charT,
class traits = char_traits<charT>,
class allocator = allocator<charT> >
class
basic_string;The template parameter charT represents the underlying character type, which is usually either char or wchar_t. The primary char_traits template is typically empty, and specializations for char and wchar_t are provided by the standard library. Here is the specification of the specialization char_traits<char> according to the C++ Standard:
template<> struct char_traits<char> {
typedef char char_type;
typedef int int_type;
typedef streamoff off_type;
typedef streampos pos_type;
typedef mbstate_t state_type;
static void assign(char_type& c1, const
char_type& c2);
static bool eq(const char_type& c1, const
char_type& c2);
static bool lt(const char_type& c1, const
char_type& c2);
static int compare(const char_type* s1,
const char_type* s2, size_t n);
static size_t length(const char_type* s);
static const char_type* find(const char_type* s,
size_t n,
const char_type& a);
static char_type* move(char_type* s1,
const char_type* s2, size_t
n);
static char_type* copy(char_type* s1,
const char_type* s2, size_t
n);
static char_type* assign(char_type* s, size_t n,
char_type a);
static int_type not_eof(const int_type& c);
static char_type to_char_type(const int_type& c);
static int_type to_int_type(const char_type& c);
static bool eq_int_type(const int_type& c1,
const int_type& c2);
static int_type eof();
};These functions are used by the basic_string class template for character-based operations common to string processing. When you declare a string variable, such as:
std::string
s;you are actually declaring s as follows (because of the default template arguments in the specification of basic_string):
std::basic_string<char,
std::char_traits<char>,
std::allocator<char> > s;Because the character traits have been separated from the basic_string class template, you can supply a custom traits class to replace std::char_traits. The following example illustrates this flexibility:
//: C05:BearCorner.h
#ifndef BEARCORNER_H
#define BEARCORNER_H
#include <iostream>
using std::ostream;
// Item classes (traits of guests):
class Milk {
public:
friend ostream& operator<<(ostream& os,
const Milk&) {
return os << "Milk";
}
};
class CondensedMilk {
public:
friend ostream&
operator<<(ostream& os, const CondensedMilk
&) {
return os << "Condensed Milk";
}
};
class Honey {
public:
friend ostream& operator<<(ostream& os,
const Honey&) {
return os << "Honey";
}
};
class Cookies {
public:
friend ostream& operator<<(ostream& os,
const Cookies&) {
return os << "Cookies";
}
};
// Guest classes:
class Bear {
public:
friend ostream& operator<<(ostream& os,
const Bear&) {
return os << "Theodore";
}
};
class Boy {
public:
friend ostream& operator<<(ostream& os,
const Boy&) {
return os << "Patrick";
}
};
// Primary traits template (empty-could hold common
types)
template<class Guest> class GuestTraits;
// Traits specializations for Guest types
template<> class GuestTraits<Bear> {
public:
typedef CondensedMilk beverage_type;
typedef Honey snack_type;
};
template<> class GuestTraits<Boy> {
public:
typedef Milk beverage_type;
typedef Cookies snack_type;
};
#endif // BEARCORNER_H ///:~//: C05:BearCorner.cpp
// Illustrates traits classes.
#include <iostream>
#include "BearCorner.h"
using namespace std;
// A custom traits class
class MixedUpTraits {
public:
typedef Milk beverage_type;
typedef Honey snack_type;
};
// The Guest template (uses a traits class)
template<class Guest, class traits =
GuestTraits<Guest> >
class BearCorner {
Guest theGuest;
typedef typename traits::beverage_type beverage_type;
typedef typename traits::snack_type snack_type;
beverage_type bev;
snack_type snack;
public:
BearCorner(const Guest& g) : theGuest(g) {}
void entertain() {
cout << "Entertaining " <<
theGuest
<< " serving " << bev
<< " and " << snack
<< endl;
}
};
int main() {
Boy cr;
BearCorner<Boy> pc1(cr);
pc1.entertain();
Bear pb;
BearCorner<Bear> pc2(pb);
pc2.entertain();
BearCorner<Bear, MixedUpTraits> pc3(pb);
pc3.entertain();
} ///:~In this program, instances of the guest classes Boy and Bear are served items appropriate to their tastes. Boys like milk and cookies, and Bears like condensed milk and honey. This association of guests to items is done via specializations of a primary (empty) traits class template. The default arguments to BearCorner ensure that guests get their proper items, but you can override this by simply providing a class that meets the requirements of the traits class, as we do with the MixedUpTraits class above. The output of this program is:
Entertaining Patrick serving Milk and Cookies
Entertaining Theodore serving Condensed Milk and Honey
Entertaining Theodore serving
Milk and HoneyUsing traits provides two key advantages: (1) it allows flexibility and extensibility in pairing objects with associated attributes or functionality, and (2) it keeps template parameter lists small and readable. If 30 types were associated with a guest, it would be inconvenient to have to specify all 30 arguments directly in each BearCorner declaration. Factoring the types into a separate traits class simplifies things considerably.
The traits technique is also used in implementing streams and locales, as we showed in Chapter 4. An example of iterator traits is found in the header file PrintSequence.h in Chapter 6.
2-3-5-2. Policies▲
If you inspect the char_traits specialization for wchar_t, you'll see that it is practically identical to its char counterpart:
template<> struct char_traits<wchar_t> {
typedef wchar_t char_type;
typedef wint_t int_type;
typedef streamoff off_type;
typedef wstreampos pos_type;
typedef mbstate_t state_type;
static void assign(char_type& c1, const
char_type& c2);
static bool eq(const char_type& c1, const
char_type& c2);
static bool lt(const char_type& c1, const
char_type& c2);
static int compare(const char_type* s1,
const char_type* s2, size_t n);
static size_t length(const char_type* s);
static const char_type* find(const char_type* s,
size_t n,
const char_type& a);
static char_type* move(char_type* s1,
const char_type* s2, size_t
n);
static char_type* copy(char_type* s1,
const char_type* s2, size_t
n);
static char_type* assign(char_type* s, size_t n,
char_type a);
static int_type not_eof(const int_type& c);
static char_type to_char_type(const int_type& c);
static int_type to_int_type(const char_type& c);
static bool eq_int_type(const int_type& c1,
const int_type& c2);
static int_type eof();
};The only real difference between the two versions is the set of types involved (char and int vs. wchar_t and wint_t). The functionality provided is the same.(70) This highlights the fact that traits classes are indeed for traits, and the things that change between related traits classes are usually types and constant values, or fixed algorithms that use type-related template parameters. Traits classes tend to be templates themselves, since the types and constants they contain are seen as characteristics of the primary template parameter(s) (for example, char and wchar_t).
It is also useful to be able to associate functionality with template arguments, so that client programmers can easily customize behavior when they code. The following version of the BearCorner program, for instance, supports different types of entertainment:
//: C05:BearCorner2.cpp
// Illustrates policy classes.
#include <iostream>
#include "BearCorner.h"
using namespace std;
// Policy classes (require a static doAction()
function):
class Feed {
public:
static const char* doAction() { return
"Feeding"; }
};
class Stuff {
public:
static const char* doAction() { return
"Stuffing"; }
};
// The Guest template (uses a policy and a traits
class)
template<class Guest, class Action,
class traits = GuestTraits<Guest> >
class BearCorner {
Guest theGuest;
typedef typename traits::beverage_type beverage_type;
typedef typename traits::snack_type snack_type;
beverage_type bev;
snack_type snack;
public:
BearCorner(const Guest& g) : theGuest(g) {}
void entertain() {
cout << Action::doAction() << "
" << theGuest
<< " with " << bev
<< " and " << snack
<< endl;
}
};
int main() {
Boy cr;
BearCorner<Boy, Feed> pc1(cr);
pc1.entertain();
Bear pb;
BearCorner<Bear, Stuff> pc2(pb);
pc2.entertain();
} ///:~The Action template parameter in the BearCorner class expects to have a static member function named doAction( ), which is used in BearCorner<>::entertain( ). Users can choose Feed or Stuff at will, both of which provide the required function. Classes that encapsulate functionality in this way are referred to as policy classes. The entertainment “policies” are provided above through Feed::doAction( ) and Stuff::doAction( ). These policy classes happen to be ordinary classes, but they can be templates, and can be combined with inheritance to great advantage. For more in-depth information on policy-based design, see Andrei Alexandrescu's book,(71) the definitive source on the subject.
2-3-5-3. The curiously recurring template pattern▲
Any novice C++ programmer can figure out how to modify a class to keep track of the number of objects of that class that currently exist. All you have to do is to add static members, and modify constructor and destructor logic, as follows:
//: C05:CountedClass.cpp
// Object counting via static members.
#include <iostream>
using namespace std;
class CountedClass {
static int count;
public:
CountedClass() { ++count; }
CountedClass(const CountedClass&) { ++count; }
~CountedClass() { --count; }
static int getCount() { return count; }
};
int CountedClass::count = 0;
int main() {
CountedClass a;
cout << CountedClass::getCount() <<
endl; // 1
CountedClass b;
cout << CountedClass::getCount() <<
endl; // 2
{ // An arbitrary scope:
CountedClass c(b);
cout << CountedClass::getCount() <<
endl; // 3
a = c;
cout << CountedClass::getCount() <<
endl; // 3
}
cout << CountedClass::getCount() <<
endl; // 2
} ///:~All constructors of CountedClass increment the static data member count, and the destructor decrements it. The static member function getCount( ) yields the current number of objects.
It would be tedious to manually add these members every time you wanted to add object counting to a class. The usual object-oriented device used to repeat or share code is inheritance, which is only half a solution in this case. Observe what happens when we collect the counting logic into a base class.
//: C05:CountedClass2.cpp
// Erroneous attempt to count objects.
#include <iostream>
using namespace std;
class Counted {
static int count;
public:
Counted() { ++count; }
Counted(const Counted&) { ++count; }
~Counted() { --count; }
static int getCount() { return count; }
};
int Counted::count = 0;
class CountedClass : public Counted {};
class CountedClass2 : public Counted {};
int main() {
CountedClass a;
cout << CountedClass::getCount() <<
endl; // 1
CountedClass b;
cout << CountedClass::getCount() <<
endl; // 2
CountedClass2 c;
cout << CountedClass2::getCount() <<
endl; // 3 (Error)
} ///:~All classes that derive from Counted share the same, single static data member, so the number of objects is tracked collectively across all classes in the Counted hierarchy. What is needed is a way to automatically generate a different base class for each derived class. This is accomplished by the curious template construct illustrated below:
//: C05:CountedClass3.cpp
#include <iostream>
using namespace std;
template<class T> class Counted {
static int count;
public:
Counted() { ++count; }
Counted(const Counted<T>&) { ++count; }
~Counted() { --count; }
static int getCount() { return count; }
};
template<class T> int Counted<T>::count =
0;
// Curious class definitions
class CountedClass : public Counted<CountedClass>
{};
class CountedClass2 : public
Counted<CountedClass2> {};
int main() {
CountedClass a;
cout << CountedClass::getCount() <<
endl; // 1
CountedClass b;
cout << CountedClass::getCount() <<
endl; // 2
CountedClass2 c;
cout << CountedClass2::getCount() <<
endl; // 1 (!)
} ///:~Each derived class derives from a unique base class that is determined by using itself (the derived class) as a template parameter! This may seem like a circular definition, and it would be, had any base class members used the template argument in a computation. Since no data members of Counted are dependent on T, the size of Counted (which is zero!) is known when the template is parsed. So it doesn't matter which argument is used to instantiate Counted because the size is always the same. Any derivation from an instance of Counted can be completed when it is parsed, and there is no recursion. Since each base class is unique, it has its own static data, thus constituting a handy technique for adding counting to any class whatsoever. Jim Coplien was the first to mention this interesting derivation idiom in print, which he cited in an article, entitled “Curiously Recurring Template Patterns.” (72)
2-3-6. Template metaprogramming▲
In 1993 compilers were beginning to support simple template constructs so that users could define generic containers and functions. About the same time that the STL was being considered for adoption into Standard C++, clever and surprising examples such as the following were passed around among members of the C++ Standards Committee:(73)
//: C05:Factorial.cpp
// Compile-time computation using templates.
#include <iostream>
using namespace std;
template<int n> struct Factorial {
enum { val = Factorial<n-1>::val * n };
};
template<> struct Factorial<0> {
enum { val = 1 };
};
int main() {
cout << Factorial<12>::val << endl;
// 479001600
} ///:~That this program prints the correct value of 12! is not alarming. What is alarming is that the computation is complete before the program even runs!
When the compiler attempts to instantiate Factorial<12>, it finds it must also instantiate Factorial<11>, which requires Factorial<10>, and so on. Eventually the recursion ends with the specialization Factorial<1>, and the computation unwinds. Eventually, Factorial<12>::val is replaced by the integral constant 479001600, and compilation ends. Since all the computation is done by the compiler, the values involved must be compile-time constants, hence the use of enum. When the program runs, the only work left to do is print that constant followed by a newline. To convince yourself that a specialization of Factorial results in the correct compile-time value, you could use it as an array dimension, such as:
double nums[Factorial<5>::val];
assert(sizeof
nums == sizeof(double)*120);2-3-6-1. Compile-time programming▲
So what was meant to be a convenient way to perform type parameter substitution turned out to be a mechanism to support compile-time programming. Such a program is called a template metaprogram (since you're in effect “programming a program”), and it turns out that you can do quite a lot with it. In fact, template metaprogramming is Turing complete because it supports selection (if-else) and looping (through recursion). Theoretically, then, you can perform any computation with it.(74) The factorial example above shows how to implement repetition: write a recursive template and provide a stopping criterion via a specialization. The following example shows how to compute Fibonacci numbers at compile time by the same technique:
//: C05:Fibonacci.cpp
#include <iostream>
using namespace std;
template<int n> struct Fib {
enum { val = Fib<n-1>::val +
Fib<n-2>::val };
};
template<> struct Fib<1> { enum { val = 1 };
};
template<> struct
Fib<0> { enum { val = 0 }; };
int main() {
cout << Fib<5>::val << endl; // 6
cout << Fib<20>::val << endl; //
6765
} ///:~Fibonacci numbers are defined mathematically as:
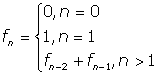
The first two cases lead to the template specializations above, and the rule in the third line becomes the primary template.
Compile-time looping
To compute any loop in a template metaprogram, it must first be reformulated recursively. For example, to raise the integer n to the power p, instead of using a loop such as in the following lines:
int val = 1;
while(p--)
val *=
n;you cast it as a recursive procedure:
int power(int n, int p) {
return (p == 0) ? 1 : n*power(n, p - 1);
}This can now be easily rendered as a template metaprogram:
//: C05:Power.cpp
#include <iostream>
using namespace std;
template<int N, int P> struct Power {
enum { val = N * Power<N, P-1>::val };
};
template<int N> struct Power<N, 0> {
enum { val = 1 };
};
int main() {
cout << Power<2, 5>::val << endl;
// 32
} ///:~We need to use a partial specialization for the stopping condition, since the value N is still a free template parameter. Note that this program only works for non-negative powers.
The following metaprogram adapted from Czarnecki and Eisenecker(75) is interesting in that it uses a template template parameter, and simulates passing a function as a parameter to another function, which “loops through” the numbers 0..n:
//: C05:Accumulate.cpp
// Passes a "function" as a parameter at
compile time.
#include <iostream>
using namespace std;
// Accumulates the results of F(0)..F(n)
template<int n, template<int> class F> struct
Accumulate {
enum { val = Accumulate<n-1, F>::val +
F<n>::val };
};
// The stopping criterion (returns the value F(0))
template<template<int> class F> struct
Accumulate<0, F> {
enum { val = F<0>::val };
};
// Various "functions":
template<int n> struct
Identity {
enum { val = n };
};
template<int n> struct Square {
enum { val = n*n };
};
template<int n> struct Cube {
enum { val = n*n*n };
};
int main() {
cout << Accumulate<4, Identity>::val
<< endl; // 10
cout << Accumulate<4, Square>::val
<< endl; // 30
cout << Accumulate<4, Cube>::val <<
endl; // 100
} ///:~The primary Accumulate template attempts to compute the sum F(n)+F(n‑1)…F(0). The stopping criterion is obtained by a partial specialization, which “returns” F(0). The parameter F is itself a template, and acts like a function as in the previous examples in this section. The templates Identity, Square, and Cube compute the corresponding functions of their template parameter that their names suggest. The first instantiation of Accumulate in main( ) computes the sum 4+3+2+1+0, because the Identity function simply “returns” its template parameter. The second line in main( ) adds the squares of those numbers (16+9+4+1+0), and the last computes the sum of the cubes (64+27+8+1+0).
Loop unrolling
Algorithm designers have always endeavored to optimize their programs. One time-honored optimization, especially for numeric programming, is loop unrolling, a technique that minimizes loop overhead. The quintessential loop-unrolling example is matrix multiplication. The following function multiplies a matrix and a vector. (Assume that the constants ROWS and COLS have been previously defined.):
void mult(int a[ROWS][COLS], int x[COLS], int y[COLS])
{
for(int i = 0; i < ROWS; ++i) {
y[i] = 0;
for(int j = 0; j < COLS; ++j)
y[i] += a[i][j]*x[j];
}
}If COLS is an even number, the overhead of incrementing and comparing the loop control variable j can be cut in half by “unrolling” the computation into pairs in the inner loop:
void mult(int a[ROWS][COLS], int x[COLS], int y[COLS])
{
for(int i = 0; i < ROWS; ++i) {
y[i] = 0;
for(int j = 0; j < COLS; j += 2)
y[i] += a[i][j]*x[j] + a[i][j+1]*x[j+1];
}
}In general, if COLS is a factor of k, k operations can be performed each time the inner loop iterates, greatly reducing the overhead. The savings is only noticeable on large arrays, but that is precisely the case with industrial-strength mathematical computations.
Function inlining also constitutes a form of loop unrolling. Consider the following approach to computing powers of integers:
//: C05:Unroll.cpp
// Unrolls an implicit loop via inlining.
#include <iostream>
using namespace std;
template<int n> inline int power(int m) {
return power<n-1>(m) * m;
}
template<> inline int power<1>(int m) {
return m;
}
template<> inline int power<0>(int m) {
return 1;
}
int main() {
int m = 4;
cout << power<3>(m) << endl;
} ///:~Conceptually, the compiler must generate three specializations of power<>, one each for the template parameters 3, 2, and 1. Because the code for each of these functions can be inlined, the actual code that is inserted into main( ) is the single expression m*m*m. Thus, a simple template specialization coupled with inlining provides a way to totally avoid loop control overhead.(76) This approach to loop unrolling is limited by your compiler's inlining depth.
Compile-time selection
To simulate conditionals at compile time, you can use the conditional ternary operator in an enum declaration. The following program uses this technique to calculate the maximum of two integers at compile time:
//: C05:Max.cpp
#include <iostream>
using namespace std;
template<int n1, int n2> struct Max {
enum { val = n1 > n2 ? n1 : n2 };
};
int main() {
cout << Max<10, 20>::val << endl;
// 20
} ///:~If you want to use compile-time conditions to govern custom code generation, you can use specializations of the values true and false:
//: C05:Conditionals.cpp
// Uses compile-time conditions to choose code.
#include <iostream>
using namespace std;
template<bool cond> struct Select {};
template<> class Select<true> {
static void statement1() {
cout << "This is statement1 executing\n";
}
public:
static void f() { statement1(); }
};
template<> class Select<false> {
static void statement2() {
cout << "This is statement2
executing\n";
}
public:
static void f() { statement2(); }
};
template<bool cond> void execute() {
Select<cond>::f();
}
int main() {
execute<sizeof(int) == 4>();
} ///:~This program is equivalent to the expression:
if(cond)
statement1();
else
statement2();except that the condition cond is evaluated at compile time, and the appropriate versions of execute<>( ) and Select<> are instantiatedby the compiler. The function Select<>::f( ) executes at runtime. A switch statement can be emulated in similar fashion, but specializing on each case value instead of the values true and false.
Compile-time assertions
In Chapter 2 we touted the virtues of using assertions as part of an overall defensive programming strategy. An assertion is basically an evaluation of a Boolean expression followed by a suitable action: do nothing if the condition is true, or halt with a diagnostic message otherwise. It's best to discover assertion failures as soon as possible. If you can evaluate an expression at compile time, use a compile-time assertion. The following example uses a technique that maps a Boolean expression to an array declaration:
//: C05:StaticAssert1.cpp {-xo}
// A simple, compile-time assertion facility
#define STATIC_ASSERT(x) \
do { typedef int a[(x) ? 1 : -1]; } while(0)
int main() {
STATIC_ASSERT(sizeof(int) <= sizeof(long)); //
Passes
STATIC_ASSERT(sizeof(double) <= sizeof(int)); //
Fails
} ///:~The do loop creates a temporary scope for the definition of an array, a, whose size is determined by the condition in question. It is illegal to define an array of size -1, so when the condition is false the statement should fail.
The previous section showed how to evaluate compile-time Boolean expressions. The remaining challenge in emulating assertions at compile time is to print a meaningful error message and halt. All that is required to halt the compiler is a compile error; the trick is to insert helpful text in the error message. The following example from Alexandrescu(77) uses template specialization, a local class, and a little macro magic to do the job:
//: C05:StaticAssert2.cpp {-g++}
#include <iostream>
using namespace std;
// A template and a specialization
template<bool> struct StaticCheck {
StaticCheck(...);
};
template<> struct StaticCheck<false> {};
// The macro (generates a local class)
#define STATIC_CHECK(expr, msg) { \
class Error_##msg {}; \
sizeof((StaticCheck<expr>(Error_##msg()))); \
}
// Detects narrowing conversions
template<class To, class From> To safe_cast(From
from) {
STATIC_CHECK(sizeof(From) <= sizeof(To),
NarrowingConversion);
return reinterpret_cast<To>(from);
}
int main() {
void* p = 0;
int i = safe_cast<int>(p);
cout << "int cast okay” << endl;
//! char c = safe_cast<char>(p);
} ///:~This example defines a function template, safe_cast<>( ), that checks to see if the object it is casting from is no larger than the type of object it casts to. If the size of the target object type is smaller, then the user will be notified at compile time that a narrowing conversion was attempted. Notice that the StaticCheck class template has the curious feature that anything can be converted to an instance of StaticCheck<true> (because of the ellipsis in its constructor(78)), and nothing can be converted to a StaticCheck<false> because no conversions are supplied for that specialization. The idea is to attempt to create an instance of a new class and attempt to convert it to StaticCheck<true>at compile time whenever the condition of interest is true, or to a StaticCheck<false> object when the condition being tested is false. Since the sizeof operator does its work at compile time, it is used to attempt the conversion. If the condition is false, the compiler will complain that it doesn't know how to convert from the new class type to StaticCheck<false>. (The extra parentheses inside the sizeof invocation in STATIC_CHECK( ) are to prevent the compiler from thinking that we're trying to invoke sizeof on a function, which is illegal.) To get some meaningful information inserted into the error message, the new class name carries key text in its name.
The best way to understand this technique is to walk through a specific case. Consider the line in main( ) above which reads:
int i =
safe_cast<int>(p);The call to safe_cast<int>(p) contains the following macro expansion replacing its first line of code:
{ \
class Error_NarrowingConversion {}; \
sizeof(StaticCheck<sizeof(void*) <= sizeof(int)>
\
(Error_NarrowingConversion())); \
}(Recall that the token-pasting preprocessing operator, ##, concatenates its operand into a single token, so Error_##NarrowingConversion becomes the token Error_NarrowingConversion after preprocessing). The class Error_NarrowingConversion is a local class (meaning that it is declared inside a non-namespace scope) because it is not needed elsewhere in the program. The application of the sizeof operator here attempts to determine the size of an instance of StaticCheck<true> (because sizeof(void*) <= sizeof(int) is true on our platforms), created implicitly from the temporary object returned by the call Error_NarrowingConversion( ). The compiler knows the size of the new class Error_NarrowingConversion (it's empty), and so the compile-time use of sizeof at the outer level in STATIC_CHECK( ) is valid. Since the conversion from the Error_NarrowingConversion temporary to StaticCheck<true> succeeds, so does this outer application of sizeof, and execution continues.
Now consider what would happen if the comment were removed from the last line of main( ):
char c
= safe_cast<char>(p);Here the STATIC_CHECK( ) macro inside safe_cast<char>(p) expands to:
{ \
class Error_NarrowingConversion {}; \
sizeof(StaticCheck<sizeof(void*) <=
sizeof(char)> \
(Error_NarrowingConversion())); \
}Since the expression sizeof(void*) <= sizeof(char) is false, a conversion from an Error_NarrowingConversion temporary to StaticCheck<false> is attempted, as follows:
sizeof(StaticCheck<false>(Error_NarrowingConversion()));which fails, so the compiler halts with a message something like the following:
Cannot cast from
'Error_NarrowingConversion' to 'StaticCheck<0>' in function
char safe_cast<char,void *>(void *)The class name Error_NarrowingConversion is the meaningful message judiciously arranged by the coder. In general, to perform a static assertion with this technique, you just invoke the STATIC_CHECK macro with the compile-time condition to check and with a meaningful name to describe the error.
2-3-6-2. Expression templates▲
Perhaps the most powerful application of templates is a technique discovered independently in 1994 by Todd Veldhuizen(79) and Daveed Vandevoorde:(80) expression templates. Expression templates enable extensive compile-time optimization of certain computations that result in code that is at least as fast as hand-optimized Fortran, and yet preserves the natural notation of mathematics via operator overloading. Although you wouldn't be likely to use this technique in everyday programming, it is the basis for a number of sophisticated, high-performance mathematical libraries written in C++.(81)
To motivate the need for expression templates, consider typical numerical linear algebra operations, such as adding together two matrices or vectors,(82) such as in the following:
D = A + B
+ C;In naive implementations, this expression would result in a number of temporaries—one for A+B, and one for (A+B)+C. When these variables represent immense matrices or vectors, the coincident drain on resources is unacceptable. Expression templates allow you to use the same expression without temporaries.
The following program defines a MyVector class to simulate mathematical vectors of any size. We use a non-type template argument for the length of the vector. We also define a MyVectorSum class to act as a proxy class for a sum of MyVector objects. This allows us to use lazy evaluation, so the addition of vector components is performed on demand without the need for temporaries.
//: C05:MyVector.cpp
// Optimizes away temporaries via templates.
#include <cstddef>
#include <cstdlib>
#include <ctime>
#include <iostream>
using namespace std;
// A proxy class for sums of vectors
template<class, size_t> class MyVectorSum;
template<class T, size_t N> class MyVector {
T data[N];
public:
MyVector<T,N>& operator=(const
MyVector<T,N>& right) {
for(size_t i = 0; i < N; ++i)
data[i] = right.data[i];
return *this;
}
MyVector<T,N>& operator=(const
MyVectorSum<T,N>& right);
const T& operator[](size_t i) const { return
data[i]; }
T& operator[](size_t i) { return data[i]; }
};
// Proxy class hold references; uses lazy addition
template<class T, size_t N> class MyVectorSum {
const MyVector<T,N>& left;
const MyVector<T,N>& right;
public:
MyVectorSum(const MyVector<T,N>& lhs,
const MyVector<T,N>& rhs)
: left(lhs), right(rhs) {}
T operator[](size_t i) const {
return left[i] + right[i];
}
};
// Operator to support v3 = v1 + v2
template<class T, size_t N> MyVector<T,N>&
MyVector<T,N>::operator=(const
MyVectorSum<T,N>& right) {
for(size_t i = 0; i < N; ++i)
data[i] = right[i];
return *this;
}
// operator+ just stores references
template<class T, size_t N> inline
MyVectorSum<T,N>
operator+(const MyVector<T,N>& left,
const MyVector<T,N>& right) {
return MyVectorSum<T,N>(left, right);
}
// Convenience functions for the test program below
template<class T, size_t N> void
init(MyVector<T,N>& v) {
for(size_t i = 0; i < N; ++i)
v[i] = rand() % 100;
}
template<class T, size_t N> void
print(MyVector<T,N>& v) {
for(size_t i = 0; i < N; ++i)
cout << v[i] << ' ';
cout << endl;
}
int main() {
srand(time(0));
MyVector<int, 5> v1;
init(v1);
print(v1);
MyVector<int, 5> v2;
init(v2);
print(v2);
MyVector<int, 5> v3;
v3 = v1 + v2;
print(v3);
MyVector<int, 5> v4;
// Not yet supported:
//! v4 = v1 + v2 + v3;
} ///:~The MyVectorSum class does no computation when it is created; it merely holds references to the two vectors to be added. Calculations happen only when you access a component of a vector sum (see its operator[ ]( )). The overload of the assignment operator for MyVector that takes a MyVectorSum argument is for an expression such as:
v1 = v2 + v3;
// Add two vectorsWhen the expression v1+v2 is evaluated, a MyVectorSum object is returned (or actually, inserted inline, since that operator+( ) is declared inline). This is a small, fixed-size object (it holds only two references). Then the assignment operator mentioned above is invoked:
v3.operator=<int,5>(MyVectorSum<int,5>(v2,
v3));This assigns to each element of v3 the sum of the corresponding elements of v1 and v2, computed in real time. No temporary MyVector objects are created.
This program does not support an expression that has more than two operands, however, such as
v4 = v1 +
v2 + v3;The reason is that, after the first addition, a second addition is attempted:
(v1 + v2) +
v3;which would require an operator+( ) with a first argument of MyVectorSum and a second argument of type MyVector. We could attempt to provide a number of overloads to meet all situations, but it is better to let templates do the work, as in the following version of the program:
//: C05:MyVector2.cpp
// Handles sums of any length with expression templates.
#include <cstddef>
#include <cstdlib>
#include <ctime>
#include <iostream>
using namespace std;
// A proxy class for sums of vectors
template<class, size_t, class, class> class
MyVectorSum;
template<class T, size_t N> class MyVector {
T data[N];
public:
MyVector<T,N>& operator=(const
MyVector<T,N>& right) {
for(size_t i = 0; i < N; ++i)
data[i] = right.data[i];
return *this;
}
template<class Left, class
Right> MyVector<T,N>&
operator=(const
MyVectorSum<T,N,Left,Right>& right);
const T& operator[](size_t i) const {
return data[i];
}
T& operator[](size_t i) {
return data[i];
}
};
// Allows mixing MyVector and MyVectorSum
template<class T, size_t N, class Left, class
Right>
class MyVectorSum {
const Left& left;
const Right& right;
public:
MyVectorSum(const Left& lhs, const Right&
rhs)
: left(lhs), right(rhs) {}
T operator[](size_t i) const {
return left[i] + right[i];
}
};
template<class T, size_t N>
template<class Left, class Right>
MyVector<T,N>&
MyVector<T,N>::
operator=(const MyVectorSum<T,N,Left,Right>&
right) {
for(size_t i = 0; i < N; ++i)
data[i] = right[i];
return *this;
}
// operator+ just stores references
template<class T, size_t N>
inline
MyVectorSum<T,N,MyVector<T,N>,MyVector<T,N> >
operator+(const MyVector<T,N>& left,
const MyVector<T,N>& right) {
return
MyVectorSum<T,N,MyVector<T,N>,MyVector<T,N> >
(left,right);
}
template<class T, size_t N, class Left, class
Right>
inline MyVectorSum<T, N,
MyVectorSum<T,N,Left,Right>,
MyVector<T,N> >
operator+(const MyVectorSum<T,N,Left,Right>&
left,
const MyVector<T,N>& right) {
return
MyVectorSum<T,N,MyVectorSum<T,N,Left,Right>,
MyVector<T,N> >
(left, right);
}
// Convenience functions for the test program below
template<class T, size_t N> void
init(MyVector<T,N>& v) {
for(size_t i = 0; i < N; ++i)
v[i] = rand() % 100;
}
template<class T, size_t N> void
print(MyVector<T,N>& v) {
for(size_t i = 0; i < N; ++i)
cout << v[i] << ' ';
cout << endl;
}
int main() {
srand(time(0));
MyVector<int, 5> v1;
init(v1);
print(v1);
MyVector<int, 5> v2;
init(v2);
print(v2);
MyVector<int, 5> v3;
v3 = v1 + v2;
print(v3);
// Now supported:
MyVector<int, 5> v4;
v4 = v1 + v2 + v3;
print(v4);
MyVector<int, 5> v5;
v5 = v1 + v2 + v3 + v4;
print(v5);
} ///:~The template facility deduces the argument types of a sum using the template arguments, Left and Right, instead of committing to those types ahead of time. The MyVectorSum template takes these extra two parameters so it can represent a sum of any combination of pairs of MyVector and MyVectorSum.
The assignment operator is now a member function template. This allows any <T, N> pair to be coupled with any <Left,Right> pair, so a MyVector object can be assigned from a MyVectorSum holding references to any possible pair of the types MyVector and MyVectorSum.
As we did before, let's trace through a sample assignment to understand exactly what takes place, beginning with the expression
v4 = v1 +
v2 + v3;Since the resulting expressions become quite unwieldy, in the explanation that follows, we will use MVS as shorthand for MyVectorSum, and will omit the template arguments.
The first operation is v1+v2, which invokes the inline operator+( ), which in turn inserts MVS(v1, v2) into the compilation stream. This is then added to v3, which results in a temporary object according to the expression MVS(MVS(v1, v2), v3). The final representation of the entire statement is
v4.operator+(MVS(MVS(v1,
v2), v3));This transformation is all arranged by the compiler and explains why this technique carries the moniker “expression templates.” The template MyVectorSum represents an expression (an addition, in this case), and the nested calls above are reminiscent of the parse tree of the left-associative expression v1+v2+v3.
An excellent article by Angelika Langer and Klaus Kreft explains how this technique can be extended to more complex computations.(83)
2-3-7. Template compilation models▲
You may have noticed that all our template examples place fully-defined templates within each compilation unit. (For example, we place them completely within single-file programs, or in header files for multi-file programs.) This runs counter to the conventional practice of separating ordinary function definitions from their declarations by placing the latter in header files and the function implementations in separate (that is, .cpp) files.
The reasons for this traditional separation are:
- Non-inline function bodies in header files lead to multiple function definitions, resulting in linker errors.
- Hiding the implementation from clients helps reduce compile-time coupling.
- Vendors can distribute pre-compiled code (for a particular compiler) along with headers so that users cannot see the function implementations.
- Compile times are shorter since header files are smaller.
2-3-7-1. The inclusion model▲
Templates, on the other hand, are not code per se, but instructions for code generation. Only template instantiations are real code. When a compiler has seen a complete template definition during a compilation and then encounters a point of instantiation for that template in the same translation unit, it must deal with the fact that an equivalent point of instantiation may be present in another translation unit. The most common approach consists of generating the code for the instantiation in every translation unit and letting the linker weed out duplicates. That particular approach also works well with inline functions that cannot be inlined and with virtual function tables, which is one of the reasons for its popularity. Nonetheless, several compilers prefer instead to rely on more complex schemes to avoid generating a particular instantiation more than once. Either way, it is the responsibility of the C++ translation system to avoid errors due to multiple equivalent points of instantiation.
A drawback of this approach is that all template source code is visible to the client, so there is little opportunity for library vendors to hide their implementation strategies. Another disadvantage of the inclusion model is that header files are much larger than they would be if function bodies were compiled separately. This can increase compile times dramatically over traditional compilation models.
To help reduce the large headers required by the inclusion model, C++ offers two (non-exclusive) alternative code organization mechanisms: you can manually instantiate each specialization using explicit instantiation or you can use exported templates, which support a large degree of separate compilation.
2-3-7-2. Explicit instantiation▲
You can manually direct the compiler to instantiate any template specializations of your choice. When you use this technique, there must be one and only one such directive for each such specialization; otherwise you mightget multiple definition errors, just as you would with ordinary, non-inline functions with identical signatures. To illustrate, we first (erroneously) separate the declaration of the min( ) template from earlier in this chapter from its definition, following the normal pattern for ordinary, non-inline functions. The following example consists of five files:
- OurMin.h: contains the declaration of the min( ) function template.
- OurMin.cpp: contains the definition of the min( ) function template.
- UseMin1.cpp: attempts to use an int-instantiation of min( ).
- UseMin2.cpp: attempts to use a double-instantiation of min( ).
- MinMain.cpp: calls usemin1( ) and usemin2( ).
//: C05:OurMin.h
#ifndef OURMIN_H
#define OURMIN_H
// The declaration of min()
template<typename T> const T& min(const
T&, const T&);
#endif //
OURMIN_H ///:~// OurMin.cpp
#include "OurMin.h"
// The definition of min()
template<typename T> const T& min(const
T& a, const T& b) {
return (a < b) ? a : b;
}//: C05:UseMin1.cpp {O}
#include <iostream>
#include "OurMin.h"
void usemin1() {
std::cout << min(1,2) <<
std::endl;
} ///:~//: C05:UseMin2.cpp {O}
#include <iostream>
#include "OurMin.h"
void usemin2() {
std::cout << min(3.1,4.2)
<< std::endl;
} ///:~//: C05:MinMain.cpp
//{L} UseMin1 UseMin2 MinInstances
void usemin1();
void usemin2();
int main() {
usemin1();
usemin2();
} ///:~When we attempt to build this program, the linker reports unresolved external references for min<int>( ) and min<double>( ). The reason is that when the compiler encounters the calls to specializations of min( ) in UseMin1 and UseMin2, only the declaration of min( ) is visible. Since the definition is not available, the compiler assumes it will come from some other translation unit, and the needed specializations are thus not instantiated at that point, leaving the linker to eventually complain that it cannot find them.
To solve this problem, we will introduce a new file, MinInstances.cpp, that explicitly instantiates the needed specializations of min( ):
//: C05:MinInstances.cpp {O}
#include "OurMin.cpp"
// Explicit Instantiations for int and double
template const int& min<int>(const int&,
const int&);
template const double& min<double>(const
double&,
const double&);
///:~To manually instantiate a particular template specialization, you precede the specialization's declaration with the template keyword. Note that we must include OurMin.cpp, not OurMin.h, here, because the compiler needs the template definition to perform the instantiation. This is the only place where we have to do this in this program,(84) however, since it gives us the unique instantiations of min( ) that we need—the declarations alone suffice for the other files. Since we are including OurMin.cpp with the macro preprocessor, we add include guards:
//: C05:OurMin.cpp {O}
#ifndef OURMIN_CPP
#define OURMIN_CPP
#include "OurMin.h"
template<typename T> const T& min(const
T& a, const T& b) {
return (a < b) ? a : b;
}
#endif //
OURMIN_CPP ///:~Now when we compile all the files together into a complete program, the unique instances of min( ) are found, and the program executes correctly, giving the output:
1
3.1You can also manually instantiate classes and static data members. When explicitly instantiating a class, all member functions for the requested specialization are instantiated, except any that may have been explicitly instantiated previously. This is important, as it will render many templates useless when using this mechanism—specifically, templates that implement different functionality depending on their parameterization type. Implicit instantiation has the advantage here: only member functions that get called are instantiated.
Explicit instantiation is intended for large projects where a hefty chunk of compilation time can be avoided. Whether you use implicit or explicit instantiation is independent of which template compilation you use. You can use manual instantiation with either the inclusion model or the separation model (discussed in the next section).
2-3-7-3. The separation model▲
The separation model of template compilation separates function template definitions or static data member definitions from their declarations across translation units, just like you do with ordinary functions and data, by exporting templates. After reading the preceding two sections, this must sound strange. Why bother to have the inclusion model in the first place if you can just adhere to the status quo? The reasons are both historical and technical.
Historically, the inclusion model was the first to experience widespread commercial use—all C++ compilers support the inclusion model. Part of the reason for that was that the separation model was not well specified until late in the standardization process, but also that the inclusion model is easier to implement. A lot of working code was in existence long before the semantics of the separation model were finalized.
The separation model is so difficult to implement that, as of Summer 2003, only one compiler front end (EDG) supports the separation model, and at the moment it still requires that template source code be available at compile time to perform instantiation on demand. Plans are in place to use some form of intermediate code instead of requiring that the original source be at hand, at which point you will be able to ship “pre-compiled” templates without shipping source code. Because of the lookup complexities explained earlier in this chapter (about dependent names being looked up in the template definition context), a full template definition still has to be available in some form when you compile a program that instantiates it.
The syntax to separate the source code of a template definition from its declaration is easy enough. You use the export keyword:
// C05:OurMin2.h
// Declares min as an exported template
// (Only works with EDG-based compilers)
#ifndef OURMIN2_H
#define OURMIN2_H
export template<typename T> const T&
min(const T&,
const T&);
#endif //
OURMIN2_H ///:~Similar to inline or virtual, the export keyword need only be mentioned once in a compilation stream, where an exported template is introduced. For this reason, we need not repeat it in the implementation file, but it is considered good practice to do so:
// C05:OurMin2.cpp
// The definition of the exported min template
// (Only works with EDG-based compilers)
#include "OurMin2.h"
export
template<typename T> const T& min(const
T& a, const T& b) {
return (a < b) ? a : b;
} ///:~The UseMin files used previously only need to include the correct header file (OurMin2.h), and the main program doesn't change. Although this appears to give true separation, the file with the template definition (OurMin2.cpp) must still be shipped to users (because it must be processed for each instantiation of min( )) until such time as some form of intermediate code representation of template definitions is supported. So while the standard does provide for a true separation model, not all of its benefits can be reaped today. Only one family of compilers currently supports export (those based on the EDG front end), and these compilers currently do not exploit the potential ability to distribute template definitions in compiled form.
2-3-8. Summary▲
Templates go far beyond simple type parameterization. When you combine argument type deduction, custom specialization, and template metaprogramming, C++ templates emerge as a powerful code generation mechanism.
One of the weaknesses of C++ templates that we did not mention is the difficulty in interpreting compile-time error messages. The quantity of inscrutable text spewed out by the compiler can be quite overwhelming. C++ compilers have improved their template error messages, and Leor Zolman has written a tool called STLFilt that renders these error messages much more readable by extracting the useful information and throwing away the rest.(85)
Another important idea to take away from this chapter is that a template implies an interface. That is, even though the template keyword says “I'll take any type,” the code in a template definition requires that certain operators and member functions be supported—that's the interface. So in reality, a template definition is saying, “I'll take any type that supports this interface.” Things would be much nicer if the compiler could simply say, “Hey, this type that you're trying to instantiate the template with doesn't support that interface—can't do it.” Using templates constitutes a sort of “latent type checking” that is more flexible than the pure object-oriented practice of requiring all types to derive from certain base classes.
In Chapters 6 and 7 we explore in depth the most famous application of templates, the subset of the Standard C++ library commonly known as the Standard Template Library (STL). Chapters 9 and 10 also use template techniques not found in this chapter.
2-3-9. Exercises▲
Solutions to selected exercises can be found in the electronic document The Thinking in C++ Volume 2 Annotated Solution Guide, available for a small fee from www.MindView.net.
- Write a unary function template that takes a single type template parameter. Create a full specialization for the type int. Also create a non-template overload for this function that takes a single int parameter. Have your main program invoke three function variations.
- Write a class template that uses a vector to implement a stack data structure.
- Modify your solution to the previous exercise so that the type of the container used to implement the stack is a template template parameter.
- In the following code, the class NonComparable does not
have an operator=( ). Why would the presence of the class HardLogic
cause a compile error, but SoftLogic would not?
Sélectionnez
//: C05:Exercise4.cpp {-xo}classNoncomparable{};structHardLogic{Noncomparable nc1, nc2;voidcompare(){returnnc1==nc2;// Compiler error}};template<classT>structSoftLogic{Noncomparable nc1, nc2;voidnoOp(){}voidcompare(){nc1==nc2;}};intmain(){SoftLogic<Noncomparable>l; l.noOp();}///:~ - Write a function template that takes a single type parameter (T) and accepts four function arguments: an array of T, a start index, a stop index (inclusive), and an optional initial value. The function returns the sum of all the array elements in the specified range and the initial value. Use the default constructor of T for the default initial value.
- Repeat the previous exercise but use explicit instantiation to manually create specializations for int and double, following the technique explained in this chapter.
- Why does the following code not compile? (Hint: what do class
member functions have access to?)
Sélectionnez
//: C05:Exercise7.cpp {-xo}classBuddy{};template<classT>classMy{inti;public:voidplay(My<Buddy>&s){s.i=3;}};intmain(){My<int>h; My<Buddy>me, bud; h.play(bud); me.play(bud);}///:~ - Why does the following code not compile?
Sélectionnez
//: C05:Exercise8.cpp {-xo}template<classT>doublepythag(T a, T b, T c){return(-b+sqrt(double(b*b-4*a*c)))/2*a;}intmain(){pythag(1,2,3); pythag(1.0,2.0,3.0); pythag(1,2.0,3.0); pythag<double>(1,2.0,3.0);}///:~ - Write templates that take non-type parameters of the following variety: an int, a pointer to an int, a pointer to a static class member of type int, and a pointer to a static member function.
- Write a class template that takes two type parameters. Define a partial specialization for the first parameter, and another partial specialization that specifies the second parameter. In each specialization, introduce members that are not in the primary template.
- Define a class template named Bob that takes a single type parameter. Make Bob a friend of all instances of a template class named Friendly, and a friend of a class template named Picky only when the type parameter of Bob and Picky are identical. Give Bob member functions that demonstrate its friendship.
2-4. Generic Algorithms▲
Algorithms are at the core of computing. To be able to write an algorithm that works with any type of sequence makes your programs both simpler and safer. The ability to customize algorithms at runtime has revolutionized software development.
The subset of the Standard C++ library known as the Standard Template Library (STL) was originally designed around generic algorithms—code that processes sequences of any type of values in a type-safe manner. The goal was to use predefined algorithms for almost every task, instead of hand-coding loops every time you need to process a collection of data. This power comes with a bit of a learning curve, however. By the time you get to the end of this chapter, you should be able to decide for yourself whether you find the algorithms addictive or too confusing to remember. If you're like most people, you'll resist them at first but then tend to use them more and more as time goes on.
2-4-1. A first look▲
Among other things, the generic algorithms in the standard library provide a vocabulary with which to describe solutions. Once you become familiar with the algorithms, you'll have a new set of words with which to discuss what you're doing, and these words are at a higher level than what you had before. You don't need to say, “This loop moves through and assigns from here to there … oh, I see, it's copying!” Instead, you just say copy( ). This is what we've been doing in computer programming from the beginning—creating high-level abstractions to express what you're doing and spending less time saying how you're doing it. The how has been solved once and for all and is hidden in the algorithm's code, ready to be reused on demand.
Here's an example of how to use the copy algorithm:
//: C06:CopyInts.cpp
// Copies ints without an explicit loop.
#include <algorithm>
#include <cassert>
#include <cstddef> // For size_t
using namespace std;
int main() {
int a[] = { 10, 20, 30 };
const size_t SIZE = sizeof a / sizeof a[0];
int b[SIZE];
copy(a, a + SIZE, b);
for(size_t i = 0; i < SIZE; ++i)
assert(a[i] == b[i]);
} ///:~The copy( ) algorithm's first two parameters represent the range of the input sequence—in this case the array a. Ranges are denoted by a pair of pointers. The first points to the first element of the sequence, and the second points one position past the end of the array (right after the last element). This may seem strange at first, but it is an old C idiom that comes in quite handy. For example, the difference of these two pointers yields the number of elements in the sequence. More important, in implementing copy, the second pointer can act as a sentinel to stop the iteration through the sequence. The third argument refers to the beginning of the output sequence, which is the array b in this example. It is assumed that the array that b represents has enough space to receive the copied elements.
The copy( ) algorithm wouldn't be very exciting if it could only process integers. It can copy any kind of sequence. The following example copies string objects:
//: C06:CopyStrings.cpp
// Copies strings.
#include <algorithm>
#include <cassert>
#include <cstddef>
#include <string>
using namespace std;
int main() {
string a[] = {"read", "my",
"lips"};
const size_t SIZE = sizeof a / sizeof a[0];
string b[SIZE];
copy(a, a + SIZE, b);
assert(equal(a, a + SIZE, b));
} ///:~This example introduces another algorithm, equal( ), which returns true only if each element in the first sequence is equal (using its operator==( )) to the corresponding element in the second sequence. This example traverses each sequence twice, once for the copy, and once for the comparison, without a single explicit loop!
Generic algorithms achieve this flexibility because they are function templates. If you think that the implementation of copy( ) looks like the following, you're almost right:
template<typename T> void copy(T* begin, T* end,
T* dest) {
while(begin != end)
*dest++ = *begin++;
}We say “almost” because copy( ) can process sequences delimited by anything that acts like a pointer, such as an iterator. In this way, copy( ) can be used to duplicate a vector:
//: C06:CopyVector.cpp
// Copies the contents of a vector.
#include <algorithm>
#include <cassert>
#include <cstddef>
#include <vector>
using namespace std;
int main() {
int a[] = { 10, 20, 30 };
const size_t SIZE = sizeof a / sizeof a[0];
vector<int> v1(a, a + SIZE);
vector<int> v2(SIZE);
copy(v1.begin(), v1.end(), v2.begin());
assert(equal(v1.begin(), v1.end(), v2.begin()));
} ///:~The first vector, v1, is initialized from the sequence of integers in the array a. The definition of the vectorv2 uses a different vector constructor that makes room for SIZE elements, initialized to zero (the default value for integers).
As with the array example earlier, it's important that v2 have enough space to receive a copy of the contents of v1. For convenience, a special library function, back_inserter( ), returns a special type of iterator that inserts elements instead of overwriting them, so memory is expanded automatically by the container as needed. The following example uses back_inserter( ), so it doesn't have to establish the size of the output vector, v2, ahead of time:
//: C06:InsertVector.cpp
// Appends the contents of a vector to another.
#include <algorithm>
#include <cassert>
#include <cstddef>
#include <iterator>
#include <vector>
using namespace std;
int main() {
int a[] = { 10, 20, 30 };
const size_t SIZE = sizeof a / sizeof a[0];
vector<int> v1(a, a + SIZE);
vector<int> v2; // v2 is empty here
copy(v1.begin(), v1.end(), back_inserter(v2));
assert(equal(v1.begin(), v1.end(), v2.begin()));
} ///:~The back_inserter( ) function is defined in the <iterator> header. We'll explain how insert iterators work in depth in the next chapter.
Since iterators are identical to pointers in all essential ways, you can write the algorithms in the standard library in such a way as to allow both pointer and iterator arguments. For this reason, the implementation of copy( ) looks more like the following code:
template<typename Iterator>
void copy(Iterator begin, Iterator end, Iterator dest)
{
while(begin != end)
*begin++ = *dest++;
}Whichever argument type you use in the call, copy( ) assumes it properly implements the indirection and increment operators. If it doesn't, you'll get a compile-time error.
2-4-1-1. Predicates▲
At times, you might want to copy only a well-defined subset of one sequence to another, such as only those elements that satisfy a particular condition. To achieve this flexibility, many algorithms have alternate calling sequences that allow you to supply a predicate, which is simply a function that returns a Boolean value based on some criterion. Suppose, for example, that you only want to extract from a sequence of integers those numbers that are less than or equal to 15. A version of copy( ) called remove_copy_if( ) can do the job, like this:
//: C06:CopyInts2.cpp
// Ignores ints that satisfy a predicate.
#include <algorithm>
#include <cstddef>
#include <iostream>
using namespace std;
// You supply this predicate
bool gt15(int x) { return 15 < x; }
int main() {
int a[] = { 10, 20, 30 };
const size_t SIZE = sizeof a / sizeof a[0];
int b[SIZE];
int* endb = remove_copy_if(a, a+SIZE, b, gt15);
int* beginb = b;
while(beginb != endb)
cout << *beginb++ << endl; // Prints 10
only
} ///:~The remove_copy_if( ) function template takes the usual range-delimiting pointers, followed by a predicate of your choosing. The predicate must be a pointer to a function(86) that takes a single argument of the same type as the elements in the sequence, and it must return a bool. Here, the function gt15 returns true if its argument is greater than 15. The remove_copy_if( ) algorithm applies gt15( ) to each element in the input sequence and ignores those elements where the predicate yields true when writing to the output sequence.
The following program illustrates yet another variation of the copy algorithm:
//: C06:CopyStrings2.cpp
// Replaces strings that satisfy a predicate.
#include <algorithm>
#include <cstddef>
#include <iostream>
#include <string>
using namespace std;
// The predicate
bool contains_e(const string& s) {
return s.find('e') != string::npos;
}
int main() {
string a[] = {"read", "my",
"lips"};
const size_t SIZE = sizeof a / sizeof a[0];
string b[SIZE];
string* endb = replace_copy_if(a, a + SIZE, b,
contains_e, string("kiss"));
string* beginb = b;
while(beginb != endb)
cout << *beginb++ << endl;
} ///:~Instead of just ignoring elements that don't satisfy the predicate, replace_copy_if( ) substitutes a fixed value for such elements when populating the output sequence. The output is:
kiss
my
lipsbecause the original occurrence of “read,” the only input string containing the letter e, is replaced by the word “kiss,” as specified in the last argument in the call to replace_copy_if( ).
The replace_if( ) algorithm changes the original sequence in place, instead of writing to a separate output sequence, as the following program shows:
//: C06:ReplaceStrings.cpp
// Replaces strings in-place.
#include <algorithm>
#include <cstddef>
#include <iostream>
#include <string>
using namespace std;
bool contains_e(const string& s) {
return s.find('e') != string::npos;
}
int main() {
string a[] = {"read", "my",
"lips"};
const size_t SIZE = sizeof a / sizeof a[0];
replace_if(a, a + SIZE, contains_e,
string("kiss"));
string* p = a;
while(p != a + SIZE)
cout << *p++ << endl;
} ///:~2-4-1-2. Stream iterators▲
Like any good software library, the Standard C++ Library attempts to provide convenient ways to automate common tasks. We mentioned in the beginning of this chapter that you can use generic algorithms in place of looping constructs. So far, however, our examples have still used an explicit loop to print their output. Since printing output is one of the most common tasks, you would hope for a way to automate that too.
That's where stream iterators come in. A stream iterator uses a stream as either an input or an output sequence. To eliminate the output loop in the CopyInts2.cpp program, for instance, you can do something like the following:
//: C06:CopyInts3.cpp
// Uses an output stream iterator.
#include <algorithm>
#include <cstddef>
#include <iostream>
#include <iterator>
using namespace std;
bool gt15(int x) { return 15 < x; }
int main() {
int a[] = { 10, 20, 30 };
const size_t SIZE = sizeof a / sizeof a[0];
remove_copy_if(a, a + SIZE,
ostream_iterator<int>(cout,
"\n"), gt15);
} ///:~In this example we've replaced the output sequence b in the third argument of remove_copy_if( ) with an output stream iterator, which is an instance of the ostream_iterator class template declared in the <iterator> header. Output stream iterators overload their copy-assignment operators to write to their stream. This particular instance of ostream_iterator is attached to the output stream cout. Every time remove_copy_if( ) assigns an integer from the sequence a to cout through this iterator, the iterator writes the integer to cout and also automatically writes an instance of the separator string found in its second argument, which in this case contains the newline character.
It is just as easy to write to a file by providing an output file stream, instead of cout:
//: C06:CopyIntsToFile.cpp
// Uses an output file stream iterator.
#include <algorithm>
#include <cstddef>
#include <fstream>
#include <iterator>
using namespace std;
bool gt15(int x) { return 15 < x; }
int main() {
int a[] = { 10, 20, 30 };
const size_t SIZE = sizeof a / sizeof a[0];
ofstream outf("ints.out");
remove_copy_if(a, a + SIZE,
ostream_iterator<int>(outf,
"\n"), gt15);
} ///:~An input stream iterator allows an algorithm to get its input sequence from an input stream. This is accomplished by having both the constructor and operator++( ) read the next element from the underlying stream and by overloading operator*( ) to yield the value previously read. Since algorithms require two pointers to delimit an input sequence, you can construct an istream_iteratorin two ways, as you can see in the program that follows.
//: C06:CopyIntsFromFile.cpp
// Uses an input stream iterator.
#include <algorithm>
#include <fstream>
#include <iostream>
#include <iterator>
#include "../require.h"
using namespace std;
bool gt15(int x) { return 15 < x; }
int main() {
ofstream ints("someInts.dat");
ints << "1 3 47 5 84 9";
ints.close();
ifstream inf("someInts.dat");
assure(inf, "someInts.dat");
remove_copy_if(istream_iterator<int>(inf),
istream_iterator<int>(),
ostream_iterator<int>(cout,
"\n"), gt15);
} ///:~The first argument to replace_copy_if( ) in this program attaches an istream_iterator object to the input file stream containing ints. The second argument uses the default constructor of the istream_iterator class. This call constructs a special value of istream_iterator that indicates end-of-file, so that when the first iterator finally encounters the end of the physical file, it compares equal to the value istream_iterator<int>( ), allowing the algorithm to terminate correctly. Note that this example avoids using an explicit array altogether.
2-4-1-3. Algorithm complexity▲
Using a software library is a matter of trust. You trust the implementers to not only provide correct functionality, but you also hope that the functions execute as efficiently as possible. It's better to write your own loops than to use algorithms that degrade performance.
To guarantee quality library implementations, the C++ Standard not only specifies what an algorithm should do, but how fast it should do it and sometimes how much space it should use. Any algorithm that does not meet the performance requirements does not conform to the standard. The measure of an algorithm's operational efficiency is called its complexity.
When possible, the standard specifies the exact number of operation counts an algorithm should use. The count_if( ) algorithm, for example, returns the number of elements in a sequence satisfying a given predicate. The following call to count_if( ), if applied to a sequence of integers similar to the examples earlier in this chapter, yields the number of integer elements that are greater than 15:
size_t n = count_if(a, a + SIZE, gt15);Since count_if( ) must look at every element exactly once, it is specified to make a number of comparisons exactly equal to the number of elements in the sequence. The copy( ) algorithm has the same specification.
Other algorithms can be specified to take at most a certain number of operations. The find( ) algorithm searches through a sequence in order until it encounters an element equal to its third argument:
int* p = find(a, a + SIZE, 20);It stops as soon as the element is found and returns a pointer to that first occurrence. If it doesn't find one, it returns a pointer one position past the end of the sequence (a+SIZE in this example). So find() makes at most a number of comparisons equal to the number of elements in the sequence.
Sometimes the number of operations an algorithm takes cannot be measured with such precision. In such cases, the standard specifies the algorithm's asymptotic complexity, which is a measure of how the algorithm behaves with large sequences compared to well-known formulas. A good example is the sort( ) algorithm, which the standard says takes “approximately n log n comparisons on average” (n is the number of elements in the sequence).(87) Such complexity measures give a “feel” for the cost of an algorithm and at least give a meaningful basis for comparing algorithms. As you'll see in the next chapter, the find( ) member function for the set container has logarithmic complexity, which means that the cost of searching for an element in a set will, for large sets, be proportional to the logarithm of the number of elements. This is much smaller than the number of elements for large n, so it is always better to search a set by using its find( ) member function rather than by using the generic find( ) algorithm.
2-4-2. Function objects▲
As you study some of the examples earlier in this chapter, you will probably notice the limited utility of the function gt15( ). What if you want to use a number other than 15 as a comparison threshold? You may need a gt20( ) or gt25( ) or others as well. Having to write a separate function is time consuming, but also unreasonable because you must know all required values when you write your application code.
The latter limitation means that you can't use runtime values(88) to govern your searches, which is unacceptable. Overcoming this difficulty requires a way to pass information to predicates at runtime. For example, you would need a greater-than function that you can initialize with an arbitrary comparison value. Unfortunately, you can't pass that value as a function parameter because unary predicates, such as our gt15( ), are applied to each value in a sequence individually and must therefore take only one parameter.
The way out of this dilemma is, as always, to create an abstraction. Here, we need an abstraction that can act like a function as well as store state, without disturbing the number of function parameters it accepts when used. This abstraction is called a function object.(89)
A function object is an instance of a class that overloads operator( ), the function call operator. This operator allows an object to be used with function call syntax. As with any other object, you can initialize it via its constructors. Here is a function object that can be used in place of gt15( ):
//: C06:GreaterThanN.cpp
#include <iostream>
using namespace std;
class gt_n {
int value;
public:
gt_n(int val) : value(val) {}
bool operator()(int n) { return n > value; }
};
int main() {
gt_n f(4);
cout << f(3) << endl; // Prints 0 (for
false)
cout << f(5) << endl; // Prints 1 (for
true)
} ///:~The fixed value to compare against (4) is passed when the function object f is created. The expression f(3) is then evaluated by the compiler as the following function call:
f.operator()(3);which returns the value of the expression 3 > value, which is false when value is 4, as it is in this example.
Since such comparisons apply to types other than int, it would make sense to define gt_n( ) as a class template. It turns out you don't need to do it yourself, though—the standard library has already done it for you. The following descriptions of function objects should not only make that topic clear, but also give you a better understanding of how the generic algorithms work.
2-4-2-1. Classification of function objects▲
The Standard C++ library classifies a function object based on the number of arguments its operator( ) takes and the kind of value it returns. This classification is based on whether a function object's operator( ) takes zero, one, or two arguments:
Generator: A type of function object that takes no arguments and returns a value of an arbitrary type. A random number generator is an example of a generator. The standard library provides one generator, the function rand( ) declared in <cstdlib>, and has some algorithms, such as generate_n( ), which apply generators to a sequence.
Unary Function: A type of function object that takes a single argument of any type and returns a value that may be of a different type (which may be void).
Binary Function: A type of function object that takes two arguments of any two (possibly distinct) types and returns a value of any type (including void).
Unary Predicate: A Unary Function that returns a bool.
Binary Predicate: A Binary Function that returns a bool.
Strict Weak Ordering: A binary predicate that allows for a more general interpretation of “equality.” Some of the standard containers consider two elements equivalent if neither is less than the other (using operator<( )). This is important when comparing floating-point values, and objects of other types where operator==( ) is unreliable or unavailable. This notion also applies if you want to sort a sequence of data records (structs) on a subset of the struct's fields. That comparison scheme is considered a strict weak ordering because two records with equal keys are not really “equal” as total objects, but they are equal as far as the comparison you're using is concerned. The importance of this concept will become clearer in the next chapter.
In addition, certain algorithms make assumptions about the operations available for the types of objects they process. We will use the following terms to indicate these assumptions:
LessThanComparable: A class that has a less-than operator<.
Assignable: A class that has a copy-assignment operator= for its own type.
EqualityComparable: A class that has an equivalence operator== for its own type.
We will use these terms later in this chapter to describe the generic algorithms in the standard library.
2-4-2-2. Automatic creation of function objects▲
The <functional> header defines a number of useful generic function objects. They are admittedly simple, but you can use them to compose more complicated function objects. Consequently, in many instances, you can construct complicated predicates without writing a single function. You do so by using function object adaptors(90) to take the simple function objects and adapt them for use with other function objects in a chain of operations.
To illustrate, let's use only standard function objects to accomplish what gt15( ) did earlier. The standard function object, greater, is a binary function object that returns true if its first argument is greater than its second argument. We cannot apply this directly to a sequence of integers through an algorithm such as remove_copy_if( ) because remove_copy_if( ) expects a unary predicate. We can construct a unary predicate on the fly that uses greater to compare its first argument to a fixed value. We fix the value of the second parameter at 15 using the function object adaptor bind2nd, like this:
//: C06:CopyInts4.cpp
// Uses a standard function object and adaptor.
#include <algorithm>
#include <cstddef>
#include <functional>
#include <iostream>
#include <iterator>
using namespace std;
int main() {
int a[] = { 10, 20, 30 };
const size_t SIZE = sizeof a / sizeof a[0];
remove_copy_if(a, a + SIZE,
ostream_iterator<int>(cout,
"\n"),
bind2nd(greater<int>(), 15));
} ///:~This program produces the same result as CopyInts3.cpp, but without writing our own predicate function gt15( ). The function object adaptor bind2nd( ) is a template function that creates a function object of type binder2nd, which simply stores the two arguments passed to bind2nd( ), the first of which must be a binary function or function object (that is, anything that can be called with two arguments). The operator( ) function in binder2nd, which is itself a unary function, calls the binary function it stored, passing it its incoming parameter and the fixed value it stored.
To make the explanation concrete for this example, let's call the instance of binder2nd created by bind2nd( ) by the name b. When b is created, it receives two parameters (greater<int>( ) and 15) and stores them. Let's call the instance of greater<int> by the name g, and call the instance of the output stream iterator by the name o. Then the call to remove_copy_if( ) earlier conceptually becomes the following:
remove_copy_if(a, a + SIZE, o, b(g, 15).operator());As remove_copy_if( ) iterates through the sequence, it calls b on each element, to determine whether to ignore the element when copying to the destination. If we denote the current element by the name e, that call inside remove_copy_if( ) is equivalent to
if(b(e))but binder2nd's function call operator just turns around and calls g(e,15), so the earlier call is the same as
if(greater<int>(e, 15))which is the comparison we were seeking. There is also a bind1st( ) adaptor that creates a binder1st object, which fixes the first argument of the associated input binary function.
As another example, let's count the number of elements in the sequence not equal to 20. This time we'll use the algorithm count_if( ), introduced earlier. There is a standard binary function object, equal_to, and also a function object adaptor, not1( ), that takes a unary function object as a parameter and invert its truth value. The following program will do the job:
//: C06:CountNotEqual.cpp
// Count elements not equal to 20.
#include <algorithm>
#include <cstddef>
#include <functional>
#include <iostream>
using namespace std;
int main() {
int a[] = { 10, 20, 30 };
const size_t SIZE = sizeof a / sizeof a[0];
cout << count_if(a, a + SIZE,
not1(bind1st(equal_to<int>(),
20)));// 2
} ///:~As remove_copy_if( ) did in the previous example, count_if( ) calls the predicate in its third argument (let's call it n) for each element of its sequence and increments its internal counter each time true is returned. If, as before, we call the current element of the sequence by the name e, the statement
if(n(e))in the implementation of count_if is interpreted as
if(!bind1st(equal_to<int>, 20)(e))which ends up as
if(!equal_to<int>(20, e))because not1( ) returns the logical negation of the result of calling its unary function argument. The first argument to equal_to is 20 because we used bind1st( ) instead of bind2nd( ). Since testing for equality is symmetric in its arguments, we could have used either bind1st( ) or bind2nd( ) in this example.
The following table shows the templates that generate the standard function objects, along with the kinds of expressions to which they apply:
| Name | Type | Result produced |
|---|---|---|
| plus | BinaryFunction | arg1 + arg2 |
| minus | BinaryFunction | arg1 - arg2 |
| multiplies | BinaryFunction | arg1 * arg2 |
| divides | BinaryFunction | arg1 / arg2 |
| modulus | BinaryFunction | arg1 % arg2 |
| negate | UnaryFunction | - arg1 |
| equal_to | BinaryPredicate | arg1 == arg2 |
| not_equal_to | BinaryPredicate | arg1 != arg2 |
| greater | BinaryPredicate | arg1 > arg2 |
| less | BinaryPredicate | arg1 < arg2 |
| greater_equal | BinaryPredicate | arg1 >= arg2 |
| less_equal | BinaryPredicate | arg1 <= arg2 |
| logical_and | BinaryPredicate | arg1 && arg2 |
| Logical_or | BinaryPredicate | arg1 || arg2 |
| logical_not | UnaryPredicate | !arg1 |
| unary_negate | Unary Logical | !(UnaryPredicate(arg1)) |
| binary_negate | Binary Logical | !(BinaryPredicate(arg1, arg2)) |
2-4-2-3. Adaptable function objects▲
Standard function adaptors such as bind1st( ) and bind2nd( ) make some assumptions about the function objects they process. Consider the following expression from the last line of the earlier CountNotEqual.cpp program:
not1(bind1st(equal_to<int>(), 20))The bind1st( ) adaptor creates a unary function object of type binder1st, which simply stores an instance of equal_to<int> and the value 20. The binder1st::operator( ) function needs to know its argument type and its return type; otherwise, it will not have a valid declaration. The convention to solve this problem is to expect all function objects to provide nested type definitions for these types. For unary functions, the type names are argument_type and result_type; for binary function objects they are first_argument_type, second_argument_type, and result_type. Looking at the implementation of bind1st( ) and binder1st in the <functional> header reveals these expectations. First inspect bind1st( ), as it might appear in a typical library implementation:
template<class Op, class T>
binder1st<Op> bind1st(const Op& f, const
T& val) {
typedef typename Op::first_argument_type Arg1_t;
return binder1st<Op>(f, Arg1_t(val));
}Note that the template parameter, Op, which represents the type of the binary function being adapted by bind1st( ), must have a nested type named first_argument_type. (Note also the use of typename to inform the compiler that it is a member type name, as explained in Chapter 5.) Now see how binder1st uses the type names in Op in its declaration of its function call operator:
// Inside the implementation for binder1st<Op>
typename Op::result_type
operator()(const typename Op::second_argument_type&
x)
const;Function objects whose classes provide these type names are called adaptable function objects.
Since these names are expected of all standard function objects as well as of any function objects you create to use with function object adaptors, the <functional> header provides two templates that define these types for you: unary_function and binary_function. You simply derive from these classes while filling in the argument types as template parameters. Suppose, for example, that we want to make the function object gt_n, defined earlier in this chapter, adaptable. All we need to do is the following:
class gt_n : public unary_function<int, bool> {
int value;
public:
gt_n(int val) : value(val) {}
bool operator()(int n) {
return n > value;
}
};All unary_function does is to provide the appropriate type definitions, which it infers from its template parameters as you can see in its definition:
template<class Arg, class Result> struct
unary_function {
typedef Arg argument_type;
typedef Result result_type;
};These types become accessible through gt_n because it derives publicly from unary_function. The binary_function template behaves in a similar manner.
2-4-2-4. More function object examples▲
The following FunctionObjects.cpp example provides simple tests for most of the built-in basic function object templates. This way, you can see how to use each template, along with the resulting behavior. This example uses one of the following generators for convenience:
//: C06:Generators.h
// Different ways to fill sequences.
#ifndef GENERATORS_H
#define GENERATORS_H
#include <cstring>
#include <set>
#include <cstdlib>
// A generator that can skip over numbers:
class SkipGen {
int i;
int skp;
public:
SkipGen(int start = 0, int skip = 1)
: i(start), skp(skip) {}
int operator()() {
int r = i;
i += skp;
return r;
}
};
// Generate unique random numbers from 0 to mod:
class URandGen {
std::set<int> used;
int limit;
public:
URandGen(int lim) : limit(lim) {}
int operator()() {
while(true) {
int i = int(std::rand()) % limit;
if(used.find(i) == used.end()) {
used.insert(i);
return i;
}
}
}
};
// Produces random characters:
class CharGen {
static const char* source;
static const int len;
public:
char operator()() {
return source[std::rand() % len];
}
};
#endif // GENERATORS_H ///:~//: C06:Generators.cpp {O}
#include "Generators.h"
const char* CharGen::source = "ABCDEFGHIJK"
"LMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz";
const int CharGen::len = std::strlen(source);
///:~We'll be using these generating functions in various examples throughout this chapter. The SkipGen function object returns the next number of an arithmetic sequence whose common difference is held in its skp data member. A URandGen object generates a unique random number in a specified range. (It uses a set container, which we'll discuss in the next chapter.) A CharGen object returns a random alphabetic character. Here is a sample program using UrandGen:
//: C06:FunctionObjects.cpp {-bor}
// Illustrates selected predefined function object
// templates from the Standard C++ library.
//{L} Generators
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <functional>
#include <iostream>
#include <iterator>
#include <vector>
#include "Generators.h"
#include "PrintSequence.h"
using namespace std;
template<typename Contain, typename UnaryFunc>
void testUnary(Contain& source, Contain& dest,
UnaryFunc f) {
transform(source.begin(), source.end(), dest.begin(),
f);
}
template<typename Contain1, typename Contain2,
typename BinaryFunc>
void testBinary(Contain1& src1, Contain1& src2,
Contain2& dest, BinaryFunc f) {
transform(src1.begin(), src1.end(),
src2.begin(), dest.begin(), f);
}
// Executes the expression, then stringizes the
// expression into the print statement:
#define T(EXPR) EXPR; print(r.begin(), r.end(), \
"After " #EXPR);
// For Boolean tests:
#define B(EXPR) EXPR; print(br.begin(), br.end(), \
"After " #EXPR);
// Boolean random generator:
struct BRand {
bool operator()() { return rand() % 2 == 0; }
};
int main() {
const int SZ = 10;
const int MAX = 50;
vector<int> x(SZ), y(SZ), r(SZ);
// An integer random number generator:
URandGen urg(MAX);
srand(time(0)); // Randomize
generate_n(x.begin(), SZ, urg);
generate_n(y.begin(), SZ, urg);
// Add one to each to guarantee nonzero divide:
transform(y.begin(), y.end(), y.begin(),
bind2nd(plus<int>(), 1));
// Guarantee one pair of elements is ==:
x[0] = y[0];
print(x.begin(), x.end(), "x");
print(y.begin(), y.end(), "y");
// Operate on each element pair of x & y,
// putting the result into r:
T(testBinary(x, y, r, plus<int>()));
T(testBinary(x, y, r, minus<int>()));
T(testBinary(x, y, r, multiplies<int>()));
T(testBinary(x, y, r, divides<int>()));
T(testBinary(x, y, r, modulus<int>()));
T(testUnary(x, r, negate<int>()));
vector<bool> br(SZ); // For Boolean results
B(testBinary(x, y, br, equal_to<int>()));
B(testBinary(x, y, br, not_equal_to<int>()));
B(testBinary(x, y, br, greater<int>()));
B(testBinary(x, y, br, less<int>()));
B(testBinary(x, y, br, greater_equal<int>()));
B(testBinary(x, y, br, less_equal<int>()));
B(testBinary(x, y, br,
not2(greater_equal<int>())));
B(testBinary(x,y,br,not2(less_equal<int>())));
vector<bool> b1(SZ), b2(SZ);
generate_n(b1.begin(), SZ, BRand());
generate_n(b2.begin(), SZ, BRand());
print(b1.begin(), b1.end(), "b1");
print(b2.begin(), b2.end(), "b2");
B(testBinary(b1, b2, br, logical_and<int>()));
B(testBinary(b1, b2, br, logical_or<int>()));
B(testUnary(b1, br, logical_not<int>()));
B(testUnary(b1, br, not1(logical_not<int>())));
} ///:~This example uses a handy function template, print( ), which is capable of printing a sequence of any type along with an optional message. This template appears in the header file PrintSequence.h, and is explained later in this chapter.
The two template functions automate the process of testing the various function object templates. There are two because the function objects are either unary or binary. The testUnary( ) function takes a source vector, a destination vector, and a unary function object to apply to the source vector to produce the destination vector. In testBinary( ), two source vectors are fed to a binary function to produce the destination vector. In both cases, the template functions simply turn around and call the transform( ) algorithm, which applies the unary function or function object found in its fourth parameter to each sequence element, writing the result to the sequence indicated by its third parameter, which in this case is the same as the input sequence.
For each test, you want to see a string describing the test, followed by the results of the test. To automate this, the preprocessor comes in handy; the T( ) and B( ) macros each take the expression you want to execute. After evaluating the expression, they pass the appropriate range to print( ). To produce the message the expression is “stringized” using the preprocessor. That way you see the code of the expression that is executed followed by the result vector.
The last little tool, BRand, is a generator object that creates random bool values. To do this, it gets a random number from rand( ) and tests to see if it's greater than (RAND_MAX+1)/2. If the random numbers are evenly distributed, this should happen half the time.
In main( ), three vectors of int are created: x and y for source values, and r for results. To initialize x and y with random values no greater than 50, a generator of type URandGen from Generators.h is used. The standard generate_n( ) algorithm populates the sequence specified in its first argument by invoking its third argument (which must be a generator) a given number of times (specified in its second argument). Since there is one operation where elements of x are divided by elements of y, we must ensure that there are no zero values of y. This is accomplished by once again using the transform( ) algorithm, taking the source values from y and putting the results back into y. The function object for this is created with the expression:
bind2nd(plus<int>(), 1)This expression uses the plus function object to add 1 to its first argument. As we did earlier in this chapter, we use a binder adaptor to make this a unary function so it can applied to the sequence by a single call to transform( ).
Another test in the program compares the elements in the two vectors for equality, so it is interesting to guarantee that at least one pair of elements is equivalent; here element zero is chosen.
Once the two vectors are printed, T( ) tests each of the function objects that produces a numeric value, and then B( ) tests each function object that produces a Boolean result. The result is placed into a vector<bool>, and when this vector is printed, it produces a ‘1' for a true value and a ‘0' for a false value. Here is the output from an execution of FunctionObjects.cpp:
x:
4 8 18 36 22 6 29 19 25 47
y:
4 14 23 9 11 32 13 15 44 30
After testBinary(x, y, r, plus<int>()):
8 22 41 45 33 38 42 34 69 77
After testBinary(x, y, r, minus<int>()):
0 -6 -5 27 11 -26 16 4 -19 17
After testBinary(x, y, r, multiplies<int>()):
16 112 414 324 242 192 377 285 1100 1410
After testBinary(x, y, r, divides<int>()):
1 0 0 4 2 0 2 1 0 1
After testBinary(x, y, r, limit<int>()):
0 8 18 0 0 6 3 4 25 17
After testUnary(x, r, negate<int>()):
-4 -8 -18 -36 -22 -6 -29 -19 -25 -47
After testBinary(x, y, br, equal_to<int>()):
1 0 0 0 0 0 0 0 0 0
After testBinary(x, y, br, not_equal_to<int>()):
0 1 1 1 1 1 1 1 1 1
After testBinary(x, y, br, greater<int>()):
0 0 0 1 1 0 1 1 0 1
After testBinary(x, y, br, less<int>()):
0 1 1 0 0 1 0 0 1 0
After testBinary(x, y, br, greater_equal<int>()):
1 0 0 1 1 0 1 1 0 1
After testBinary(x, y, br, less_equal<int>()):
1 1 1 0 0 1 0 0 1 0
After testBinary(x, y, br,
not2(greater_equal<int>())):
0 1 1 0 0 1 0 0 1 0
After testBinary(x,y,br,not2(less_equal<int>())):
0 0 0 1 1 0 1 1 0 1
b1:
0 1 1 0 0 0 1 0 1 1
b2:
0 1 1 0 0 0 1 0 1 1
After testBinary(b1, b2, br, logical_and<int>()):
0 1 1 0 0 0 1 0 1 1
After testBinary(b1, b2, br, logical_or<int>()):
0 1 1 0 0 0 1 0 1 1
After testUnary(b1, br, logical_not<int>()):
1 0 0 1 1 1 0 1 0 0
After testUnary(b1, br,
not1(logical_not<int>())):
0 1 1 0 0 0 1 0 1 1If you want the Boolean values to display as “true” and “false” instead of 1 and 0, call cout.setf(ios::boolalpha).
A binder doesn't have to produce a unary predicate; it can also create any unary function (that is, a function that returns something other than bool). For example, you can to multiply every element in a vector by 10 using a binder with the transform( ) algorithm:
//: C06:FBinder.cpp
// Binders aren't limited to producing predicates.
//{L} Generators
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <functional>
#include <iostream>
#include <iterator>
#include <vector>
#include "Generators.h"
using namespace std;
int main() {
ostream_iterator<int> out(cout," ");
vector<int> v(15);
srand(time(0)); // Randomize
generate(v.begin(), v.end(), URandGen(20));
copy(v.begin(), v.end(), out);
transform(v.begin(), v.end(),
v.begin(),
bind2nd(multiplies<int>(), 10));
copy(v.begin(), v.end(), out);
} ///:~Since the third argument to transform( ) is the same as the first, the resulting elements are copied back into the source vector. The function object created by bind2nd( ) in this case produces an int result.
The “bound” argument to a binder cannot be a function object, but it does not have to be a compile-time constant. For example:
//: C06:BinderValue.cpp
// The bound argument can vary.
#include <algorithm>
#include <functional>
#include <iostream>
#include <iterator>
#include <cstdlib>
using namespace std;
int boundedRand() { return rand() % 100; }
int main() {
const int SZ = 20;
int a[SZ], b[SZ] = {0};
generate(a, a + SZ, boundedRand);
int val = boundedRand();
int* end = remove_copy_if(a, a + SZ, b,
bind2nd(greater<int>(), val));
// Sort for easier viewing:
sort(a, a + SZ);
sort(b, end);
ostream_iterator<int> out(cout, " ");
cout << "Original Sequence:” << endl;
copy(a, a + SZ, out); cout << endl;
cout << "Values <= " << val
<< endl;
copy(b, end, out); cout << endl;
} ///:~Here, an array is filled with 20 random numbers between 0 and 100, and the user provides a value on the command line. In the remove_copy_if( ) call, you can see that the bound argument to bind2nd( ) is random number in the same range as the sequence. Here is the output from one run:
Original Sequence:
4 12 15 17 19 21 26 30 47 48 56 58 60 63 71 79 82 90 92
95
Values <= 41
4 12 15 17 19 21 26 302-4-2-5. Function pointer adaptors▲
Wherever a function-like entity is expected by an algorithm, you can supply either a pointer to an ordinary function or a function object. When the algorithm issues a call, if it is through a function pointer, than the native function-call mechanism is used. If it is through a function object, then that object's operator( ) member executes. In CopyInts2.cpp, we passed the raw function gt15( ) as a predicate to remove_copy_if( ). We also passed pointers to functions returning random numbers to generate( ) and generate_n( ).
You cannot use raw functions with function object adaptors such as bind2nd( ) because they assume the existence of type definitions for the argument and result types. Instead of manually converting your native functions into function objects yourself, the standard library provides a family of adaptors to do the work for you. The ptr_fun( ) adaptors take a pointer to a function and turn it into a function object. They are not designed for a function that takes no arguments—they must only be used with unary functions or binary functions.
The following program uses ptr_fun( ) to wrap a unary function:
//: C06:PtrFun1.cpp
// Using ptr_fun() with a unary function.
#include <algorithm>
#include <cmath>
#include <functional>
#include <iostream>
#include <iterator>
#include <vector>
using namespace std;
int d[] = { 123, 94, 10, 314, 315 };
const int DSZ = sizeof d / sizeof *d;
bool isEven(int x) { return x % 2 == 0; }
int main() {
vector<bool> vb;
transform(d, d + DSZ, back_inserter(vb),
not1(ptr_fun(isEven)));
copy(vb.begin(), vb.end(),
ostream_iterator<bool>(cout, " "));
cout << endl;
// Output: 1 0 0 0 1
} ///:~We can't simply pass isEven to not1, because not1 needs to know the actual argument type and return type its argument uses. The ptr_fun( ) adaptor deduces those types through template argument deduction. The definition of the unary version of ptr_fun( ) looks something like this:
template<class Arg, class Result>
pointer_to_unary_function<Arg, Result>
ptr_fun(Result (*fptr)(Arg)) {
return
pointer_to_unary_function<Arg, Result>(fptr);
}As you can see, this version of ptr_fun( ) deduces the argument and result types from fptr and uses them to initialize a pointer_to_unary_function object that stores fptr. The function call operator for pointer_to_unary_function just calls fptr, as you can see by the last line of its code:
template<class Arg, class Result>
class pointer_to_unary_function
: public unary_function<Arg, Result> {
Result (*fptr)(Arg); // Stores the f-ptr
public:
pointer_to_unary_function(Result (*x)(Arg)) : fptr(x)
{}
Result operator()(Arg x) const { return fptr(x); }
};Since pointer_to_unary_function derives from unary_function, the appropriate type definitions come along for the ride and are available to not1.
There is also a binary version of ptr_fun( ), which returns a pointer_to_binary_function object (which derives from binary_function) that behaves analogously to the unary case. The following program uses the binary version of ptr_fun( ) to raise numbers in a sequence to a power. It also reveals a pitfall when passing overloaded functions to ptr_fun( ).
//: C06:PtrFun2.cpp {-edg}
// Using ptr_fun() for a binary function.
#include <algorithm>
#include <cmath>
#include <functional>
#include <iostream>
#include <iterator>
#include <vector>
using namespace std;
double d[] = { 01.23, 91.370, 56.661,
023.230, 19.959, 1.0, 3.14159 };
const int DSZ = sizeof d / sizeof *d;
int main() {
vector<double> vd;
transform(d, d + DSZ, back_inserter(vd),
bind2nd(ptr_fun<double, double, double>(pow),
2.0));
copy(vd.begin(), vd.end(),
ostream_iterator<double>(cout, "
"));
cout << endl;
} ///:~The pow( ) function is overloaded in the Standard C++ header <cmath> for each of the floating-point data types, as follows:
float pow(float, int); // Efficient int power versions
...
double pow(double, int);
long double pow(long double, int);
float pow(float, float);
double pow(double, double);
long double pow(long double, long double);Since there are multiple versions of pow( ), the compiler has no way of knowing which to choose. Here, we have to help the compiler by using explicit function template specialization, as explained in the previous chapter.(91)
It's even trickier to convert a member function into a function object suitable for using with the generic algorithms. As a simple example, suppose we have the classical “shape” problem and want to apply the draw( ) member function to each pointer in a container of Shape:
//: C06:MemFun1.cpp
// Applying pointers to member functions.
#include <algorithm>
#include <functional>
#include <iostream>
#include <vector>
#include "../purge.h"
using namespace std;
class Shape {
public:
virtual void draw() = 0;
virtual ~Shape() {}
};
class Circle : public Shape {
public:
virtual void draw() { cout <<
"Circle::Draw()" << endl; }
~Circle() { cout <<
"Circle::~Circle()" << endl; }
};
class Square : public Shape {
public:
virtual void draw() { cout << "Square::Draw()"
<< endl; }
~Square() { cout <<
"Square::~Square()" << endl; }
};
int main() {
vector<Shape*> vs;
vs.push_back(new Circle);
vs.push_back(new Square);
for_each(vs.begin(), vs.end(),
mem_fun(&Shape::draw));
purge(vs);
} ///:~The for_each( ) algorithm passes each element in a sequence to the function object denoted by its third argument. Here, we want the function object to wrap one of the member functions of the class itself, and so the function object's “argument” becomes the pointer to the object for the member function call. To produce such a function object, the mem_fun( ) template takes a pointer to a member as its argument.
The mem_fun( ) functions are for producing function objects that are called using a pointer to the object that the member function is called for, while mem_fun_ref( ) calls the member function directly for an object. One set of overloads of both mem_fun( ) and mem_fun_ref( ) is for member functions that take zero arguments and one argument, and this is multiplied by two to handle const vs. non-const member functions. However, templates and overloading take care of sorting all that out—all you need to remember is when to use mem_fun( ) vs. mem_fun_ref( ).
Suppose you have a container of objects (not pointers), and you want to call a member function that takes an argument. The argument you pass should come from a second container of objects. To accomplish this, use the second overloaded form of the transform( ) algorithm:
//: C06:MemFun2.cpp
// Calling member functions through an object reference.
#include <algorithm>
#include <functional>
#include <iostream>
#include <iterator>
#include <vector>
using namespace std;
class Angle {
int degrees;
public:
Angle(int deg) : degrees(deg) {}
int mul(int times) { return degrees *= times; }
};
int main() {
vector<Angle> va;
for(int i = 0; i < 50; i += 10)
va.push_back(Angle(i));
int x[] = { 1, 2, 3, 4, 5 };
transform(va.begin(), va.end(), x,
ostream_iterator<int>(cout, " "),
mem_fun_ref(&Angle::mul));
cout << endl;
// Output: 0 20 60 120 200
} ///:~Because the container is holding objects, mem_fun_ref( ) must be used with the pointer-to-member function. This version of transform( ) takes the start and end point of the first range (where the objects live); the starting point of the second range, which holds the arguments to the member function; the destination iterator, which in this case is standard output; and the function object to call for each object. This function object is created with mem_fun_ref( ) and the desired pointer to member. Notice that the transform( ) and for_each( ) template functions are incomplete; transform( ) requires that the function it calls return a value, and there is no for_each( ) that passes two arguments to the function it calls. Thus, you cannot call a member function that returns void and takes an argument using transform( ) or for_each( ).
Most any member function works with mem_fun_ref( ). You can also use standard library member functions, if your compiler doesn't add any default arguments beyond the normal arguments specified in the standard.(92) For example, suppose you'd like to read a file and search for blank lines. Your compiler may allow you to use the string::empty( ) member function like this:
//: C06:FindBlanks.cpp
// Demonstrates mem_fun_ref() with string::empty().
#include <algorithm>
#include <cassert>
#include <cstddef>
#include <fstream>
#include <functional>
#include <string>
#include <vector>
#include "../require.h"
using namespace std;
typedef vector<string>::iterator LSI;
int main(int argc, char* argv[]) {
char* fname = "FindBlanks.cpp";
if(argc > 1) fname = argv[1];
ifstream in(fname);
assure(in, fname);
vector<string> vs;
string s;
while(getline(in, s))
vs.push_back(s);
vector<string> cpy = vs; // For testing
LSI lsi = find_if(vs.begin(), vs.end(),
mem_fun_ref(&string::empty));
while(lsi != vs.end()) {
*lsi = "A BLANK LINE";
lsi = find_if(vs.begin(), vs.end(),
mem_fun_ref(&string::empty));
}
for(size_t i = 0; i < cpy.size(); i++)
if(cpy[i].size() == 0)
assert(vs[i] == "A BLANK LINE");
else
assert(vs[i] != "A BLANK LINE");
} ///:~This example uses find_if( ) to locate the first blank line in the given range using mem_fun_ref( ) with string::empty( ). After the file is opened and read into the vector, the process is repeated to find every blank line in the file. Each time a blank line is found, it is replaced with the characters “A BLANK LINE.” All you have to do to accomplish this is dereference the iterator to select the current string.
2-4-2-6. Writing your own function object adaptors▲
Consider how to write a program that converts strings representing floating-point numbers to their actual numeric values. To get things started, here's a generator that creates the strings:
//: C06:NumStringGen.h
// A random number generator that produces
// strings representing floating-point numbers.
#ifndef NUMSTRINGGEN_H
#define NUMSTRINGGEN_H
#include <cstdlib>
#include <string>
class NumStringGen {
const int sz; // Number of digits to make
public:
NumStringGen(int ssz = 5) : sz(ssz) {}
std::string operator()() {
std::string digits("0123456789");
const int ndigits = digits.size();
std::string r(sz, ' ');
// Don't want a zero as the first digit
r[0] = digits[std::rand() % (ndigits - 1)] + 1;
// Now assign the rest
for(int i = 1; i < sz; ++i)
if(sz >= 3 && i
== sz/2)
r[i] = '.'; // Insert a decimal point
else
r[i] = digits[std::rand() % ndigits];
return r;
}
};
#endif // NUMSTRINGGEN_H ///:~You tell it how big the strings should be when you create the NumStringGen object. The random number generator selects digits, and a decimal point is placed in the middle.
The following program uses NumStringGen to fill a vector<string>. However, to use the standard C library function atof( ) to convert the strings to floating-point numbers, the string objects must first be turned into char pointers, since there is no automatic type conversion from string to char*. The transform( ) algorithm can be used with mem_fun_ref( ) and string::c_str( ) to convert all the strings to char*, and then these can be transformed using atof.
//: C06:MemFun3.cpp
// Using mem_fun().
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <functional>
#include <iostream>
#include <iterator>
#include <string>
#include <vector>
#include "NumStringGen.h"
using namespace std;
int main() {
const int SZ = 9;
vector<string> vs(SZ);
// Fill it with random number strings:
srand(time(0)); // Randomize
generate(vs.begin(), vs.end(), NumStringGen());
copy(vs.begin(), vs.end(),
ostream_iterator<string>(cout,
"\t"));
cout << endl;
const char* vcp[SZ];
transform(vs.begin(), vs.end(), vcp,
mem_fun_ref(&string::c_str));
vector<double> vd;
transform(vcp, vcp + SZ, back_inserter(vd),
std::atof);
cout.precision(4);
cout.setf(ios::showpoint);
copy(vd.begin(), vd.end(),
ostream_iterator<double>(cout,
"\t"));
cout << endl;
} ///:~This program does two transformations: one to convert strings to C-style strings (arrays of characters), and one to convert the C-style strings to numbers via atof( ). It would be nice to combine these two operations into one. After all, we can compose functions in mathematics, so why not C++?
The obvious approach takes the two functions as arguments and applies them in the proper order:
//: C06:ComposeTry.cpp
// A first attempt at implementing function composition.
#include <cassert>
#include <cstdlib>
#include <functional>
#include <iostream>
#include <string>
using namespace std;
template<typename R, typename E, typename F1,
typename F2>
class unary_composer {
F1 f1;
F2 f2;
public:
unary_composer(F1 fone, F2 ftwo) : f1(fone), f2(ftwo)
{}
R operator()(E x) { return f1(f2(x)); }
};
template<typename R, typename E, typename F1,
typename F2>
unary_composer<R, E, F1, F2> compose(F1 f1, F2
f2) {
return unary_composer<R, E, F1, F2>(f1, f2);
}
int main() {
double x = compose<double, const string&>(
atof,
mem_fun_ref(&string::c_str))("12.34");
assert(x == 12.34);
} ///:~The unary_composer object in this example stores the function pointers atof and string::c_str such that the latter function is applied first when its operator( ) is called. The compose( ) function adaptor is a convenience, so we don't need to supply all four template arguments explicitly—F1 and F2 are deduced from the call.
It would be much better if we didn't need to supply any template arguments. This is achieved by adhering to the convention for type definitions for adaptable function objects. In other words, we will assume that the functions to be composed are adaptable. This requires that we use ptr_fun( ) for atof( ). For maximum flexibility, we also make unary_composer adaptable in case it gets passed to a function adaptor. The following program does so and easily solves the original problem:
//: C06:ComposeFinal.cpp {-edg}
// An adaptable composer.
#include <algorithm>
#include <cassert>
#include <cstdlib>
#include <functional>
#include <iostream>
#include <iterator>
#include <string>
#include <vector>
#include "NumStringGen.h"
using namespace std;
template<typename F1, typename F2> class
unary_composer
: public unary_function<typename F2::argument_type,
typename F1::result_type> {
F1 f1;
F2 f2;
public:
unary_composer(F1 f1, F2 f2) : f1(f1), f2(f2) {}
typename F1::result_type
operator()(typename F2::argument_type x) {
return f1(f2(x));
}
};
template<typename F1, typename F2>
unary_composer<F1, F2> compose(F1 f1, F2 f2) {
return unary_composer<F1, F2>(f1, f2);
}
int main() {
const int SZ = 9;
vector<string> vs(SZ);
// Fill it with random number strings:
generate(vs.begin(), vs.end(), NumStringGen());
copy(vs.begin(), vs.end(),
ostream_iterator<string>(cout,
"\t"));
cout << endl;
vector<double> vd;
transform(vs.begin(), vs.end(), back_inserter(vd),
compose(ptr_fun(atof),
mem_fun_ref(&string::c_str)));
copy(vd.begin(), vd.end(),
ostream_iterator<double>(cout,
"\t"));
cout << endl;
} ///:~Once again we must use typename to let the compiler know that the member we are referring to is a nested type.
Some implementations(93) support composition of function objects as an extension, and the C++ Standards Committee is likely to add these capabilities to the next version of Standard C++.
2-4-3. A catalog of STL algorithms▲
This section provides a quick reference when you're searching for the appropriate algorithm. We leave the full exploration of all the STL algorithms to other references (see the end of this chapter, and Appendix A), along with the more intimate details of issues like performance. Our goal here is for you to rapidly become comfortable with the algorithms, and we'll assume you will look into the more specialized references if you need more detail.
Although you will often see the algorithms described using their full template declaration syntax, we're not doing that here because you already know they are templates, and it's quite easy to see what the template arguments are from the function declarations. The type names for the arguments provide descriptions for the types of iterators required. We think you'll find this form is easier to read, and you can quickly find the full declaration in the template header file if you need it.
The reason for all the fuss about iterators is to accommodate any type of container that meets the requirements in the standard library. So far we have illustrated the generic algorithms with only arrays and vectors as sequences, but in the next chapter you'll see a broad range of data structures that support less robust iteration. For this reason, the algorithms are categorized in part by the types of iteration facilities they require.
The names of the iterator classes describe the iterator type to which they must conform. There are no interface base classes to enforce these iteration operations—they are just expected to be there. If they are not, your compiler will complain. The various flavors of iterators are described briefly as follows.
InputIterator.An input iterator only allows reading elements of its sequence in a single, forward pass using operator++ and operator*. Input iteratorscan also be tested with operator== and operator!=. That's the extent of the constraints.
OutputIterator.An output iterator only allows writing elements to a sequence in a single, forward pass using operator++ and operator*. OutputIterators cannot be tested with operator== and operator!=, however, because you assume that you can just keep sending elements to the destination and that you don't need to see if the destination's end marker was reached. That is, the container that an OutputIterator references can take an infinite number of objects, so no end-checking is necessary. This requirement is important so that an OutputIterator can be used with ostreams (via ostream_iterator), but you'll also commonly use the “insert” iterators such as are the type of iterator returned by back_inserter( )).
There is no way to determine whether multiple InputIterators or OutputIterators point within the same range, so there is no way to use such iterators together. Just think in terms of iterators to support istreams and ostreams, and InputIterator and OutputIterator will make perfect sense. Also note that algorithms that use InputIterators or OutputIterators put the weakest restrictions on the types of iterators they will accept, which means that you can use any “more sophisticated” type of iterator when you see InputIterator or OutputIterator used as STL algorithm template arguments.
ForwardIterator. Because you can only read from an InputIterator and write to an OutputIterator, you can't use either of them to simultaneously read and modify a range, and you can't dereference such an iterator more than once. With a ForwardIterator these restrictions are relaxed; you can still only move forward using operator++, but you can both write and read, and you can compare such iterators in the same range for equality. Since forward iterators can both read and write, they can be used in place of an InputIterator or OutputIterator.
BidirectionalIterator.Effectively, this is a ForwardIterator that can also go backward. That is, a BidirectionalIterator supports all the operations that a ForwardIterator does, but in addition it has an operator--.
RandomAccessIterator. This type of iterator supports all the operations that a regular pointer does: you can add and subtract integral values to move it forward and backward by jumps (rather than just one element at a time), you can subscript it with operator[ ], you can subtract one iterator from another, and you can compare iterators to see which is greater using operator<, operator>, and so on. If you're implementing a sorting routine or something similar, random access iterators are necessary to be able to create an efficient algorithm.
The names used for the template parameter types in the algorithm descriptions later in this chapter consist of the listed iterator types (sometimes with a ‘1' or ‘2' appended to distinguish different template arguments) and can also include other arguments, often function objects.
When describing the group of elements passed to an operation, mathematical “range” notation is often used. In this, the square bracket means “includes the end point,” and the parenthesis means “does not include the end point.” When using iterators, a range is determined by the iterator pointing to the initial element and by the “past-the-end” iterator, pointing past the last element. Since the past-the-end element is never used, the range determined by a pair of iterators can be expressed as [first, last), where first is the iterator pointing to the initial element, and last is the past-the-end iterator.
Most books and discussions of the STL algorithms arrange them according to side-effects: non-mutating algorithms don't change the elements in the range, mutating algorithms do change the elements, and so on. These descriptions are based primarily on the underlying behavior or implementation of the algorithm—that is, on the designer's perspective. In practice, we don't find this a useful categorization, so instead we'll organize them according to the problem you want to solve: Are you searching for an element or set of elements, performing an operation on each element, counting elements, replacing elements, and so on? This should help you find the algorithm you want more easily.
If you do not see a different header such as <utility> or <numeric> above the function declarations, it appears in <algorithm>. Also, all the algorithms are in the namespace std.
2-4-3-1. Support tools for example creation▲
It's useful to create some basic tools to test the algorithms. In the examples that follow we'll use the generators mentioned earlier in Generators.h, as well as what appears below.
Displaying a range is a frequent task, so here is a function template to print any sequence, regardless of the type contained in that sequence:
//:
C06:PrintSequence.h
// Prints
the contents of any sequence.
#ifndef
PRINTSEQUENCE_H
#define
PRINTSEQUENCE_H
#include
<algorithm>
#include
<iostream>
#include
<iterator>
template<typename
Iter>
void
print(Iter first, Iter last, const char* nm = "",
const char* sep = "\n",
std::ostream& os = std::cout) {
if(nm != 0
&& *nm != '\0')
os
<< nm << ": " << sep;
typedef
typename
std::iterator_traits<Iter>::value_type T;
std::copy(first, last,
std::ostream_iterator<T>(std::cout, sep));
os
<< std::endl;
}
#endif //
PRINTSEQUENCE_H ///:~By default this function template prints to cout with newlines as separators, but you can change that by modifying the default argument. You can also provide a message to print at the head of the output. Since print( ) uses the copy( ) algorithm to send objects to cout via an ostream_iterator, the ostream_iterator must know the type of object it is printing, which we infer from the value_type member of the iterator passed.
The std::iterator_traits template enables the print( ) function template to process sequences delimited by any type of iterator. The iterator types returned by the standard containers such as vector define a nested type, value_type, which represents the element type, but when using arrays, the iterators are just pointers, which can have no nested types. To supply the conventional types associated with iterators in the standard library, std::iterator_traits provides the following partial specialization for pointer types:
template<class T>
struct iterator_traits<T*> {
typedef random_access_iterator_tag
iterator_category;
typedef T value_type;
typedef ptrdiff_t difference_type;
typedef T* pointer;
typedef T& reference;
};This makes the type of the elements pointed at (namely, T) available via the type name value_type.
Stable vs. unstable reordering
A number of the STL algorithms that move elements of a sequence around distinguish between stable and unstable reordering of a sequence. A stable sort preserves the original relative order of the elements that are equivalent as far as the comparison function is concerned. For example, consider a sequence { c(1), b(1), c(2), a(1), b(2), a(2) }. These elements are tested for equivalence based on their letters, but their numbers indicate how they first appeared in the sequence. If you sort (for example) this sequence using an unstable sort, there's no guarantee of any particular order among equivalent letters, so you could end up with { a(2), a(1), b(1), b(2), c(2), c(1) }. However, if you use a stable sort, you will get { a(1), a(2), b(1), b(2), c(1), c(2) }. The STL sort( ) algorithm uses a variation of quicksort and is thus unstable, but a stable_sort( ) is also provided.(94)
To demonstrate the stability versus instability of algorithms that reorder a sequence, we need some way to keep track of how the elements originally appeared. The following is a kind of string object that keeps track of the order in which that particular object originally appeared, using a static map that maps NStrings to Counters. Each NString then contains an occurrence field that indicates the order in which this NString was discovered.
//: C06:NString.h
// A "numbered string" that keeps track of
the
// number of occurrences of the word it contains.
#ifndef NSTRING_H
#define NSTRING_H
#include <algorithm>
#include <iostream>
#include <string>
#include <utility>
#include <vector>
typedef std::pair<std::string, int> psi;
// Only compare on the first element
bool operator==(const psi& l, const psi& r) {
return l.first == r.first;
}
class NString {
std::string s;
int thisOccurrence;
// Keep track of the number of occurrences:
typedef std::vector<psi> vp;
typedef vp::iterator vpit;
static vp words;
void addString(const std::string& x) {
psi p(x, 0);
vpit it = std::find(words.begin(), words.end(), p);
if(it != words.end())
thisOccurrence = ++it->second;
else {
thisOccurrence = 0;
words.push_back(p);
}
}
public:
NString() : thisOccurrence(0) {}
NString(const std::string& x) : s(x) {
addString(x); }
NString(const char* x) : s(x) { addString(x); }
// Implicit operator= and copy-constructor are OK
here.
friend std::ostream& operator<<(
std::ostream& os, const NString& ns) {
return os << ns.s << " ["
<< ns.thisOccurrence << "]";
}
// Need this for sorting. Notice it only
// compares strings, not occurrences:
friend bool
operator<(const NString& l, const NString&
r) {
return l.s < r.s;
}
friend
bool operator==(const NString& l, const
NString& r) {
return l.s == r.s;
}
// For sorting with greater<NString>:
friend bool
operator>(const NString& l, const NString&
r) {
return l.s > r.s;
}
// To get at the string directly:
operator const std::string&() const { return s; }
};
// Because NString::vp is a template and we are using
the
// inclusion model, it must be defined in this header
file:
NString::vp NString::words;
#endif // NSTRING_H ///:~We would normally use a map container to associate a string with its number of occurrences, but maps don't appear until the next chapter, so we use a vector of pairs instead. You'll see plenty of similar examples in Chapter 7.
The only operator necessary to perform an ordinary ascending sort is NString::operator<( ). To sort in reverse order, the operator>( ) is also provided so that the greater template can call it.
2-4-3-2. Filling and generating▲
These algorithms let you automatically fill a range with a particular value or generate a set of values for a particular range. The “fill” functions insert a single value multiple times into the container. The “generate” functions use generators such as those described earlier to produce values to insert into the container.
void fill(ForwardIterator
first, ForwardIterator last,
const T& value);
void fill_n(OutputIterator first, Size n, const T& value);
fill( ) assigns value to every element in the range [first, last). fill_n( ) assigns value to n elements starting at first.
void generate(ForwardIterator
first, ForwardIterator last,
Generator gen);
void generate_n(OutputIterator first, Size n, Generator
gen);
generate( ) makes a call to gen( ) for each element in the range [first, last), presumablyto produce a different value for each element. generate_n( ) calls gen( )n times and assigns each result to n elements starting at first.
Example
The following example fills and generates into vectors. It also shows the use of print( ):
//: C06:FillGenerateTest.cpp
// Demonstrates "fill" and "generate."
//{L} Generators
#include <vector>
#include <algorithm>
#include <string>
#include "Generators.h"
#include "PrintSequence.h"
using namespace std;
int main() {
vector<string> v1(5);
fill(v1.begin(), v1.end(), "howdy");
print(v1.begin(), v1.end(), "v1", "
");
vector<string> v2;
fill_n(back_inserter(v2), 7, "bye");
print(v2.begin(), v2.end(), "v2");
vector<int> v3(10);
generate(v3.begin(), v3.end(), SkipGen(4,5));
print(v3.begin(), v3.end(), "v3", "
");
vector<int> v4;
generate_n(back_inserter(v4),15, URandGen(30));
print(v4.begin(), v4.end(), "v4", "
");
} ///:~A vector<string> is created with a predefined size. Since storage has already been created for all the string objects in the vector, fill( ) can use its assignment operator to assign a copy of “howdy” to each space in the vector. Also, the default newline separator is replaced with a space.
The second vector<string> v2 is not given an initial size, so back_inserter( ) must be used to force new elements in instead of trying to assign to existing locations.
The generate( ) and generate_n( ) functions have the same form as the “fill” functions except that they use a generator instead of a constant value. Here, both generators are demonstrated.
2-4-3-3. Counting▲
All containers have a member function size( ) that tells you how many elements they hold. The return type of size( ) is the iterator's difference_type(95) (usually ptrdiff_t), which we denote by IntegralValue in the following. The following two algorithms count objects that satisfy certain criteria.
IntegralValue count(InputIterator
first, InputIterator
last, const EqualityComparable& value);
Produces the number of elements in [first, last) that are equivalent to value (when tested using operator==).
IntegralValue count_if(InputIterator
first, InputIterator
last, Predicate pred);
Produces the number of elementsin [first, last) that each cause pred to return true.
Example
Here, a vector<char> v isfilled with random characters (including some duplicates). A set<char> is initialized from v, so it holds only one of each letter represented in v. This set counts all the instances of all the characters, which are then displayed:
//: C06:Counting.cpp
// The counting algorithms.
//{L} Generators
#include <algorithm>
#include <functional>
#include <iterator>
#include <set>
#include <vector>
#include "Generators.h"
#include "PrintSequence.h"
using namespace std;
int main() {
vector<char> v;
generate_n(back_inserter(v), 50, CharGen());
print(v.begin(), v.end(), "v",
"");
// Create a set of the characters in v:
set<char> cs(v.begin(), v.end());
typedef set<char>::iterator sci;
for(sci it = cs.begin(); it != cs.end(); it++) {
int n = count(v.begin(), v.end(), *it);
cout << *it << ": " <<
n << ", ";
}
int lc = count_if(v.begin(), v.end(),
bind2nd(greater<char>(), 'a'));
cout << "\nLowercase letters: "
<< lc << endl;
sort(v.begin(), v.end());
print(v.begin(), v.end(), "sorted",
"");
} ///:~The count_if( ) algorithm is demonstrated by counting all the lowercase letters; the predicate is created using the bind2nd( ) and greater function object templates.
2-4-3-4. Manipulating sequences▲
These algorithms let you move sequences around.
OutputIterator copy(InputIterator first, InputIterator last, OutputIterator destination);
Using assignment, copies from [first, last) to destination, incrementing destination after each assignment. This is essentially a “shuffle-left” operation, and so the source sequence must not contain the destination. Because assignment is used, you cannot directly insert elements into an empty container or at the end of a container, but instead you must wrap the destination iterator in an insert_iterator (typically by using back_inserter( ) or by using inserter( ) in the case of an associative container).
BidirectionalIterator2 copy_backward(BidirectionalIterator1
first, BidirectionalIterator1 last,
BidirectionalIterator2 destinationEnd);
Like copy( ), but copies the elements in reverse order. This is essentially a “shuffle-right” operation, and, like copy( ), the source sequence must not contain the destination. The source range [first, last) is copied to the destination, but the first destination element is destinationEnd - 1. This iterator is then decremented after each assignment. The space in the destination range must already exist (to allow assignment), and the destination range cannot be within the source range.
void reverse(BidirectionalIterator
first,
BidirectionalIterator last);
OutputIterator reverse_copy(BidirectionalIterator first,
BidirectionalIterator last, OutputIterator destination);
Both forms of this function reverse the range [first, last). reverse( ) reverses the range in place, and reverse_copy( ) leaves the original range alone and copies the reversed elements into destination, returning the past-the-end iterator of the resulting range.
ForwardIterator2 swap_ranges(ForwardIterator1
first1,
ForwardIterator1 last1, ForwardIterator2 first2);
Exchanges the contents of two ranges of equal size by swapping corresponding elements.
void rotate(ForwardIterator
first, ForwardIterator middle,
ForwardIterator last);
OutputIterator rotate_copy(ForwardIterator first,
ForwardIterator middle, ForwardIterator last,
OutputIterator destination);
Moves the contents of [first, middle) to the end of the sequence, and the contents of [middle, last) to the beginning. With rotate( ), the swap is performed in place; and with rotate_copy( ) the original range is untouched, and the rotated version is copied into destination, returning the past-the-end iterator of the resulting range. Note that while swap_ranges( ) requires that the two ranges be exactly the same size, the “rotate” functions do not.
bool next_permutation(BidirectionalIterator
first,
BidirectionalIterator last);
bool next_permutation(BidirectionalIterator first,
BidirectionalIterator last, StrictWeakOrdering
binary_pred);
bool prev_permutation(BidirectionalIterator first,
BidirectionalIterator last);
bool prev_permutation(BidirectionalIterator first,
BidirectionalIterator last, StrictWeakOrdering
binary_pred);
A permutation is one unique ordering of a set of elements. If you have n unique elements, there are n! (n factorial) distinct possible combinations of those elements. All these combinations can be conceptually sorted into a sequence using a lexicographical (dictionary-like) ordering and thus produce a concept of a “next” and “previous” permutation. So whatever the current ordering of elements in the range, there is a distinct “next” and “previous” permutation in the sequence of permutations.
The next_permutation( ) and prev_permutation( ) functions rearrange the elements into their next or previous permutation and, if successful, return true. If there are no more “next” permutations, the elements are in sorted order so next_permutation( ) returns false. If there are no more “previous” permutations, the elements are in descending sorted order so previous_permutation( ) returns false.
The versions of the functions that have a StrictWeakOrdering argument perform the comparisons using binary_pred instead of operator<.
void random_shuffle(RandomAccessIterator
first,
RandomAccessIterator last);
void random_shuffle(RandomAccessIterator first,
RandomAccessIterator last RandomNumberGenerator& rand);
This function randomly rearranges the elements in the range. It yields uniformly distributed results if the random-number generator does. The first form uses an internal random number generator, and the second uses a user-supplied random-number generator. The generator must return a value in the range [0, n) for some positive n.
BidirectionalIterator partition(BidirectionalIterator
first, BidirectionalIterator last, Predicate pred);
BidirectionalIterator stable_partition(BidirectionalIterator first,
BidirectionalIterator last, Predicate pred);
The “partition” functions move elements that satisfy pred to the beginning of the sequence. An iterator pointing one past the last of those elements is returned (which is, in effect, an “end” iterator” for the initial subsequence of elements that satisfy pred). This location is often called the “partition point.”
With partition( ), the order of the elements in each resulting subsequence after the function call is not specified, but with stable_partition( ), the relative order of the elements before and after the partition point will be the same as before the partitioning process.
Example
This gives a basic demonstration of sequence manipulation:
//: C06:Manipulations.cpp
// Shows basic manipulations.
//{L} Generators
// NString
#include <vector>
#include <string>
#include <algorithm>
#include "PrintSequence.h"
#include "NString.h"
#include "Generators.h"
using namespace std;
int main() {
vector<int> v1(10);
// Simple counting:
generate(v1.begin(), v1.end(), SkipGen());
print(v1.begin(), v1.end(), "v1", "
");
vector<int> v2(v1.size());
copy_backward(v1.begin(), v1.end(), v2.end());
print(v2.begin(), v2.end(),
"copy_backward", " ");
reverse_copy(v1.begin(), v1.end(), v2.begin());
print(v2.begin(), v2.end(), "reverse_copy",
" ");
reverse(v1.begin(), v1.end());
print(v1.begin(), v1.end(), "reverse",
" ");
int half = v1.size() / 2;
// Ranges must be exactly the same size:
swap_ranges(v1.begin(), v1.begin() + half,
v1.begin() + half);
print(v1.begin(), v1.end(), "swap_ranges",
" ");
// Start with a fresh sequence:
generate(v1.begin(), v1.end(), SkipGen());
print(v1.begin(), v1.end(), "v1", "
");
int third = v1.size() / 3;
for(int i = 0; i < 10; i++) {
rotate(v1.begin(), v1.begin() + third, v1.end());
print(v1.begin(), v1.end(), "rotate",
" ");
}
cout << "Second rotate example:"
<< endl;
char c[] = "aabbccddeeffgghhiijj";
const char CSZ = strlen(c);
for(int i = 0; i < 10; i++) {
rotate(c, c + 2, c + CSZ);
print(c, c + CSZ, "", "");
}
cout << "All n! permutations of abcd:"
<< endl;
int nf = 4 * 3 * 2 * 1;
char p[] = "abcd";
for(int i = 0; i < nf; i++) {
next_permutation(p, p + 4);
print(p, p + 4, "", "");
}
cout << "Using prev_permutation:"
<< endl;
for(int i = 0; i < nf; i++) {
prev_permutation(p, p + 4);
print(p, p + 4, "", "");
}
cout << "random_shuffling a word:"
<< endl;
string s("hello");
cout << s << endl;
for(int i = 0; i < 5; i++) {
random_shuffle(s.begin(), s.end());
cout << s << endl;
}
NString sa[] = { "a", "b",
"c", "d", "a", "b",
"c", "d", "a",
"b", "c", "d", "a", "b",
"c"};
const int SASZ = sizeof sa / sizeof *sa;
vector<NString> ns(sa, sa + SASZ);
print(ns.begin(), ns.end(),
"ns", " ");
vector<NString>::iterator it =
partition(ns.begin(), ns.end(),
bind2nd(greater<NString>(),
"b"));
cout << "Partition point: " <<
*it << endl;
print(ns.begin(), ns.end(), "", "
");
// Reload vector:
copy(sa, sa + SASZ, ns.begin());
it = stable_partition(ns.begin(), ns.end(),
bind2nd(greater<NString>(), "b"));
cout << "Stable partition" <<
endl;
cout << "Partition point: " <<
*it << endl;
print(ns.begin(), ns.end(), "", "
");
} ///:~The best way to see the results of this program is to run it. (You'll probably want to redirect the output to a file.)
The vector<int> v1 is initially loaded with a simple ascending sequence and printed. You'll see that the effect of copy_backward( ) (which copies into v2, which is the same size as v1) is the same as an ordinary copy. Again, copy_backward( ) does the same thing as copy( )—it just performs the operations in reverse order.
reverse_copy( ) actually does create a reversed copy, and reverse( ) performs the reversal in place. Next, swap_ranges( ) swaps the upper half of the reversed sequence with the lower half. The ranges could be smaller subsets of the entire vector, as long as they are of equivalent size.
After re-creating the ascending sequence, rotate( ) is demonstrated by rotating one third of v1 multiple times. A second rotate( ) example uses characters and just rotates two characters at a time. This also demonstrates the flexibility of both the STL algorithms and the print( ) template, since they can both be used with arrays of char as easily as with anything else.
To demonstrate next_permutation( ) and prev_permutation( ), a set of four characters “abcd” is permuted through all n! (n factorial) possible combinations. You'll see from the output that the permutations move through a strictly defined order (that is, permuting is a deterministic process).
A quick-and-dirty demonstration of random_shuffle( ) is to apply it to a string and see what words result. Because a string object has begin( ) and end( ) member functions that return the appropriate iterators, it too can be easily used with many of the STL algorithms. An array of char could also have been used.
Finally, the partition( ) and stable_partition( ) are demonstrated, using an array of NString. You'll note that the aggregate initialization expression uses char arrays, but NString has a char* constructor that is automatically used.
You'll see from the output that with the unstable partition, the objects are correctly above and below the partition point, but in no particular order; whereas with the stable partition, their original order is maintained.
2-4-3-5. Searching and replacing▲
All these algorithms are used for searching for one or more objects within a range defined by the first two iterator arguments.
InputIterator find(InputIterator
first, InputIterator last,
const EqualityComparable& value);
Searches for value within a range of elements. Returns an iterator in the range [first, last) that points to the first occurrence of value. If value isn't in the range, find( ) returns last. This is a linear search; that is, it starts at the beginning and looks at each sequential element without making any assumptions about the way the elements are ordered. In contrast, a binary_search( ) (defined later) works on a sorted sequence and can thus be much faster.
InputIterator find_if(InputIterator
first, InputIterator
last, Predicate pred);
Just like find( ), find_if( ) performs a linear search through the range. However, instead of searching for value, find_if( ) looks for an element such that the Predicate pred returns true when applied to that element. Returns last if no such element can be found.
ForwardIterator adjacent_find(ForwardIterator first,
ForwardIterator last);
ForwardIterator adjacent_find(ForwardIterator first,
ForwardIterator last, BinaryPredicate binary_pred);
Like find( ), performs a linear search through the range, but instead of looking for only one element, it searches for two adjacent elements that are equivalent. The first form of the function looks for two elements that are equivalent (via operator==). The second form looks for two adjacent elements that, when passed together to binary_pred, produce a true result. An iterator to the first of the two elements is returned if a pair is found; otherwise, last is returned.
ForwardIterator1 find_first_of(ForwardIterator1 first1,
ForwardIterator1 last1, ForwardIterator2 first2,
ForwardIterator2 last2);
ForwardIterator1 find_first_of(ForwardIterator1 first1,
ForwardIterator1 last1, ForwardIterator2 first2,
ForwardIterator2 last2, BinaryPredicate binary_pred);
Like find( ), performs a linear search through the range. Both forms search for an element in the second range that's equivalent to one in the first, the first form using operator==, and the second using the supplied predicate. In the second form, the current element from the first range becomes the first argument to binary_pred, and the element from the second range becomes the second argument.
ForwardIterator1 search(ForwardIterator1 first1,
ForwardIterator1 last1, ForwardIterator2 first2,
ForwardIterator2 last2);
ForwardIterator1 search(ForwardIterator1 first1,
ForwardIterator1 last1, ForwardIterator2 first2,
ForwardIterator2 last2 BinaryPredicate binary_pred);
Checks to see if the second range occurs (in the exact order of the second range) within the first range, and if so returns an iterator pointing to the place in the first range where the second range begins. Returns last1 if no subset can be found. The first form performs its test using operator==, and the second checks to see if each pair of objects being compared causes binary_pred to return true.
ForwardIterator1 find_end(ForwardIterator1 first1,
ForwardIterator1 last1, ForwardIterator2 first2,
ForwardIterator2 last2);
ForwardIterator1 find_end(ForwardIterator1 first1,
ForwardIterator1 last1, ForwardIterator2 first2,
ForwardIterator2 last2, BinaryPredicate binary_pred);
The forms and arguments are just like search( ) in that they look for the second range appearing as a subset of the first range, but while search( ) looks for the first occurrence of the subset, find_end( ) looks for the last occurrence and returns an iterator to its first element.
ForwardIterator search_n(ForwardIterator first,
ForwardIterator last, Size count, const T& value);
ForwardIterator search_n(ForwardIterator first,
ForwardIterator last, Size count, const T& value,
BinaryPredicate binary_pred);
Looks for a group of count consecutive values in [first, last) that are all equal to value (in the first form) or that all cause a return value of true when passed into binary_pred along with value (in the second form). Returns last if such a group cannot be found.
ForwardIterator min_element(ForwardIterator first,
ForwardIterator last);
ForwardIterator min_element(ForwardIterator first,
ForwardIterator last, BinaryPredicate binary_pred);
Returns an iterator pointing to the first occurrence of the “smallest” value in the range (as explained below—there may be multiple occurrences of this value.) Returns last if the range is empty. The first version performs comparisons with operator<, and the value r returned is such that *e < *r is false for every element e in the range [first, r). The second version compares using binary_pred, and the value r returned is such that binary_pred(*e, *r) is false for every element e in the range [first, r).
ForwardIterator max_element(ForwardIterator first,
ForwardIterator last);
ForwardIterator max_element(ForwardIterator first,
ForwardIterator last, BinaryPredicate binary_pred);
Returns an iterator pointing to the first occurrence of the largest value in the range. (There may be multiple occurrences of the largest value.) Returns last if the range is empty. The first version performs comparisons with operator<, and the value r returned is such that *r < *e is false for every element e in the range [first, r). The second version compares using binary_pred, and the value r returned is such that binary_pred(*r, *e) is false for every element e in the range [first, r).
void replace(ForwardIterator first, ForwardIterator last,
const T& old_value, const T& new_value);
void replace_if(ForwardIterator first, ForwardIterator
last, Predicate pred, const T& new_value);
OutputIterator replace_copy(InputIterator first,
InputIterator last, OutputIterator result, const T&
old_value, const T& new_value);
OutputIterator replace_copy_if(InputIterator first,
InputIterator last, OutputIterator result, Predicate
pred, const T& new_value);
Each of the “replace” forms moves through the range [first, last), finding values that match a criterion and replacing them with new_value. Both replace( ) and replace_copy( ) simply look for old_value to replace; replace_if( ) and replace_copy_if( ) look for values that satisfy the predicate pred. The “copy” versions of the functions do not modify the original range but instead make a copy with the replacements into result (incrementing result after each assignment).
Example
To provide easy viewing of the results, this example manipulates vectors of int. Again, not every possible version of each algorithm is shown. (Some that should be obvious have been omitted.)
//: C06:SearchReplace.cpp
// The STL search and replace algorithms.
#include <algorithm>
#include <functional>
#include <vector>
#include "PrintSequence.h"
using namespace std;
struct PlusOne {
bool operator()(int i, int j) { return j == i + 1; }
};
class MulMoreThan {
int value;
public:
MulMoreThan(int val) : value(val) {}
bool operator()(int v, int m) { return v * m >
value; }
};
int main() {
int a[] = { 1, 2, 3, 4, 5, 6, 6, 7, 7, 7,
8, 8, 8, 8, 11, 11, 11, 11, 11 };
const int ASZ = sizeof a / sizeof *a;
vector<int> v(a, a + ASZ);
print(v.begin(), v.end(), "v", "
");
vector<int>::iterator it = find(v.begin(),
v.end(), 4);
cout << "find: " << *it
<< endl;
it = find_if(v.begin(), v.end(),
bind2nd(greater<int>(), 8));
cout << "find_if: " << *it
<< endl;
it = adjacent_find(v.begin(), v.end());
while(it != v.end()) {
cout << "adjacent_find: " <<
*it
<< ", " << *(it + 1)
<< endl;
it = adjacent_find(it + 1, v.end());
}
it = adjacent_find(v.begin(), v.end(), PlusOne());
while(it != v.end()) {
cout << "adjacent_find PlusOne: "
<< *it
<< ", " << *(it + 1)
<< endl;
it = adjacent_find(it + 1, v.end(), PlusOne());
}
int b[] = { 8, 11 };
const int BSZ = sizeof b / sizeof *b;
print(b, b + BSZ, "b", " ");
it = find_first_of(v.begin(), v.end(), b, b + BSZ);
print(it, it + BSZ, "find_first_of", "
");
it = find_first_of(v.begin(), v.end(),
b, b + BSZ, PlusOne());
print(it,it + BSZ,"find_first_of
PlusOne"," ");
it = search(v.begin(), v.end(), b, b + BSZ);
print(it, it + BSZ, "search", "
");
int c[] = { 5, 6, 7 };
const int CSZ = sizeof c / sizeof *c;
print(c, c + CSZ, "c", " ");
it = search(v.begin(), v.end(), c, c + CSZ,
PlusOne());
print(it, it + CSZ,"search PlusOne", "
");
int d[] = { 11, 11, 11 };
const int DSZ = sizeof d / sizeof *d;
print(d, d + DSZ, "d", " ");
it = find_end(v.begin(), v.end(), d, d + DSZ);
print(it, v.end(),"find_end", "
");
int e[] = { 9, 9 };
print(e, e + 2, "e", "
");
it = find_end(v.begin(),
v.end(), e, e + 2, PlusOne());
print(it, v.end(),"find_end PlusOne","
");
it = search_n(v.begin(), v.end(), 3, 7);
print(it, it + 3, "search_n 3, 7", "
");
it = search_n(v.begin(), v.end(),
6, 15, MulMoreThan(100));
print(it, it + 6,
"search_n 6, 15, MulMoreThan(100)",
" ");
cout << "min_element: "
<< *min_element(v.begin(), v.end())
<< endl;
cout << "max_element: "
<< *max_element(v.begin(), v.end())
<< endl;
vector<int> v2;
replace_copy(v.begin(), v.end(),
back_inserter(v2), 8, 47);
print(v2.begin(), v2.end(), "replace_copy 8
-> 47", " ");
replace_if(v.begin(), v.end(),
bind2nd(greater_equal<int>(), 7), -1);
print(v.begin(), v.end(), "replace_if >= 7
-> -1", " ");
} ///:~The example begins with two predicates: PlusOne, which is a binary predicate that returns true if the second argument is equivalent to one plus the first argument; and MulMoreThan, which returns true if the first argument times the second argument is greater than a value stored in the object. These binary predicates are used as tests in the example.
In main( ), an array a is created and fed to the constructor for vector<int> v. This vector is the target for the search and replace activities, and you'll note that there are duplicate elements—these are discovered by some of the search/replace routines.
The first test demonstrates find( ), discovering the value 4 in v. The return value is the iterator pointing to the first instance of 4, or the end of the input range (v.end( )) if the search value is not found.
The find_if( ) algorithm uses a predicate to determine if it has discovered the correct element. In this example, this predicate is created on the fly using greater<int> (that is, “see if the first int argument is greater than the second”) and bind2nd( ) to fix the second argument to 8. Thus, it returns true if the value in v is greater than 8.
Since two identical objects appear next to each other in a number of cases in v, the test of adjacent_find( ) is designed to find them all. It starts looking from the beginning and then drops into a while loop, making sure that the iterator it has not reached the end of the input sequence (which would mean that no more matches can be found). For each match it finds, the loop prints the matches and then performs the next adjacent_find( ), this time using it + 1 as the first argument (this way, it will still find two pairs in a triple).
You might look at the while loop and think that you can do it a bit more cleverly, like this:
while(it != v.end()) {
cout << "adjacent_find: " <<
*it++
<< ", " << *it++
<< endl;
it = adjacent_find(it, v.end());
}This is exactly what we tried first. However, we did not get the output we expected, on any compiler. This is because there is no guarantee about when the increments occur in this expression.
The next test uses adjacent_find( ) with the PlusOne predicate, which discovers all the places where the next number in the sequence v changes from the previous by one. The same while approach finds all the cases.
The find_first_of( ) algorithm requires a second range of objects for which to hunt; this is provided in the array b. Because the first range and the second range in find_first_of( ) are controlled by separate template arguments, those ranges can refer to two different types of containers, as seen here. The second form of find_first_of( ) is also tested, using PlusOne.
The search( ) algorithm finds exactly the second range inside the first one, with the elements in the same order. The second form of search( ) uses a predicate, which is typically just something that defines equivalence, but it also presents some interesting possibilities—here, the PlusOne predicate causes the range { 4, 5, 6 } to be found.
The find_end( ) test discovers the last occurrence of the entire sequence { 11, 11, 11 }. To show that it has in fact found the last occurrence, the rest of v starting from it is printed.
The first search_n( ) test looks for 3 copies of the value 7, which it finds and prints. When using the second version of search_n( ), the predicate is ordinarily meant to be used to determine equivalence between two elements, but we've taken some liberties and used a function object that multiplies the value in the sequence by (in this case) 15 and checks to see if it's greater than 100. That is, the search_n( ) test says “find me 6 consecutive values that, when multiplied by 15, each produce a number greater than 100.” Not exactly what you normally expect to do, but it might give you some ideas the next time you have an odd searching problem.
The min_element( ) and max_element( ) algorithms are straightforward, but they look odd, as if the function is being dereferenced with a ‘*'. Actually, the returned iterator is being dereferenced to produce the value for printing.
To test replacements, replace_copy( ) is used first (so it doesn't modify the original vector) to replace all values of 8 with the value 47. Notice the use of back_inserter( ) with the empty vector v2. To demonstrate replace_if( ), a function object is created using the standard template greater_equal along with bind2nd to replace all the values that are greater than or equal to 7 with the value -1.
2-4-3-6. Comparing ranges▲
These algorithms provide ways to compare two ranges. At first glance, the operations they perform seem similar to the search( ) function. However, search( ) tells you where the second sequence appears within the first, and equal( ) and lexicographical_compare( ) simply tell you how two sequences compare. On the other hand, mismatch( ) does tell you where the two sequences go out of sync, but those sequences must be exactly the same length.
bool equal(InputIterator first1, InputIterator last1,
InputIterator first2);
bool equal(InputIterator first1, InputIterator last1,
InputIterator first2 BinaryPredicate binary_pred);
In both these functions, the first range is the typical one, [first1, last1). The second range starts at first2, but there is no “last2” because its length is determined by the length of the first range. The equal( ) function returns true if both ranges are exactly the same (the same elements in the same order). In the first case, the operator== performs the comparison, and in the second case binary_pred decides if two elements are the same.
bool lexicographical_compare(InputIterator1 first1,
InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2);
bool lexicographical_compare(InputIterator1 first1,
InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2, BinaryPredicate binary_pred);
These two functions determine if the first range is “lexicographically less” than the second. (They return true if range 1 is less than range 2, and false otherwise.) Lexicographical comparison, or “dictionary” comparison, means that the comparison is done in the same way that we establish the order of strings in a dictionary: one element at a time. The first elements determine the result if these elements are different, but if they're equal, the algorithm moves on to the next elements and looks at those, and so on until it finds a mismatch. At that point, it looks at the elements, and if the element from range 1 is less than the element from range two, lexicographical_compare( ) returns true; otherwise, it returns false. If it gets all the way through one range or the other (the ranges may be different lengths for this algorithm) without finding an inequality, range 1 is not less than range 2, so the function returns false.
If the two ranges are different lengths, a missing element in one range acts as one that “precedes” an element that exists in the other range, so “abc” precedes “abcd.” If the algorithm reaches the end of one of the ranges without a mismatch, then the shorter range comes first. In that case, if the shorter range is the first range, the result is true, otherwise it is false.
In the first version of the function, operator< performs the comparisons, and in the second version, binary_pred is used.
pair<InputIterator1,
InputIterator2>
mismatch(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2);
pair<InputIterator1, InputIterator2>
mismatch(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, BinaryPredicate binary_pred);
As in equal( ), the length of both ranges is exactly the same, so only the first iterator in the second range is necessary, and the length of the first range is used as the length of the second range. Whereas equal( ) just tells you whether the two ranges are the same, mismatch( ) tells you where they begin to differ. To accomplish this, you must be told (1) the element in the first range where the mismatch occurred and (2) the element in the second range where the mismatch occurred. These two iterators are packaged together into a pair object and returned. If no mismatch occurs, the return value is last1 combined with the past-the-end iterator of the second range. The pair template class is a struct with two elements denoted by the member names first and second and is defined in the <utility> header.
As in equal( ), the first function tests for equality using operator== while the second one uses binary_pred.
Example
Because the Standard C++ string class is built like a container (it has begin( ) and end( ) member functions that produce objects of type string::iterator), it can be used to conveniently create ranges of characters to test with the STL comparison algorithms. However, note that string has a fairly complete set of native operations, so look at the string class before using the STL algorithms to perform operations.
//: C06:Comparison.cpp
// The STL range comparison algorithms.
#include <algorithm>
#include <functional>
#include <string>
#include <vector>
#include "PrintSequence.h"
using namespace std;
int main() {
// Strings provide a convenient way to create
// ranges of characters, but you should
// normally look for native string operations:
string s1("This is a test");
string s2("This is a Test");
cout << "s1: " << s1 <<
endl << "s2: " << s2 << endl;
cout << "compare s1 & s1: "
<< equal(s1.begin(), s1.end(), s1.begin())
<< endl;
cout << "compare s1 & s2: "
<< equal(s1.begin(), s1.end(), s2.begin())
<< endl;
cout << "lexicographical_compare s1 &
s1: "
<< lexicographical_compare(s1.begin(),
s1.end(),
s1.begin(), s1.end()) << endl;
cout << "lexicographical_compare s1 &
s2: "
<< lexicographical_compare(s1.begin(),
s1.end(),
s2.begin(), s2.end()) << endl;
cout << "lexicographical_compare s2 &
s1: "
<< lexicographical_compare(s2.begin(),
s2.end(),
s1.begin(), s1.end()) << endl;
cout << "lexicographical_compare shortened
"
"s1 & full-length s2: "
<< endl;
string s3(s1);
while(s3.length() != 0) {
bool result = lexicographical_compare(
s3.begin(), s3.end(), s2.begin(),s2.end());
cout << s3 << endl << s2 <<
", result = "
<< result << endl;
if(result == true) break;
s3 = s3.substr(0, s3.length() - 1);
}
pair<string::iterator, string::iterator> p =
mismatch(s1.begin(), s1.end(), s2.begin());
print(p.first, s1.end(), "p.first",
"");
print(p.second, s2.end(),
"p.second","");
} ///:~Note that the only difference between s1 and s2 is the capital ‘T' in s2's “Test.” Comparing s1 and s1 for equality yields true, as expected, while s1 and s2 are not equal because of the capital ‘T'.
To understand the output of the lexicographical_compare( ) tests, remember two things: first, the comparison is performed character-by-character, and second, on our platform capital letters “precede” lowercase letters. In the first test, s1 is compared to s1. These are exactly equivalent. One is not lexicographically less than the other (which is what the comparison is looking for), and thus the result is false. The second test is asking “does s1 precede s2?” When the comparison gets to the ‘t' in “test”, it discovers that the lowercase ‘t' in s1 is “greater” than the uppercase ‘T' in s2, so the answer is again false. However, if we test to see whether s2 precedes s1, the answer is true.
To further examine lexicographical comparison, the next test in this example compares s1 with s2 again (which returned false before). But this time it repeats the comparison, trimming one character off the end of s1 (which is first copied into s3) each time through the loop until the test evaluates to true. What you'll see is that, as soon as the uppercase ‘T' is trimmed off s3 (the copy of s1), the characters, which are exactly equal up to that point, no longer count. Because s3 is shorter than s2, it lexicographically precedes s2.
The final test uses mismatch( ). To capture the return value, create the appropriate pair p, constructing the template using the iterator type from the first range and the iterator type from the second range (in this case, both string::iterators). To print the results, the iterator for the mismatch in the first range is p.first, and for the second range is p.second. In both cases, the range is printed from the mismatch iterator to the end of the range so you can see exactly where the iterator points.
2-4-3-7. Removing elements▲
Because of the genericity of the STL, the concept of removal is a bit constrained. Since elements can only be “removed” via iterators, and iterators can point to arrays, vectors, lists, and so on, it is not safe or reasonable to try to destroy the elements that are being removed and to change the size of the input range [first, last). (An array, for example, cannot have its size changed.) So instead, what the STL “remove” functions do is rearrange the sequence so that the “removed” elements are at the end of the sequence, and the “un-removed” elements are at the beginning of the sequence (in the same order that they were before, minus the removed elements—that is, this is a stable operation). Then the function will return an iterator to the “new last” element of the sequence, which is the end of the sequence without the removed elements and the beginning of the sequence of the removed elements. In other words, if new_last is the iterator that is returned from the “remove” function, [first, new_last) is the sequence without any of the removed elements, and [new_last, last) is the sequence of removed elements.
If you are simply using your sequence, including the removed elements, with more STL algorithms, you can just use new_last as the new past-the-end iterator. However, if you're using a resizable container c (not an array) and you want to eliminate the removed elements from the container, you can use erase( ) to do so, for example:
c.erase(remove(c.begin(), c.end(), value), c.end());You can also use the resize( ) member function that belongs to all standard sequences (more on this in the next chapter).
The return value of remove( ) is the new_last iterator, so erase( ) deletes all the removed elements from c.
The iterators in [new_last, last) are dereferenceable, but the element values are unspecified and should not be used.
ForwardIterator remove(ForwardIterator first,
ForwardIterator last, const T& value);
ForwardIterator remove_if(ForwardIterator first,
ForwardIterator last, Predicate pred);
OutputIterator remove_copy(InputIterator first,
InputIterator last, OutputIterator result, const T&
value);
OutputIterator remove_copy_if(InputIterator first,
InputIterator last, OutputIterator result, Predicate
pred);
Each of the “remove” forms moves through the range [first, last), finding values that match a removal criterion and copying the unremoved elements over the removed elements (thus effectively removing them). The original order of the unremoved elements is maintained. The return value is an iterator pointing past the end of the range that contains none of the removed elements. The values that this iterator points to are unspecified.
The “if” versions pass each element to pred( ) to determine whether it should be removed. (If pred( ) returns true, the element is removed.) The “copy” versions do not modify the original sequence, but instead copy the unremoved values into a range beginning at result and return an iterator indicating the past-the-end value of this new range.
ForwardIterator unique(ForwardIterator first,
ForwardIterator last);
ForwardIterator unique(ForwardIterator first,
ForwardIterator last, BinaryPredicate binary_pred);
OutputIterator unique_copy(InputIterator first,
InputIterator last, OutputIterator result);
OutputIterator unique_copy(InputIterator first,
InputIterator last, OutputIterator result,
BinaryPredicate binary_pred);
Each of the “unique” functions moves through the range [first, last), finding adjacent values that are equivalent (that is, duplicates) and “removing” the duplicate elements by copying over them. The original order of the unremoved elements is maintained. The return value is an iterator pointing past the end of the range that has the adjacent duplicates removed.
Because only duplicates that are adjacent are removed, it's likely that you'll want to call sort( ) before calling a “unique” algorithm, since that will guarantee that all the duplicates are removed.
For each iterator value i in the input range, the versions containing binary_pred call:
binary_pred(*i, *(i-1));and if the result is true, *i is considered a duplicate.
The “copy” versions do not modify the original sequence, but instead copy the unremoved values into a range beginning at result and return an iterator indicating the past-the-end value of this new range.
Example
This example gives a visual demonstration of the way the “remove” and “unique” functions work.
//: C06:Removing.cpp
// The removing algorithms.
//{L} Generators
#include <algorithm>
#include <cctype>
#include <string>
#include "Generators.h"
#include "PrintSequence.h"
using namespace std;
struct IsUpper {
bool operator()(char c) { return isupper(c); }
};
int main() {
string v;
v.resize(25);
generate(v.begin(), v.end(), CharGen());
print(v.begin(), v.end(), "v original",
"");
// Create a set of the characters in v:
string us(v.begin(), v.end());
sort(us.begin(), us.end());
string::iterator it = us.begin(), cit = v.end(),
uend = unique(us.begin(), us.end());
// Step through and remove everything:
while(it != uend) {
cit = remove(v.begin(), cit, *it);
print(v.begin(), v.end(), "Complete v",
"");
print(v.begin(), cit, "Pseudo v ", "
");
cout << "Removed element:\t"
<< *it
<< "\nPsuedo Last Element:\t"
<< *cit << endl << endl;
++it;
}
generate(v.begin(), v.end(), CharGen());
print(v.begin(), v.end(), "v",
"");
cit = remove_if(v.begin(), v.end(), IsUpper());
print(v.begin(), cit, "v after remove_if
IsUpper", " ");
// Copying versions are not shown for remove()
// and remove_if().
sort(v.begin(), cit);
print(v.begin(), cit, "sorted", "
");
string v2;
v2.resize(cit - v.begin());
unique_copy(v.begin(), cit, v2.begin());
print(v2.begin(), v2.end(), "unique_copy",
" ");
// Same behavior:
cit = unique(v.begin(), cit, equal_to<char>());
print(v.begin(), cit, "unique
equal_to<char>", " ");
} ///:~Thestring v is a container of characters filled with randomly generated characters. Each character is used in a remove statement, but the entire string v is displayed each time so you can see what happens to the rest of the range, after the resulting endpoint (which is stored in cit).
To demonstrate remove_if( ), the standard C library function isupper( ) (in <cctype>)is called inside the function object class IsUpper, an object of which ispassed as the predicate for remove_if( ).This returns true only if a character is uppercase, so only lowercase characters will remain. Here, the end of the range is used in the call to print( ) so only the remaining elements will appear. The copying versions of remove( ) and remove_if( ) are not shown because they are a simple variation on the noncopying versions, which you should be able to use without an example.
The range of lowercase letters is sorted in preparation for testing the “unique” functions. (The “unique” functions are not undefined if the range isn't sorted, but it's probably not what you want.) First, unique_copy( ) puts the unique elements into a new vector using the default element comparison, and then uses the form of unique( ) that takes a predicate. The predicate is the built-in function object equal_to( ), which produces the same results as the default element comparison.
2-4-3-8. Sorting and operations on sorted ranges▲
A significant category of STL algorithms must operate on a sorted range. STL provides a number of separate sorting algorithms, depending on whether the sort should be stable, partial, or just regular (non-stable). Oddly enough, only the partial sort has a copying version. If you're using another sort and you need to work on a copy, you'll have to make your own copy before sorting.
Once your sequence is sorted, you can perform many operations on that sequence, from simply locating an element or group of elements to merging with another sorted sequence or manipulating sequences as mathematical sets.
Each algorithm involved with sorting or operations on sorted sequences has two versions. The first uses the object's own operator< to perform the comparison, and the second uses operator( )(a, b) to determine the relative order of a and b. Other than this, there are no differences, so this distinction will not be pointed out in the description of each algorithm.
Sorting
The sort algorithms require ranges delimited by random-access iterators, such as a vector or deque. The list container has its own built-in sort( ) function, since it only supports bi-directional iteration.
void sort(RandomAccessIterator first, RandomAccessIterator
last);
void sort(RandomAccessIterator first, RandomAccessIterator
last, StrictWeakOrdering binary_pred);
Sorts [first, last) into ascending order. The first form uses operator< and the second form uses the supplied comparator object to determine the order.
void stable_sort(RandomAccessIterator first,
RandomAccessIterator last);
void stable_sort(RandomAccessIterator first,
RandomAccessIterator last, StrictWeakOrdering
binary_pred);
Sorts [first, last) into ascending order, preserving the original ordering of equivalent elements. (This is important if elements can be equivalent but not identical.)
void partial_sort(RandomAccessIterator first,
RandomAccessIterator middle, RandomAccessIterator last);
void partial_sort(RandomAccessIterator first,
RandomAccessIterator middle, RandomAccessIterator last,
StrictWeakOrdering binary_pred);
Sorts the number of elements from [first, last) that can be placed in the range [first, middle). The rest of the elements end up in [middle, last) and have no guaranteed order.
RandomAccessIterator partial_sort_copy(InputIterator first,
InputIterator last, RandomAccessIterator result_first,
RandomAccessIterator result_last);
RandomAccessIterator partial_sort_copy(InputIterator first,
InputIterator last, RandomAccessIterator result_first,
RandomAccessIterator result_last, StrictWeakOrdering
binary_pred);
Sorts the number of elements from [first, last) that can be placed in the range [result_first, result_last) and copies those elements into [result_first, result_last). If the range [first, last) is smaller than [result_first, result_last), the smaller number of elements is used.
void nth_element(RandomAccessIterator first,
RandomAccessIterator nth, RandomAccessIterator last);
void nth_element(RandomAccessIterator first,
RandomAccessIterator nth, RandomAccessIterator last,
StrictWeakOrdering binary_pred);
Just like partial_sort( ), nth_element( ) partially orders a range of elements. However, it's much “less ordered” than partial_sort( ). The only guarantee from nth_element( ) is that whatever location you choose will become a dividing point. All the elements in the range [first, nth) will pair-wise satisfy the binary predicate (operator< by default, as usual),and all the elements in the range (nth, last] will not. However, neither subrange is in any particular order, unlike partial_sort( ) which has the first range in sorted order.
If all you need is this very weak ordering (if, for example, you're determining medians, percentiles, and so on), this algorithm is faster than partial_sort( ).
Locating elements in sorted ranges
Once a range is sorted, you can use a group of operations to find elements within those ranges. In the following functions, there are always two forms. One assumes that the intrinsic operator< performs the sort, and the second operator must be used if some other comparison function object performs the sort. You must use the same comparison for locating elements as you do to perform the sort; otherwise, the results are undefined. In addition, if you try to use these functions on unsorted ranges, the results will be undefined.
bool binary_search(ForwardIterator first, ForwardIterator
last, const T& value);
bool binary_search(ForwardIterator first, ForwardIterator
last, const T& value, StrictWeakOrdering binary_pred);
Tells you whether value appears in the sorted range [first, last).
ForwardIterator lower_bound(ForwardIterator first,
ForwardIterator last, const T& value);
ForwardIterator lower_bound(ForwardIterator first,
ForwardIterator last, const T& value, StrictWeakOrdering
binary_pred);
Returns an iterator indicating the first occurrence of value in the sorted range [first, last). If value is not present, an iterator to where it would fit in the sequence is returned.
ForwardIterator upper_bound(ForwardIterator first,
ForwardIterator last, const T& value);
ForwardIterator upper_bound(ForwardIterator first,
ForwardIterator last, const T& value, StrictWeakOrdering
binary_pred);
Returns an iterator indicating one past the last occurrence of value in the sorted range [first, last). If value is not present, an iterator to where it would fit in the sequence is returned.
pair<ForwardIterator,
ForwardIterator> equal_range(ForwardIterator first, ForwardIterator last,
const T& value);
pair<ForwardIterator, ForwardIterator> equal_range(ForwardIterator
first, ForwardIterator last,
const T& value, StrictWeakOrdering binary_pred);
Essentially combines lower_bound( ) and upper_bound( ) to return a pair indicating the first and one-past-the-last occurrences of value in the sorted range [first, last). Both iterators indicate the location where value would fit if it is not found.
You may find it surprising that the binary search algorithms take a forward iterator instead of a random access iterator. (Most explanations of binary search use indexing.) Remember that a random access iterator “is-a” forward iterator, and can be used wherever the latter is specified. If the iterator passed to one of these algorithms in fact supports random access, then the efficient logarithmic-time procedure is used, otherwise a linear search is performed.(96)
Example
Thefollowing example turns each input word into an NString and adds it to a vector<NString>. The vector is then used to demonstrate the various sorting and searching algorithms.
//: C06:SortedSearchTest.cpp
// Test searching in sorted ranges.
// NString
#include <algorithm>
#include <cassert>
#include <ctime>
#include <cstdlib>
#include <cstddef>
#include <fstream>
#include <iostream>
#include <iterator>
#include <vector>
#include "NString.h"
#include "PrintSequence.h"
#include "../require.h"
using namespace std;
int main(int argc, char* argv[]) {
typedef vector<NString>::iterator sit;
char* fname = "Test.txt";
if(argc > 1) fname = argv[1];
ifstream in(fname);
assure(in, fname);
srand(time(0));
cout.setf(ios::boolalpha);
vector<NString> original;
copy(istream_iterator<string>(in),
istream_iterator<string>(),
back_inserter(original));
require(original.size() >= 4, "Must have four
elements");
vector<NString> v(original.begin(),
original.end()),
w(original.size() / 2);
sort(v.begin(), v.end());
print(v.begin(), v.end(), "sort");
v = original;
stable_sort(v.begin(), v.end());
print(v.begin(), v.end(), "stable_sort");
v = original;
sit it = v.begin(), it2;
// Move iterator to middle
for(size_t i = 0; i < v.size() / 2; i++)
++it;
partial_sort(v.begin(), it, v.end());
cout << "middle = " << *it
<< endl;
print(v.begin(), v.end(), "partial_sort");
v = original;
// Move iterator to a quarter position
it = v.begin();
for(size_t i = 0; i < v.size() / 4; i++)
++it;
// Less elements to copy from than to the destination
partial_sort_copy(v.begin(), it, w.begin(), w.end());
print(w.begin(), w.end(),
"partial_sort_copy");
// Not enough room in destination
partial_sort_copy(v.begin(), v.end(),
w.begin(),w.end());
print(w.begin(), w.end(), "w
partial_sort_copy");
// v remains the same through all this process
assert(v == original);
nth_element(v.begin(), it, v.end());
cout << "The nth_element = " <<
*it << endl;
print(v.begin(), v.end(), "nth_element");
string f = original[rand() % original.size()];
cout << "binary search: "
<< binary_search(v.begin(), v.end(), f)
<< endl;
sort(v.begin(), v.end());
it = lower_bound(v.begin(), v.end(), f);
it2 = upper_bound(v.begin(), v.end(), f);
print(it, it2, "found range");
pair<sit, sit> ip = equal_range(v.begin(),
v.end(), f);
print(ip.first, ip.second, "equal_range");
} ///:~This example uses the NString class seen earlier, which stores an occurrence number with copies of a string. The call to stable_sort( ) shows how the original order for objects with equal strings is preserved. You can also see what happens during a partial sort (the remaining unsorted elements are in no particular order). There is no “partial stable sort.”
Notice in the call to nth_element( ) that, whatever the nth element turns out to be (which will vary from one run to another because of URandGen), the elements before that are less, and after that are greater, but the elements have no particular order other than that. Because of URandGen, there are no duplicates, but if you use a generator that allows duplicates, you'll see that the elements before the nth element will be less than or equal to the nth element.
This example also illustrates all three binary search algorithms. As advertised, lower_bound( ) refers to the first element in the sequence equal to a given key, upper_bound( ) points one past the last, and equal_range( ) returns both results as a pair.
Merging sorted ranges
As before, the first form of each function assumes that the intrinsic operator< performs the sort. The second form must be used if some other comparison function object performs the sort. You must use the same comparison for locating elements as you do to perform the sort; otherwise, the results are undefined. In addition, if you try to use these functions on unsorted ranges, the results will be undefined.
OutputIterator merge(InputIterator1 first1, InputIterator1
last1, InputIterator2 first2, InputIterator2 last2,
OutputIterator result);
OutputIterator merge(InputIterator1 first1, InputIterator1
last1, InputIterator2 first2, InputIterator2 last2,
OutputIterator result, StrictWeakOrdering binary_pred);
Copies elements from [first1, last1) and [first2, last2) into result, such that the resulting range is sorted in ascending order. This is a stable operation.
void inplace_merge(BidirectionalIterator first,
BidirectionalIterator middle, BidirectionalIterator
last);
void inplace_merge(BidirectionalIterator first,
BidirectionalIterator middle, BidirectionalIterator last,
StrictWeakOrdering binary_pred);
This assumes that [first, middle) and [middle, last) are each sorted ranges in the same sequence. The two ranges are merged so that the resulting range [first, last) contains the combined ranges in sorted order.
Example
It's easier to see what goes on with merging if ints are used. The following example also emphasizes how the algorithms (and our own print template) work with arrays as well as containers:
//: C06:MergeTest.cpp
// Test merging in sorted ranges.
//{L} Generators
#include <algorithm>
#include "PrintSequence.h"
#include "Generators.h"
using namespace std;
int main() {
const int SZ = 15;
int a[SZ*2] = {0};
// Both ranges go in the same array:
generate(a, a + SZ, SkipGen(0, 2));
a[3] = 4;
a[4] = 4;
generate(a + SZ, a + SZ*2, SkipGen(1, 3));
print(a, a + SZ, "range1", " ");
print(a + SZ, a + SZ*2, "range2", "
");
int b[SZ*2] = {0}; // Initialize all to zero
merge(a, a + SZ, a + SZ, a + SZ*2, b);
print(b, b + SZ*2, "merge", " ");
// Reset b
for(int i = 0; i < SZ*2; i++)
b[i] = 0;
inplace_merge(a, a + SZ, a + SZ*2);
print(a, a + SZ*2, "inplace_merge", "
");
int* end = set_union(a, a + SZ, a + SZ, a + SZ*2, b);
print(b, end, "set_union", " ");
} ///:~In main( ), instead of creating two separate arrays, both ranges are created end to end in the array a. (This will come in handy for the inplace_merge.) The first call to merge( ) places the result in a different array, b. For comparison, set_union( ) is also called, which has the same signature and similar behavior, except that it removes duplicates from the second set. Finally, inplace_merge( ) combines both parts of a.
Set operations on sorted ranges
Once ranges have been sorted, you can perform mathematical set operations on them.
bool includes(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2);
bool includes(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2,
StrictWeakOrdering binary_pred);
Returns true if [first2, last2) is a subset of [first1, last1). Neither range is required to hold only unique elements, but if [first2, last2) holds n elements of a particular value, [first1, last1) must also hold at least n elements if the result is to be true.
OutputIterator set_union(InputIterator1 first1,
InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2, OutputIterator result);
OutputIterator set_union(InputIterator1 first1,
InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2, OutputIterator result,
StrictWeakOrdering binary_pred);
Creates the mathematical union of two sorted ranges in the result range, returning the end of the output range. Neither input range is required to hold only unique elements, but if a particular value appears multiple times in both input sets, the resulting set will contain the larger number of identical values.
OutputIterator set_intersection(InputIterator1 first1,
InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2, OutputIterator result);
OutputIterator set_intersection(InputIterator1 first1,
InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2, OutputIterator result,
StrictWeakOrdering binary_pred);
Produces, in result, the intersection of the two input sets, returning the end of the output range—that is, the set of values that appear in both input sets. Neither input range is required to hold only unique elements, but if a particular value appears multiple times in both input sets, the resulting set will contain the smaller number of identical values.
OutputIterator set_difference(InputIterator1 first1,
InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2, OutputIterator result);
OutputIterator set_difference(InputIterator1 first1,
InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2, OutputIterator result,
StrictWeakOrdering binary_pred);
Produces, in result, the mathematical set difference, returning the end of the output range. All the elements that are in [first1, last1) but not in [first2, last2) are placed in the result set. Neither input range is required to hold only unique elements, but if a particular value appears multiple times in both input sets (n times in set 1 and m times in set 2), the resulting set will contain max(n-m, 0) copies of that value.
OutputIterator set_symmetric_difference(InputIterator1
first1, InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2, OutputIterator result);
OutputIterator set_symmetric_difference(InputIterator1
first1, InputIterator1 last1, InputIterator2 first2,
InputIterator2 last2, OutputIterator result,
StrictWeakOrdering binary_pred);
Constructs, in result, the set containing:
- All the elements in set 1 that are not in set 2.
- All the elements in set 2 that are not in set 1.
Neither input range is required to hold only unique elements, but if a particular value appears multiple times in both input sets (n times in set 1 and m times in set 2), the resulting set will contain abs(n-m) copies of that value, where abs( ) is the absolute value. The return value is the end of the output range.
Example
It's easiest to see the set operations demonstrated using simple vectors of characters. These characters are randomly generated and then sorted, but the duplicates are retained so that you can see what the set operations do when there are duplicates.
//: C06:SetOperations.cpp
// Set operations on sorted ranges.
//{L} Generators
#include <algorithm>
#include <vector>
#include "Generators.h"
#include "PrintSequence.h"
using namespace std;
int main() {
const int SZ = 30;
char v[SZ + 1], v2[SZ + 1];
CharGen g;
generate(v, v + SZ, g);
generate(v2, v2 + SZ, g);
sort(v, v + SZ);
sort(v2, v2 + SZ);
print(v, v + SZ, "v",
"");
print(v2, v2 + SZ, "v2", "");
bool b = includes(v, v + SZ, v + SZ/2, v + SZ);
cout.setf(ios::boolalpha);
cout << "includes: " << b
<< endl;
char v3[SZ*2 + 1], *end;
end = set_union(v, v + SZ, v2, v2 + SZ, v3);
print(v3, end, "set_union", "");
end = set_intersection(v, v + SZ, v2, v2 + SZ, v3);
print(v3, end, "set_intersection",
"");
end = set_difference(v, v + SZ, v2, v2 + SZ, v3);
print(v3, end, "set_difference",
"");
end = set_symmetric_difference(v, v + SZ,
v2, v2 + SZ, v3);
print(v3, end,
"set_symmetric_difference","");
} ///:~After v and v2 are generated, sorted, and printed, the includes( ) algorithm is tested by seeing if the entire range of v contains the last half of v. It does, so the result should always be true. The array v3 holds the output of set_union( ), set_intersection( ), set_difference( ), and set_symmetric_difference( ), and the results of each are displayed so you can ponder them and convince yourself that the algorithms work as promised.
2-4-3-9. Heap operations▲
A heap is an array-like data structure used to implement a “priority queue,” which is just a range that is organized in a way that accommodates retrieving elements by priority according to some comparison function. The heap operations in the standard library allow a sequence to be treated as a “heap” data structure, which always efficiently returns the element of highest priority, without fully ordering the entire sequence.
As with the “sort” operations, there are two versions of each function. The first uses the object's own operator< to perform the comparison; the second uses an additional StrictWeakOrdering object's operator( )(a, b) to compare two objects for a <b.
void make_heap(RandomAccessIterator first,
RandomAccessIterator last);
void make_heap(RandomAccessIterator first,
RandomAccessIterator last,
StrictWeakOrdering binary_pred);
Turns an arbitrary range into a heap.
void push_heap(RandomAccessIterator first,
RandomAccessIterator last);
void push_heap(RandomAccessIterator first,
RandomAccessIterator last,
StrictWeakOrdering binary_pred);
Adds the element *(last-1) to the heap determined by the range [first, last-1). In other words, it places the last element in its proper location in the heap.
void pop_heap(RandomAccessIterator first,
RandomAccessIterator last);
void pop_heap(RandomAccessIterator first,
RandomAccessIterator last,
StrictWeakOrdering binary_pred);
Places the largest element (which is actually in *first, before the operation, because of the way heaps are defined) into the position *(last-1)and reorganizes the remaining range so that it's still in heap order. If you simply grabbed *first, the next element would not be the next-largest element; so you must use pop_heap( ) if you want to maintain the heap in its proper priority-queue order.
void sort_heap(RandomAccessIterator first,
RandomAccessIterator last);
void sort_heap(RandomAccessIterator first,
RandomAccessIterator last,
StrictWeakOrdering binary_pred);
This could be thought of as the complement to make_heap( ). It takes a range that is in heap order and turns it into ordinary sorted order, so it is no longer a heap. That means that if you call sort_heap( ), you can no longer use push_heap( ) or pop_heap( ) on that range. (Rather, you can use those functions, but they won't do anything sensible.) This is not a stable sort.
2-4-3-10. Applying an operation to each element in a range▲
These algorithms move through the entire range and perform an operation on each element. They differ in what they do with the results of that operation: for_each( ) discards the return value of the operation, and transform( ) places the results of each operation into a destination sequence (which can be the original sequence).
UnaryFunction for_each(InputIterator first, InputIterator last, UnaryFunction f);
Applies the function object f to each element in [first, last), discarding the return value from each individual application of f. If f is just a function pointer, you are typically not interested in the return value; but if f is an object that maintains some internal state, it can capture the combined return value of being applied to the range. The final return value of for_each( ) is f.
OutputIterator transform(InputIterator first, InputIterator
last, OutputIterator result, UnaryFunction f);
OutputIterator transform(InputIterator1 first,
InputIterator1 last, InputIterator2 first2,
OutputIterator result, BinaryFunction f);
Like for_each( ), transform( ) applies a function object f to each element in the range [first, last). However, instead of discarding the result of each function call, transform( ) copies the result (using operator=) into *result, incrementing result after each copy. (The sequence pointed to by result must have enough storage; otherwise, use an inserter to force insertions instead of assignments.)
The first form of transform( ) simply calls f(*first), where first ranges through the input sequence. Similarly, the second form calls f(*first1, *first2).(Note that the length of the second input range is determined by the length of the first.) The return value in both cases is the past-the-end iterator for the resulting output range.
Examples
Since much of what you do with objects in a container is to apply an operation to all those objects, these are fairly important algorithms and merit several illustrations.
First, consider for_each( ). This sweeps through the range, pulling out each element and passing it as an argument as it calls whatever function object it's been given. Thus, for_each( ) performs operations that you might normally write out by hand. If you look in your compiler's header file at the template defining for_each( ), you'll see something like this:
template<class InputIterator, class Function>
Function for_each(InputIterator first, InputIterator
last,
Function f) {
while(first != last)
f(*first++);
return f;
}The following example shows several ways this template can be expanded. First, we need a class that keeps track of its objects so we can know that it's being properly destroyed:
//: C06:Counted.h
// An object that keeps track of itself.
#ifndef COUNTED_H
#define COUNTED_H
#include <vector>
#include <iostream>
class Counted {
static int count;
char* ident;
public:
Counted(char* id) : ident(id) { ++count; }
~Counted() {
std::cout << ident << " count =
"
<< --count << std::endl;
}
};
class CountedVector : public
std::vector<Counted*> {
public:
CountedVector(char* id) {
for(int i = 0; i < 5; i++)
push_back(new Counted(id));
}
};
#endif // COUNTED_H ///:~//: C06:Counted.cpp {O}
#include "Counted.h"
int Counted::count = 0;
///:~The class Counted keeps a static count of the number of Counted objects that have been created, and notifies you as they are destroyed.(97) In addition, each Counted keeps a char* identifier to make tracking the output easier.
The CountedVector is derived from vector<Counted*>, and in the constructor it creates some Counted objects, handing each one your desired char*. The CountedVector makes testing quite simple, as you can see here:
//: C06:ForEach.cpp {-mwcc}
// Use of STL for_each() algorithm.
//{L} Counted
#include <algorithm>
#include <iostream>
#include "Counted.h"
using namespace std;
// Function object:
template<class T> class DeleteT {
public:
void operator()(T* x) { delete x; }
};
// Template function:
template<class T> void wipe(T* x) { delete x; }
int main() {
CountedVector B("two");
for_each(B.begin(), B.end(), DeleteT<Counted>());
CountedVector C("three");
for_each(C.begin(), C.end(), wipe<Counted>);
} ///:~Since this is obviously something you might want to do a lot, why not create an algorithm to delete all the pointers in a container? You could use transform( ). The value of transform( ) over for_each( ) is that transform( ) assigns the result of calling the function object into a resulting range, which can actually be the input range. That case means a literal transformation for the input range, since each element would be a modification of its previous value. In this example, this approach would be especially useful since it's more appropriate to assign to each pointer the safe value of zero after calling delete for that pointer. Transform( ) can easily do this:
//: C06:Transform.cpp {-mwcc}
// Use of STL transform() algorithm.
//{L} Counted
#include <iostream>
#include <vector>
#include <algorithm>
#include "Counted.h"
using namespace std;
template<class T> T* deleteP(T* x) { delete x;
return 0; }
template<class T> struct Deleter {
T* operator()(T* x) { delete x; return 0; }
};
int main() {
CountedVector cv("one");
transform(cv.begin(), cv.end(), cv.begin(),
deleteP<Counted>);
CountedVector cv2("two");
transform(cv2.begin(), cv2.end(), cv2.begin(),
Deleter<Counted>());
} ///:~This shows both approaches: using a template function or a templatized function object. After the call to transform( ), the vector contains five null pointers, which is safer since any duplicate deletes will have no effect.
One thing you cannot do is delete every pointer in a collection without wrapping the call to delete inside a function or an object. That is, you do the following:
for_each(a.begin(), a.end(), ptr_fun(operator delete));This has the same problem as the call to destroy( ) did earlier: operator delete( ) takes a void*, but iterators aren't pointers. Even if you could make it compile, what you'd get is a sequence of calls to the function that releases the storage. You will not get the effect of calling delete for each pointer in a, however—the destructor will not be called. This is typically not what you want, so you will need to wrap your calls to delete.
In the previous example of for_each( ), the return value of the algorithm was ignored. This return value is the function that is passed into for_each( ). If the function is just a pointer to a function, the return value is not very useful, but if it is a function object, that function object may have internal member data that it uses to accumulate information about all the objects that it sees during for_each( ).
For example, consider a simple model of inventory. Each Inventory object has the type of product it represents (here, single characters will be used for product names), the quantity of that product, and the price of each item:
//: C06:Inventory.h
#ifndef INVENTORY_H
#define INVENTORY_H
#include <iostream>
#include <cstdlib>
using std::rand;
class Inventory {
char item;
int quantity;
int value;
public:
Inventory(char it, int quant, int val)
: item(it), quantity(quant), value(val) {}
// Synthesized operator= & copy-constructor OK
char getItem() const { return item; }
int getQuantity() const { return quantity; }
void setQuantity(int q) { quantity = q; }
int getValue() const { return value; }
void setValue(int val) { value = val; }
friend std::ostream& operator<<(
std::ostream& os, const Inventory& inv) {
return os << inv.item << ": "
<< "quantity " <<
inv.quantity
<< ", value " << inv.value;
}
};
// A generator:
struct InvenGen {
Inventory operator()() {
static char c = 'a';
int q = rand() % 100;
int v = rand() % 500;
return Inventory(c++, q, v);
}
};
#endif // INVENTORY_H ///:~Member functions get the item name and get and set quantity and value. An operator<< prints the Inventory object to an ostream. A generator creates objects that have sequentially labeled items and random quantities and values.
To find out the total number of items and total value, you can create a function object to use with for_each( ) that has data members to hold the totals:
//: C06:CalcInventory.cpp
// More use of for_each().
#include <algorithm>
#include <ctime>
#include <vector>
#include "Inventory.h"
#include "PrintSequence.h"
using namespace std;
// To calculate inventory totals:
class InvAccum {
int quantity;
int value;
public:
InvAccum() : quantity(0), value(0) {}
void operator()(const Inventory& inv) {
quantity += inv.getQuantity();
value += inv.getQuantity() * inv.getValue();
}
friend ostream&
operator<<(ostream& os, const InvAccum&
ia) {
return os << "total quantity: "
<< ia.quantity
<< ", total value: " <<
ia.value;
}
};
int main() {
vector<Inventory> vi;
srand(time(0)); // Randomize
generate_n(back_inserter(vi), 15, InvenGen());
print(vi.begin(), vi.end(), "vi");
InvAccum ia = for_each(vi.begin(),vi.end(),
InvAccum());
cout << ia << endl;
} ///:~InvAccum's operator( ) takes a single argument, as required by for_each( ). As for_each( ) moves through its range, it takes each object in that range and passes it to InvAccum::operator( ), which performs calculations and saves the result. At the end of this process, for_each( ) returns the InvAccum object, which is printed.
You can do most things to the Inventory objects using for_each( ). For example, for_each( ) can handily increase all the prices by 10%. But you'll notice that the Inventory objects have no way to change the item value. The programmers who designed Inventory thought this was a good idea. After all, why would you want to change the name of an item? But marketing has decided that they want a “new, improved” look by changing all the item names to uppercase. They've done studies and determined that the new names will boost sales (well, marketing needs to have something to do…). So for_each( ) will not work here, but transform( ) will:
//: C06:TransformNames.cpp
// More use of transform().
#include <algorithm>
#include <cctype>
#include <ctime>
#include <vector>
#include "Inventory.h"
#include "PrintSequence.h"
using namespace std;
struct NewImproved {
Inventory operator()(const Inventory& inv) {
return Inventory(toupper(inv.getItem()),
inv.getQuantity(), inv.getValue());
}
};
int main() {
vector<Inventory> vi;
srand(time(0)); // Randomize
generate_n(back_inserter(vi), 15,
InvenGen());
print(vi.begin(), vi.end(),
"vi");
transform(vi.begin(),vi.end(),vi.begin(),NewImproved());
print(vi.begin(), vi.end(),
"vi");
} ///:~Notice that the resulting range is the same as the input range; that is, the transformation is performed in place.
Now suppose that the sales department needs to generate special price lists with different discounts for each item. The original list must stay the same, and any number of special lists need to be generated. Sales will give you a separate list of discounts for each new list. To solve this problem, we can use the second version of transform( ):
//: C06:SpecialList.cpp
// Using the second version of transform().
#include <algorithm>
#include <ctime>
#include <vector>
#include "Inventory.h"
#include "PrintSequence.h"
using namespace std;
struct Discounter {
Inventory operator()(const Inventory& inv,
float discount) {
return Inventory(inv.getItem(), inv.getQuantity(),
int(inv.getValue() * (1 - discount)));
}
};
struct DiscGen {
float operator()() {
float r = float(rand() % 10);
return r / 100.0;
}
};
int main() {
vector<Inventory> vi;
srand(time(0)); // Randomize
generate_n(back_inserter(vi), 15, InvenGen());
print(vi.begin(), vi.end(), "vi");
vector<float> disc;
generate_n(back_inserter(disc), 15, DiscGen());
print(disc.begin(), disc.end(), "Discounts:");
vector<Inventory> discounted;
transform(vi.begin(),vi.end(), disc.begin(),
back_inserter(discounted), Discounter());
print(discounted.begin(),
discounted.end(),"discounted");
} ///:~Given an Inventory object and a discount percentage, the Discounter function object produces a new Inventory with the discounted price. The DiscGen function object just generates random discount values between 1% and 10% to use for testing. In main( ), two vectors are created, one for Inventory and one for discounts. These are passed to transform( ) along with a Discounter object, and transform( ) fills a new vector<Inventory> called discounted.
2-4-3-11. Numeric algorithms▲
These algorithms are all tucked into the header <numeric>, since they are primarily useful for performing numeric calculations.
T accumulate(InputIterator first, InputIterator last, T
result);
T accumulate(InputIterator first, InputIterator last, T
result, BinaryFunction f);
The first form is a generalized summation; for each element pointed to by an iterator i in [first, last), it performs the operation result = result + *i, where result is of type T. However, the second form is more general; it applies the function f(result, *i) on each element *i in the range from beginning to end.
Note the similarity between the second form of transform( ) and the second form of accumulate( ).
T inner_product(InputIterator1 first1, InputIterator1
last1, InputIterator2 first2, T init);
T inner_product(InputIterator1 first1, InputIterator1
last1, InputIterator2 first2, T init, BinaryFunction1
op1, BinaryFunction2 op2);
Calculates a generalized inner product of the two ranges [first1, last1) and [first2, first2 + (last1 - first1)). The return value is produced by multiplying the element from the first sequence by the “parallel” element in the second sequence and then adding it to the sum. Thus, if you have two sequences {1, 1, 2, 2} and {1, 2, 3, 4}, the inner product becomes
(1*1) + (1*2) + (2*3) + (2*4)which is 17. The init argument is the initial value for the inner product—this is probably zero but may be anything and is especially important for an empty first sequence, because then it becomes the default return value. The second sequence must have at least as many elements as the first.
The second form simply applies a pair of functions to its sequence. The op1 function is used in place of addition and op2 is used instead of multiplication. Thus, if you applied the second version of inner_product( ) to the sequence, the result would be the following operations:
init = op1(init, op2(1,1));
init = op1(init, op2(1,2));
init = op1(init, op2(2,3));
init = op1(init, op2(2,4));Thus, it's similar to transform( ), but two operations are performed instead of one.
OutputIterator partial_sum(InputIterator first,
InputIterator last, OutputIterator result);
OutputIterator partial_sum(InputIterator first,
InputIterator last, OutputIterator result,
BinaryFunction op);
Calculates a generalized partial sum. A new sequence is created, beginning at result. Each element is the sum of all the elements up to the currently selected element in [first, last). For example, if the original sequence is {1, 1, 2, 2, 3}, the generated sequence is {1, 1 + 1, 1 + 1 + 2, 1 + 1 + 2 + 2, 1 + 1 + 2 + 2 + 3}, that is, {1, 2, 4, 6, 9}.
In the second version, the binary function op is used instead of the + operator to take all the “summation” up to that point and combine it with the new value. For example, if you use multiplies<int>( ) as the object for the sequence, the output is {1, 1, 2, 4, 12}. Note that the first output value is always the same as the first input value.
The return value is the end of the output range [result, result + (last - first) ).
OutputIterator adjacent_difference(InputIterator first,
InputIterator last, OutputIterator result);
OutputIterator adjacent_difference(InputIterator first,
InputIterator last, OutputIterator result, BinaryFunction
op);
Calculates the differences of adjacent elements throughout the range [first, last). This means that in the new sequence, the value is the value of the difference of the current element and the previous element in the original sequence (the first value is unchanged). For example, if the original sequence is {1, 1, 2, 2, 3}, the resulting sequence is {1, 1 - 1, 2 - 1, 2 - 2, 3 - 2}, that is: {1, 0, 1, 0, 1}.
The second form uses the binary function op instead of the ‘-' operator to perform the “differencing.” For example, if you use multiplies<int>( ) as the function object for the sequence, the output is {1, 1, 2, 4, 6}.
The return value is the end of the output range [result, result + (last - first) ).
Example
This program tests all the algorithms in <numeric> in both forms, on integer arrays. You'll notice that in the test of the form where you supply the function or functions, the function objects used are the ones that produce the same result as form one, so the results will be exactly the same. This should also demonstrate a bit more clearly the operations that are going on and how to substitute your own operations.
//: C06:NumericTest.cpp
#include <algorithm>
#include <iostream>
#include <iterator>
#include <functional>
#include <numeric>
#include "PrintSequence.h"
using namespace std;
int main() {
int a[] = { 1, 1, 2, 2, 3, 5, 7, 9, 11, 13 };
const int ASZ = sizeof a / sizeof a[0];
print(a, a + ASZ, "a", " ");
int r = accumulate(a, a + ASZ, 0);
cout << "accumulate 1: " << r
<< endl;
// Should produce the same result:
r = accumulate(a, a + ASZ, 0, plus<int>());
cout << "accumulate 2: " << r
<< endl;
int b[] = { 1, 2, 3, 4, 1, 2, 3, 4, 1, 2 };
print(b, b + sizeof b / sizeof b[0], "b",
" ");
r = inner_product(a, a + ASZ, b, 0);
cout << "inner_product 1: " <<
r << endl;
// Should produce the same result:
r = inner_product(a, a + ASZ, b, 0,
plus<int>(), multiplies<int>());
cout << "inner_product 2: " <<
r << endl;
int* it = partial_sum(a, a + ASZ, b);
print(b, it, "partial_sum 1", "
");
// Should produce the same result:
it = partial_sum(a, a + ASZ, b, plus<int>());
print(b, it, "partial_sum 2", "
");
it = adjacent_difference(a, a + ASZ, b);
print(b, it, "adjacent_difference 1","
");
// Should produce the same result:
it = adjacent_difference(a, a + ASZ, b, minus<int>());
print(b, it, "adjacent_difference 2","
");
} ///:~Note that the return value of inner_product( ) and partial_sum( ) is the past-the-end iterator for the resulting sequence, so it is used as the second iterator in the print( ) function.
Since the second form of each function allows you to provide your own function object, only the first form of the function is purely “numeric.” You could conceivably do things that are not intuitively numeric with inner_product( ).
2-4-3-12. General utilities▲
Finally, here are some basic tools that are used with the other algorithms; you may or may not use them directly yourself.
(Templates in the <utility>
header)
template<class T1, class T2> struct pair;
template<class T1, class T2> pair<T1, T2>
make_pair(const T1&, const T2&);
These were described and used earlier in this chapter. A pair is simply a way to package two objects (which may be of different types) into a single object. This is typically used when you need to return more than one object from a function, but it can also be used to create a container that holds pair objects or to pass more than one object as a single argument. You access the elements by saying p.first and p.second, where p is the pair object. The function equal_range( ), described in this chapter, returns its result as a pair of iterators, for example. You can insert( ) a pair directly into a map or multimap; a pair is the value_type for those containers.
If you want to create a pair “on the fly,” you typically use the template function make_pair( ) rather than explicitly constructing a pair object. make_pair( ) deduces the types of the arguments it receives, relieving you of the typing as well as increasing robustness.
(From <iterator>)
difference_type distance(InputIterator first, InputIterator last);
Tells you the number of elements between first and last. More precisely, it returns an integral value that tells you the number of times first must be incremented before it is equal to last. No dereferencing of the iterators occurs during this process.
(From <iterator>)
Moves the iterator i forward by the value of n. (It can also be
moved backward for negative values of n if the iterator is
bidirectional.) This algorithm is aware of the different types of iterators and
will use the most efficient approach. For example, random iterators can be
incremented directly using ordinary arithmetic (i+=n), whereas a
bidirectional iterator must be incremented n times.
(From <iterator>)
back_insert_iterator<Container>
back_inserter(Container& x);
front_insert_iterator<Container>
front_inserter(Container& x);
insert_iterator<Container>
inserter(Container& x, Iterator i);
These functions are used to create iterators for the given containers that will insert elements into the container, rather than overwrite the existing elements in the container using operator= (which is the default behavior). Each type of iterator uses a different operation for insertion: back_insert_iterator uses push_back( ), front_insert_iterator uses push_front( ), and insert_iterator uses insert( ) (and thus it can be used with the associative containers, while the other two can be used with sequence containers). These will be shown in some detail in the next chapter.
const
LessThanComparable& min(const LessThanComparable& a,
const LessThanComparable& b);
const T& min(const T& a, const T& b,
BinaryPredicate binary_pred);
Returns the lesser of its two arguments, or returns the first argument if the two are equivalent. The first version performs comparisons using operator<, and the second passes both arguments to binary_pred to perform the comparison.
const
LessThanComparable& max(const LessThanComparable& a,
const LessThanComparable& b);
const T& max(const T& a, const T& b,
BinaryPredicate binary_pred);
Exactly like min( ), but returns the greater of its two arguments.
void swap(Assignable& a, Assignable& b);
void iter_swap(ForwardIterator1 a, ForwardIterator2 b);
Exchanges the values of a and b using assignment. Note that all container classes use specialized versions of swap( ) that are typically more efficient than this general version.
The iter_swap( ) function swaps the values that its two arguments reference.
2-4-4. Creating your own STL-style algorithms▲
Once you become comfortable with the style of STL algorithms, you can begin to create your own generic algorithms. Because these will conform to the conventions of all the other algorithms in the STL, they're easy to use for programmers who are familiar with the STL, and thus they become a way to “extend the STL vocabulary.”
The easiest way to approach the problem is to go to the <algorithm> header file, find something similar to what you need, and pattern your code after that.(98) (Virtually all STL implementations provide the code for the templates directly in the header files.)
If you take a close look at the list of algorithms in the Standard C++ library, you might notice a glaring omission: there is no copy_if( ) algorithm. Although it's true that you can accomplish the same effect with remove_copy_if( ), this is not quite as convenient because you have to invert the condition. (Remember, remove_copy_if( ) only copies those elements that don't match its predicate, in effect removing those that do.) You might be tempted to write a function object adaptor that negates its predicate before passing it to remove_copy_if( ), by including a statement something like this:
// Assumes pred is the incoming condition
replace_copy_if(begin, end, not1(pred));This seems reasonable, but when you remember that you want to be able to use predicates that are pointers to raw functions, you see why this won't work—not1 expects an adaptable function object. The only solution is to write a copy_if( ) algorithm from scratch. Since you know from inspecting the other copy algorithms that conceptually you need separate iterators for input and output, the following example will do the job:
//: C06:copy_if.h
// Create your own STL-style
algorithm.
#ifndef COPY_IF_H
#define COPY_IF_H
template<typename ForwardIter,
typename OutputIter, typename UnaryPred>
OutputIter copy_if(ForwardIter begin, ForwardIter end,
OutputIter dest, UnaryPred f) {
while(begin != end) {
if(f(*begin))
*dest++ = *begin;
++begin;
}
return dest;
}
#endif // COPY_IF_H ///:~Notice that the increment of begin cannot be integrated into the copy expression.
2-4-5. Summary▲
The goal of this chapter is to give you a practical understanding of the algorithms in the Standard Template Library. That is, to make you aware of and comfortable enough with the STL that you begin to use it on a regular basis (or, at least, to think of using it so you can come back here and hunt for the appropriate solution). The STL is powerful not only because it's a reasonably complete library of tools, but also because it provides a vocabulary for thinking about problem solutions and it is a framework for creating additional tools.
Although this chapter did show some examples of creating your own tools, we did not go into the full depth of the theory of the STL necessary to completely understand all the STL nooks and crannies. Such understanding will allow you to create tools more sophisticated than those shown here. This omission was in part because of space limitations, but mostly because it is beyond the charter of this book—our goal here is to give you practical understanding that will improve your day-to-day programming skills.
A number of books are dedicated solely to the STL (these are listed in the appendices), but we especially recommend Scott Meyers' Effective STL (Addison Wesley, 2002).
2-4-6. Exercises▲
Solutions to selected exercises can be found in the electronic document The Thinking in C++ Volume 2 Annotated Solution Guide, available for a small fee from www.MindView.net.
- Create a generator that returns the current value of clock( ) (in <ctime>). Create a list<clock_t>, and fill it with your generator using generate_n( ). Remove any duplicates in the list and print it to cout using copy( ).
- Using transform( ) and toupper( ) (in <cctype>), write a single function call that will convert a string to all uppercase letters.
- Create a Sum function object template that will accumulate all the values in a range when used with for_each( ).
- Write an anagram generator that takes a word as a command-line argument and produces all possible permutations of the letters.
- Write a “sentence anagram generator” that takes a sentence as a command-line argument and produces all possible permutations of the words in the sentence. (It leaves the words alone and just moves them around.)
- Create a class hierarchy with a base class B and a derived class D. Put a virtual member function void f( ) in B such that it will print a message indicating that B's f( ) was called, and redefine this function for D to print a different message. Create a vector<B*>, and fill it with B and D objects. Use for_each( ) to call f( ) for each of the objects in your vector.
- Modify FunctionObjects.cpp so that it uses float instead of int.
- Modify FunctionObjects.cpp so that it templatizes the main body of tests so you can choose which type you're going to test. (You'll have to pull most of main( ) out into a separate template function.)
- Write a program that takes an integer as a command line argument and finds all of its factors.
- Write a program that takes as a command-line argument the name of a text file. Open this file and read it a word at a time (hint: use >>). Store each word into a vector<string>. Force all the words to lowercase, sort them, remove all the duplicates, and print the results.
- Write a program that finds all the words that are in common between two input files, using set_intersection( ). Change it to show the words that are not in common, using set_symmetric_difference( ).
- Create a program that, given an integer on the command line, creates a “factorial table” of all the factorials up to and including the number on the command line. To do this, write a generator to fill a vector<int>, and then use partial_sum( ) with a standard function object.
- Modify CalcInventory.cpp so that it will find all the objects that have a quantity that's less than a certain amount. Provide this amount as a command-line argument, and use copy_if( ) and bind2nd( ) to create the collection of values less than the target value.
- Use UrandGen( ) to generate 100 numbers. (The size of the numbers does not matter.) Find which numbers in your range are congruent mod 23 (meaning they have the same remainder when divided by 23). Manually pick a random number yourself, and determine whether that number is in your range by dividing each number in the list by your number and checking if the result is 1 instead of just using find( ) with your value.
- Fill a vector<double> with numbers representing angles in radians. Using function object composition, take the sine of all the elements in your vector (see <cmath>).
- Test the speed of your computer. Call srand(time(0)), then make an array of random numbers. Call srand(time(0)) again and generate the same number of random numbers in a second array. Use equal( ) to see if the arrays are the same. (If your computer is fast enough, time(0) will return the same value both times it is called.) If the arrays are not the same, sort them and use mismatch( ) to see where they differ. If they are the same, increase the length of your array and try again.
- Create an STL-style algorithm transform_if( ) following the first form of transform( ) that performs transformations only on objects that satisfy a unary predicate. Objects that don't satisfy the predicate are omitted from the result. It needs to return a new “end” iterator.
- Create an STL-style algorithm that is an overloaded version of for_each( ) which follows the second form of transform( ) and takes two input ranges so it can pass the objects of the second input range a to a binary function that it applies to each object of the first range.
- Create a Matrix class template that is made from a vector<vector<T> >. Provide it with a friend ostream& operator<<(ostream&, const Matrix&) to display the matrix. Create the following binary operations using the STL function objects where possible: operator+(const Matrix&, const Matrix&) for matrix addition, operator*(const Matrix&, const vector<int>&) for multiplying a matrix by a vector, and operator*(const Matrix&, const Matrix&) for matrix multiplication. (You might need to look up the mathematical meanings of the matrix operations if you don't remember them.) Test your Matrix class template using int and float.
- Using the characters
"~`!@#$%^&*( )_-+=}{[]|\:;"'<.>,?/",
generate a codebook using an input file given on the command line as a dictionary of words. Don't worry about stripping off the non-alphabetic characters nor worry about case of the words in the dictionary file. Map each permutation of the character string to a word such as the following:
"=')/%[}]|{*@?!"`,;>&^-~_:$+.#(<\" apple
"|]\~>#.+%(/-_[`':;=}{*"$^!&?),@<" carrot
"@=~['].\/<-`>#*)^%+,";&?!_{:|$}(" Carrot
etc.
Make sure that no duplicate codes or words exist in your code book. Use lexicographical_compare( ) to perform a sort on the codes. Use your code book to encode the dictionary file. Decode your encoding of the dictionary file, and make sure you get the same contents back. - Using the following names:
Jon Brittle
Jane Brittle
Mike Brittle
Sharon Brittle
George Jensen
Evelyn Jensen
Find all the possible ways to arrange them for a wedding picture.
- After being separated for one picture, the bride and groom decided they wanted to be together for all of them. Find all the possible ways to arrange the people for the picture if the bride and groom (Jon Brittle and Jane Brittle) are to be next to each other.
- A travel company wants to find out the average number of days
people take to travel from one end of the continent to another. The problem is
that in the survey, some people did not take a direct route and took much
longer than is needed (such unusual data points are called “outliers”). Using
the following generator, generate travel days into a vector. Use remove_if( )
to remove all the outliers in your vector. Take the average of the data
in the vector to find out how long people generally take to travel.
Sélectionnez
inttravelTime(){// The "outlier"if(rand()%10==0)returnrand()%100;// Regular routereturnrand()%10+10;} - Determine how much faster binary_search( ) is to find( ) when it comes to searching sorted ranges.
- The army wants to recruit people from its selective service list. They have decided to recruit those that signed up for the service in 1997 starting from the oldest down to the youngest. Generate an arbitrary amount of people (give them data members such as age and yearEnrolled) into a vector. Partition the vector so that those who enrolled in 1997 are ordered at the beginning of the list, starting from the youngest to the oldest, and leave the remaining part of the list sorted according to age.
- Make a class called Town with population, altitude, and weather data members. Make the weather an enum with { RAINY, SNOWY, CLOUDY, CLEAR }. Make a class that generates Town objects. Generate town names (whether they make sense or not it doesn't matter) or pull them off the Internet. Ensure that the whole town name is lower case and there are no duplicate names. For simplicity, we recommend keeping your town names to one word. For the population, altitudes, and weather fields, make a generator that will randomly generate weather conditions, populations within the range [100 to 1,000,000) and altitudes between [0, 8000) feet. Fill a vector with your Town objects. Rewrite the vector out to a new file called Towns.txt.
- There was a baby boom, resulting in a 10% population increase in every town. Update your town data using transform( ), rewrite your data back out to file.
- Find the towns with the highest and lowest population. For this exercise, implement operator< for your Town class. Also try implementing a function that returns true if its first parameter is less than its second. Use it as a predicate to call the algorithm you use.
- Find all the towns within the altitudes 2500-3500 feet inclusive. Implement equality operators for the Town class as needed.
- We need to place an airport in a certain altitude, but location is not a problem. Organize your list of towns so that there are no duplicate (duplicate meaning that no two altitudes are within the same 100 ft range. Such classes would include [100, 199), [200, 199), etc. altitudes. Sort this list in ascending order in at least two different ways using the function objects in <functional>. Do the same for descending order. Implement relational operators for Town as needed.
- Generate an arbitrary number of random numbers in a stack-based array. Use max_element( ) to find the largest number in array. Swap it with the number at the end of your array. Find the next largest number and place it in the array in the position before the previous number. Continue doing this until all elements have been moved. When the algorithm is complete, you will have a sorted array. (This is a “selection sort”.)
- Write a program that will take phone numbers from a file (that
also contains names and other suitable information) and change the numbers that
begin with 222 to 863. Be sure to save the old numbers. The file format is as
follows:
222 8945
756 3920
222 8432
etc.
- Write a program that, given a last name, will find everyone with
that last name with his or her corresponding phone number. Use the algorithms
that deal with ranges (lower_bound, upper_bound, equal_range,
etc.). Sort with the last name acting as a primary key and the first name
acting as a secondary key. Assume that you will read the names and numbers from
a file where the format will be as follows. (Be sure to order them so that the
last names are ordered, and the first names are ordered within the last
names.):
John Doe 345 9483
Nick Bonham 349 2930
Jane Doe 283 2819
- Given a file with data similar to the following, pull all the
state acronyms from the file and put them in a separate file. (Note that you
can't depend on the line number for the type of data. The data is on random
lines.)
ALABAMA
AL
AK
ALASKA
ARIZONA
AZ
ARKANSAS
AR
CA
CALIFORNIA
CO
COLORADO
etc.
When complete, you should have a file with all the state acronyms which are:
AL AK AZ AR CA CO CT DE FL GA HI ID IL IN IA KS KY LA ME MD MA MI MN MS MO MT NE NV NH NJ NM NY NC ND OH OK OR PA RI SC SD TN TX UT VT VA WA WV WI WY
- Make an Employee class with two data members: hours and hourlyPay. Employee shall also have a calcSalary( ) function which returns the pay for that employee. Generate random hourly pay and hours for an arbitrary amount of employees. Keep a vector<Employee*>. Find out how much money the company is going to spend for this pay period.
- Race sort( ), partial_sort( ),and nth_element( ) against each other and find out if it's really worth the time saved to use one of the weaker sorts if they're all that's needed.
2-5. Generic Containers▲
Container classes are the solution to a specific kind of code reuse problem. They are building blocks used to create object-oriented programs, and they make the internals of a program much easier to construct.
A container class describes an object that holds other objects. Container classes are so important that they were considered fundamental to early object-oriented languages. In Smalltalk, for example, programmers think of the language as the program translator together with the class library, and a critical part of that library is the set of container classes. It became natural, therefore, for C++ compiler vendors to also include a container class library. You'll note that the vector is so useful that it was introduced in its simplest form early in Volume 1 of this book.
Like many other early C++ libraries, early container class libraries followed Smalltalk's object-based hierarchy, which worked well for Smalltalk, but turned out to be awkward and difficult to use in C++. Another approach was required.
The C++ approach to containers is based on templates. The containers in the Standard C++ library represent a broad range of data structures designed to work well with the standard algorithms and to meet common software development needs.
2-5-1. Containers and iterators▲
If you don't know how many objects you're going to need to solve a particular problem, or how long they will last, you also don't know ahead of time how to store those objects. How can you know how much space to create? The answer is you don't—until run time.
The solution to most problems in object-oriented design seems simple; you create another type of object. For the storage problem, the new type of object holds other objects or pointers to objects. This new type of object, which is typically referred to in C++ as a container (also called a collection in some languages), expands itself whenever necessary to accommodate everything you place inside it. You don't need to know ahead of time how many objects you're going to place in a container; you just create a container object and let it take care of the details.
Fortunately, a good object-oriented programming language comes with a set of containers. In C++, it's the Standard Template Library (STL). In some libraries, a generic container is considered good enough for all needs, and in others (C++ in particular) the library has different types of containers for different needs: a vector for efficient access to all elements, and a linked list for efficient insertion at all positions, and several more, so you can choose the particular type that fits your needs.
All containers have some way to put things in and get things out. The way you place something into a container is fairly obvious; there's a function called “push” or “add” or a similar name. The way you retrieve things from a container is not always as apparent; if an entity is array-like, such as a vector, you might be able to use an indexing operator or function. But in many situations this doesn't make sense. Also, a single-selection function is restrictive. What if you want to manipulate or compare a group of elements in the container?
The solution for flexible element access is the iterator, an object whose job is to select the elements within a container and present them to the user of the iterator. As a class, an iterator also provides a level of abstraction, which you can use to separate the details of the container from the code that's accessing that container. The container, via the iterator, is seen as a sequence. The iterator lets you traverse the sequence without worrying about the underlying structure—that is, whether it's a vector, a linked list, a set, or something else. This gives you the flexibility to easily change the underlying data structure without disturbing the code in your program that traverses the container. Separating iteration from the container's control also allows multiple simultaneous iterators.
From a design standpoint, all you really want is a sequence that can be manipulated to solve your problem. If a single type of sequence satisfied all your needs, there would be no reason to have different types. You need a choice of containers for two reasons. First, containers provide different types of interfaces and external behavior. A stack has an interface and a behavior that is different from that of a queue, which is different from that of a set or a list. One of these might provide a more flexible solution to your problem than the other, or it might provide a clearer abstraction that conveys your design intent. Second, different containers have different efficiencies for certain operations. Compare a vector to a list, for example. Both are simple sequences that can have nearly identical interfaces and external behaviors. But certain operations can have radically different costs. Randomly accessing elements in a vector is a constant-time operation; it takes the same amount of time regardless of the element you select. However, it is expensive to move through a linked list to randomly access an element, and it takes longer to find an element if it is farther down the list. On the other hand, if you want to insert an element in the middle of a sequence, it's cheaper with a list than with a vector. The efficiencies of these and other operations depend on the underlying structure of the sequence. In the design phase, you might start with a list and, when tuning for performance, change to a vector, or vice-versa. Because of iterators, code that merely traverses sequences is insulated from changes in the underlying sequence implementation.
Remember that a container is only a storage cabinet that holds objects. If that cabinet solves all your needs, it probably doesn't really matter how it is implemented. If you're working in a programming environment that has built-in overhead due to other factors, the cost difference between a vector and a linked list might not matter. You might need only one type of sequence. You can even imagine the “perfect” container abstraction, which can automatically change its underlying implementation according to the way it is used.(99)
2-5-1-1. STL reference documentation▲
As in the previous chapter, you will notice that this chapter does not contain exhaustive documentation describing each of the member functions in each STL container. Although we describe the member functions we use, we've left the full descriptions to others. We recommend the online resources available for the Dinkumware, Silicon Graphics, and STLPort STL implementations.(100)
2-5-2. A first look▲
Here's an example using the set class template, a container modeled after a traditional mathematical set and which does not accept duplicate values. The following set was created to work with ints:
//: C07:Intset.cpp
// Simple use of STL set.
#include <cassert>
#include <set>
using namespace std;
int main() {
set<int> intset;
for(int i = 0; i < 25; i++)
for(int j = 0; j < 10; j++)
// Try to insert duplicates:
intset.insert(j);
assert(intset.size() == 10);
} ///:~The insert( ) member does all the work: it attempts to insert an element and ignores it if it's already there. Often the only activities involved in using a set are simply insertion and testing to see whether it contains the element. You can also form a union, an intersection, or a difference of sets and test to see if one set is a subset of another. In this example, the values 0-9 are inserted into the set 25 times, but only the 10 unique instances are accepted.
Now consider taking the form of Intset.cpp and modifying it to display a list of the words used in a document. The solution becomes remarkably simple.
//: C07:WordSet.cpp
#include <fstream>
#include <iostream>
#include <iterator>
#include <set>
#include <string>
#include "../require.h"
using namespace std;
void wordSet(const char* fileName) {
ifstream source(fileName);
assure(source, fileName);
string word;
set<string> words;
while(source >> word)
words.insert(word);
copy(words.begin(), words.end(),
ostream_iterator<string>(cout,
"\n"));
cout << "Number of unique words:"
<< words.size() << endl;
}
int main(int argc, char* argv[]) {
if(argc > 1)
wordSet(argv[1]);
else
wordSet("WordSet.cpp");
} ///:~The only substantive difference here is that the set holds strings instead of integers. The words are pulled from a file, but the other operations are similar to those in Intset.cpp. Not only does the output reveal that duplicates have been ignored, but because of the way set is implemented, the words are automatically sorted.
A set is an example of an associative container, one of the three categories of containers provided by the Standard C++ library. The containers and their categories are summarized in the following table:
| Category | Containers |
| Sequence Containers | vector, list, deque |
| Container Adaptors | queue, stack, priority_queue |
| Associative Containers | set, map, multiset, multimap |
These categories represent different models that are used for different needs. The Sequence Containers simply organize their elements linearly, and are the most fundamental type of containers. For some problems, special properties need to be attached to these sequences, and that's exactly what the Container Adaptors do—they model abstractions such as a queue or stack. The associative containers organize their data based on keys, allowing for fast retrieval of that data.
All the containers in the standard library hold copies of the objects you place in them, and expand their resources as needed, so your objects must be copy-constructible (have an accessible copy constructor) and assignable (have an accessible assignment operator). The key difference between one container and another is the way the objects are stored in memory and what operations are available to the user.
A vector, as you already know, is a linear sequence that allows rapid random access to its elements. However, it's expensive to insert an element in the middle of a co-located sequence like a vector, just as it is with an array. A deque (double-ended-queue, pronounced “deck”) also allows random access that's nearly as fast as vector, but it's significantly faster when it needs to allocate new storage, and you can easily add new elements at the front as well as the back of the sequence. A list is a doubly linked list, so it's expensive to move around randomly but cheap to insert an element anywhere. Thus list, deque and vector are similar in their basic functionality (they all hold linear sequences), but different in the cost of their activities. For your first attempt at a program, you could choose any one and experiment with the others only if you're tuning for efficiency.
Many of the problems you set out to solve will only require a simple linear sequence such as a vector, deque, or list. All three have a member function push_back( ) that you use to insert a new element at the back of the sequence (deque and list also have push_front( ), which inserts elements at the beginning of the sequence).
But how do you retrieve the elements stored in a sequence container? With a vector or deque, it is possible to use the indexing operator[ ], but that doesn't work with list. You can use iterators on all three sequences to access elements. Each container provides the appropriate type of iterator for accessing its elements.
Even though the containers hold objects by value (that is, they hold copies of whole objects), sometimes you'll want to store pointers so that you can refer to objects from a hierarchy and thus take advantage of the polymorphic behavior of the classes represented. Consider the classic “shape” example where shapes have a set of common operations, and you have different types of shapes. Here's what it looks like using the STL vector to hold pointers to various Shape types created on the heap:
//: C07:Stlshape.cpp
// Simple shapes using the STL.
#include <vector>
#include <iostream>
using namespace std;
class Shape {
public:
virtual void draw() = 0;
virtual ~Shape() {};
};
class Circle : public Shape {
public:
void draw() { cout << "Circle::draw”
<< endl; }
~Circle() { cout << "~Circle” <<
endl; }
};
class Triangle : public Shape {
public:
void draw() { cout << "Triangle::draw”
<< endl; }
~Triangle() { cout << "~Triangle” <<
endl; }
};
class Square : public Shape {
public:
void draw() { cout << "Square::draw”
<< endl; }
~Square() { cout << "~Square” <<
endl; }
};
int main() {
typedef std::vector<Shape*> Container;
typedef Container::iterator Iter;
Container shapes;
shapes.push_back(new Circle);
shapes.push_back(new Square);
shapes.push_back(new Triangle);
for(Iter i = shapes.begin(); i != shapes.end(); i++)
(*i)->draw();
// ... Sometime later:
for(Iter j = shapes.begin(); j != shapes.end(); j++)
delete *j;
} ///:~The creation of Shape, Circle, Square, and Triangle should be fairly familiar. Shape is an abstract base class (because of the pure specifier =0) that defines the interface for all types of Shapes. The derived classes override the virtual function draw( ) to perform the appropriate operation. Now we'd like to create a bunch of different types of Shape objects, and the natural place to store them is in an STL container. For convenience, this typedef:
typedef std::vector<Shape*> Container;creates an alias for a vector of Shape*, and this typedef:
typedef Container::iterator Iter;uses that alias to create another one, for vector<Shape*>::iterator. Notice that the container type name must be used to produce the appropriate iterator, which is defined as a nested class. Although there are different types of iterators (forward, bidirectional, random, and so on), they all have the same basic interface: you can increment them with ++, you can dereference them to produce the object they're currently selecting, and you can test them to see if they're at the end of the sequence. That's what you'll want to do 90 percent of the time. And that's what is done in the previous example: after a container is created, it's filled with different types of Shape pointers. Notice that the upcast happens as the Circle, Square, or Rectangle pointer is added to the Shapes container, which doesn't know about those specific types but instead holds only Shape*. As soon as the pointer is added to the container, it loses its specific identity and becomes an anonymous Shape*. This is exactly what we want: toss them all in and let polymorphism sort it out.
The first for loop creates an iterator and sets it to the beginning of the sequence by calling the begin( ) member function for the container. All containers have begin( ) and end( ) member functions that produce an iterator selecting, respectively, the beginning of the sequence and one past the end of the sequence. To test to see if you're done, you make sure the iterator is not equal to the iterator produced by end( ); don't use < or <=. The only tests that work are != and ==, so it's common to write a loop like:
for(Iter i = shapes.begin(); i != shapes.end(); i++)This says “take me through every element in the sequence.”
What do you do with the iterator to produce the element it's selecting? You dereference it using (what else?) the ‘*' (which is actually an overloaded operator). What you get back is whatever the container is holding. This container holds Shape*, so that's what *i produces. If you want to call a Shape member function, you must do so with the -> operator, so you write the line:
(*i)->draw();This calls the draw( ) function for the Shape* the iterator is currently selecting. The parentheses are ugly but necessary to produce the desired operator precedence.
As they are destroyed or in other cases where the pointers are removed, the STL containers do not automatically call delete for the pointers they contain. If you create an object on the heap with new and place its pointer in a container, the container can't tell if that pointer is also placed inside another container, nor if it refers to heap memory in the first place. As always, you are responsible for managing your own heap allocations. The last lines in the program move through and delete every object in the container so that proper cleanup occurs. The easiest and safest way to handle pointers in containers is to use smart pointers. It should be noted that auto_ptr can't be used for this purpose, so you will need to look outside of the C++ Standard Library for a suitable smart pointers.(101)
You can change the type of container that this program uses with two lines. Instead of including <vector>, you include <list>, and in the first typedef you say:
typedef std::list<Shape*> Container;instead of using a vector. Everything else goes untouched. This is possible not because of an interface enforced by inheritance (there is little inheritance in the STL), but because the interface is enforced by a convention adopted by the designers of the STL, precisely so you could perform this kind of interchange. Now you can easily switch between vector and list or any other container that supports the same interface (both syntactically and semantically) and see which one works fastest for your needs.
2-5-2-1. Containers of strings▲
In the previous example, at the end of main( ) it was necessary to move through the whole list and delete all the Shape pointers:
for(Iter j = shapes.begin(); j != shapes.end(); j++)
delete *j;STL containers make sure that each object they contain has its destructor called when the container itself is destroyed. Pointers, however, have no destructor, so we have to delete them ourselves.
This highlights what could be seen as an oversight in the STL: there's no facility in any of the STL containers to automatically delete the pointers they contain, so you must do it manually. It's as if the assumption of the STL designers was that containers of pointers weren't an interesting problem, but that's not the case.
Automatically deleting a pointer turns out to be problematic because of the multiple membership problem. If a container holds a pointer to an object, it's not unlikely that pointer could also be in another container. A pointer to an Aluminum object in a list of Trash pointers could also reside in a list of Aluminum pointers. If that happens, which list is responsible for cleaning up that object—that is, which list “owns” the object?
This question is virtually eliminated if the object rather than a pointer resides in the list. Then it seems clear that when the list is destroyed, the objects it contains must also be destroyed. Here, the STL shines, as you can see when creating a container of string objects. The following example stores each incoming line as a string in a vector<string>:
//: C07:StringVector.cpp
// A vector of strings.
#include <fstream>
#include <iostream>
#include <iterator>
#include <sstream>
#include <string>
#include <vector>
#include "../require.h"
using namespace std;
int main(int argc, char* argv[]) {
const char* fname = "StringVector.cpp";
if(argc > 1) fname = argv[1];
ifstream in(fname);
assure(in, fname);
vector<string> strings;
string line;
while(getline(in, line))
strings.push_back(line);
// Do something to the strings...
int i = 1;
vector<string>::iterator w;
for(w = strings.begin(); w !=
strings.end(); w++) {
ostringstream ss;
ss << i++;
*w = ss.str() + ": " + *w;
}
// Now send them out:
copy(strings.begin(), strings.end(),
ostream_iterator<string>(cout,
"\n"));
// Since they aren't pointers, string
// objects clean themselves up!
} ///:~Once the vector<string> called strings is created, each line in the file is read into a string and put in the vector:
while(getline(in, line))
strings.push_back(line);The operation that's being performed on this file is to add line numbers. A stringstream provides easy conversion from an int to a string of characters representing that int.
Assembling string objects is quite easy, since operator+ is overloaded. Sensibly enough, the iterator w can be dereferenced to produce a string that can be used as both an rvalue and an lvalue:
*w = ss.str() + ": " + *w;You may be surprised that you can assign back into the container via the iterator, but it's a tribute to the careful design of the STL.
Because the vector<string> contains the objects, two things are worthy of note. First, as explained before, you don't need to explicitly clean up the string objects. Even if you put addresses of the string objects as pointers into other containers, it's clear that strings is the “master list” and maintains ownership of the objects.
Second, you are effectively using dynamic object creation, and yet you never use new or delete! It's all taken care of for you by the vector because it stores copies of the objects you give it. Thus your coding is significantly cleaned up.
2-5-2-2. Inheriting from STL containers▲
The power of instantly creating a sequence of elements is amazing, and it makes you realize how much time you may have lost in the past solving this particular problem. For example, many utility programs involve reading a file into memory, modifying the file, and writing it back out to disk. You might as well take the functionality in StringVector.cpp and package it into a class for later reuse.
Now the question is: do you create a member object of type vector, or do you inherit? A general object-oriented design guideline is to prefer composition (member objects) over inheritance, but the standard algorithms expect sequences that implement a particular interface, so inheritance is often necessary.
//: C07:FileEditor.h
// A file editor tool.
#ifndef FILEEDITOR_H
#define FILEEDITOR_H
#include <iostream>
#include <string>
#include <vector>
class FileEditor : public
std::vector<std::string> {
public:
void open(const char* filename);
FileEditor(const char* filename) { open(filename); }
FileEditor() {};
void write(std::ostream& out = std::cout);
};
#endif // FILEEDITOR_H ///:~The constructor opens the file and reads it into the FileEditor, and write( ) puts the vector of string onto any ostream. Notice in write( ) that you can have a default argument for the reference.
The implementation is quite simple:
//: C07:FileEditor.cpp {O}
#include "FileEditor.h"
#include <fstream>
#include "../require.h"
using namespace std;
void FileEditor::open(const char* filename) {
ifstream in(filename);
assure(in, filename);
string line;
while(getline(in, line))
push_back(line);
}
// Could also use copy() here:
void FileEditor::write(ostream& out) {
for(iterator w = begin(); w != end(); w++)
out << *w << endl;
} ///:~The functions from StringVector.cpp are simply repackaged. Often this is the way classes evolve—you start by creating a program to solve a particular application and then discover some commonly used functionality within the program that can be turned into a class.
The line-numbering program can now be rewritten using FileEditor:
//: C07:FEditTest.cpp
//{L} FileEditor
// Test the FileEditor tool.
#include <sstream>
#include "FileEditor.h"
#include "../require.h"
using namespace std;
int main(int argc, char* argv[]) {
FileEditor file;
if(argc > 1) {
file.open(argv[1]);
} else {
file.open("FEditTest.cpp");
}
// Do something to the lines...
int i = 1;
FileEditor::iterator w = file.begin();
while(w != file.end()) {
ostringstream ss;
ss << i++;
*w = ss.str() + ": " + *w;
++w;
}
// Now send them to cout:
file.write();
} ///:~Now the operation of reading the file is in the constructor:
FileEditor file(argv[1]);(or in the open( ) member function), and writing happens in the single line (which defaults to sending the output to cout):
file.write();The bulk of the program is involved with modifying the file in memory.
2-5-3. A plethora of iterators▲
An iterator is an abstraction for genericity. It works with different types of containers without knowing the underlying structure of those containers. Most containers support iterators,(102) so you can say:
<ContainerType>::iterator
<ContainerType>::const_iteratorto produce the iterator types for a container. Every container has a begin( ) member function that produces an iterator indicating the beginning of the elements in the container, and an end( ) member function that produces an iterator which is the past-the-endmarker of the container. If the container is const¸ begin( ) and end( ) produce const iterators, which disallow changing the elements pointed to (because the appropriate operators are const).
All iterators can advance within their sequence (via operator++) and allow == and != comparisons. Thus, to move an iterator it forward without running it off the end, you say something like:
while(it != pastEnd) {
// Do something
++it;
}where pastEnd is the past-the-end marker produced by the container's end( ) member function.
An iterator can be used to produce the container element that it is currently selecting via the dereferencing operator (operator*). This can take two forms. If it is an iterator traversing a container, and f( ) is a member function of the type of objects held in the container, you can say either:
(*it).f();or
it->f();Knowing this, you can create a template that works with any container. Here, the apply( ) function template calls a member function for every object in the container, using a pointer to member that is passed as an argument:
//: C07:Apply.cpp
// Using simple iteration.
#include <iostream>
#include <vector>
#include <iterator>
using namespace std;
template<class Cont, class PtrMemFun>
void apply(Cont& c, PtrMemFun f) {
typename Cont::iterator it = c.begin();
while(it != c.end()) {
((*it).*f)(); // Alternate form
++it;
}
}
class Z {
int i;
public:
Z(int ii) : i(ii) {}
void g() { ++i; }
friend ostream& operator<<(ostream& os,
const Z& z) {
return os << z.i;
}
};
int main() {
ostream_iterator<Z> out(cout, " ");
vector<Z> vz;
for(int i = 0; i < 10; i++)
vz.push_back(Z(i));
copy(vz.begin(), vz.end(), out);
cout << endl;
apply(vz, &Z::g);
copy(vz.begin(), vz.end(), out);
} ///:~You can't use operator-> here because the resulting statement would be:
(it->*f)();which attempts to use the iterator's operator->*, which is not provided by the iterator classes.(103)
It is much easier to use either for_each( ) or transform( ) to apply functions to sequences, as you saw in the previous chapter.
2-5-3-1. Iterators in reversible containers▲
A container may also be reversible, which means that it can produce iterators that move backward from the end, as well as iterators that move forward from the beginning. All standard containers support such bidirectional iteration.
A reversible container has the member functions rbegin( ) (to produce a reverse_iterator selecting the end) and rend( ) (to produce a reverse_iterator indicating “one past the beginning”). If the container is const, rbegin( ) and rend( ) will produce const_reverse_iterators.
The following example uses vector but will work with all containers that support iteration:
//: C07:Reversible.cpp
// Using reversible containers.
#include <fstream>
#include <iostream>
#include <string>
#include <vector>
#include "../require.h"
using namespace std;
int main() {
ifstream in("Reversible.cpp");
assure(in, "Reversible.cpp");
string line;
vector<string> lines;
while(getline(in, line))
lines.push_back(line);
for(vector<string>::reverse_iterator r =
lines.rbegin();
r != lines.rend(); r++)
cout << *r << endl;
} ///:~You move backward through the container using the same syntax as you do when moving forward through a container with an ordinary iterator.
2-5-3-2. Iterator categories▲
The iterators in the Standard C++ library are classified into “categories” that describe their capabilities. The order in which they are generally described moves from the categories with the most restricted behavior to those with the most powerful behavior.
Input: read-only, one pass
The only predefined implementations of input iterators are istream_iterator and istreambuf_iterator, to read from an istream. As you can imagine, an input iterator can only be dereferenced once for each element that's selected, just as you can only read a particular portion of an input stream once. They can only move forward. A special constructor defines the past-the-end value. In summary, you can dereference it for reading (once only for each value) and move it forward.
Output: write-only, one pass
This is the complement of an input iterator, but for writing rather than reading. The only predefined implementations of output iterators are ostream_iterator and ostreambuf_iterator, to write to an ostream, and the less commonly used raw_storage_iterator. Again, these can only be dereferenced once for each written value, and they can only move forward. There is no concept of a terminal past-the-end value for an output iterator. Summarizing, you can dereference it for writing (once only for each value) and move it forward.
Forward: multiple read/write
The forward iterator contains all the functionality of both the input iterator and the output iterator, plus you can dereference an iterator location multiple times, so you can read and write to a value multiple times. As the name implies, you can only move forward. There are no predefined iterators that are only forward iterators.
Bidirectional: operator--
The bidirectional iterator has all the functionality of the forward iterator, and in addition it can be moved backward one location at a time using operator--. The iterators returned by the list container are bidirectional.
Random-access: like a pointer
Finally, the random-access iterator has all the functionality of the bidirectional iterator plus all the functionality of a pointer (a pointer is a random-access iterator), except that there is no “null” iterator analogue to a null pointer. Basically, anything you can do with a pointer you can do with a random-access iterator, including indexing with operator[ ], adding integral values to a pointer to move it forward or backward by a number of locations, or comparing one iterator to another with comparison operators.
Is this really important?
Why do you care about this categorization? When you're just using containers in a straightforward way (for example, just hand-coding all the operations you want to perform on the objects in the container), it usually doesn't matter. Things either work or they don't. The iterator categories become important when:
- You use some of the fancier built-in iterator types that will be demonstrated shortly, or you “graduate” to creating your own iterators (demonstrated later in this chapter).
- You use the STL algorithms (the subject of the previous chapter). Each of the algorithms places requirements on its iterators. Knowledge of the iterator categories is even more important when you create your own reusable algorithm templates, because the iterator category required by your algorithm determines how flexible the algorithm will be. If you require only the most primitive iterator category (input or output), your algorithm will work with everything (copy( ) is an example of this).
An iterator's category is identified by a hierarchy of iterator tag classes. The class names correspond to the iterator categories, and their derivation reflects the relationship between them:
struct input_iterator_tag {};
struct output_iterator_tag {};
struct forward_iterator_tag :
public input_iterator_tag {};
struct bidirectional_iterator_tag :
public forward_iterator_tag {};
struct random_access_iterator_tag :
public bidirectional_iterator_tag {};The class forward_iterator_tag derives only from input_iterator_tag, not from output_iterator_tag, because we need to have past-the-end iterator values in algorithms that use forward iterators, but algorithms that use output iterators always assume that operator* can be dereferenced. For this reason, it is important to make sure that a past-the-end value is never passed to an algorithm that expects an output iterator.
For efficiency, certain algorithms provide different implementations for different iterator types, which they infer from the iterator tag defined by the iterator. We will use some of these tag classes later in this chapter when we define our own iterator types.
2-5-3-3. Predefined iterators▲
The STL has a predefined set of iterators that can be quite handy. For example, you've already seen the reverse_iterator objects produced by calling rbegin( ) and rend( ) for all the basic containers.
The insertion iterators are necessary because some of the STL algorithms—copy( ), for example—use the assignment operator= to place objects in the destination container. This is a problem when you're using the algorithm to fill the container rather than to overwrite items that are already in the destination container—that is, when the space isn't already there. What the insert iterators do is change the implementation of operator= so that instead of doing an assignment, it calls a “push” or “insert” function for that container, thus causing it to allocate new space. The constructors for both back_insert_iterator and front_insert_iterator take a basic sequence container object (vector, deque or list) as their argument and produce an iterator that calls push_back( ) or push_front( ), respectively, to perform assignment. The helper functions back_inserter( ) and front_inserter( ) produce these insert-iterator objects with a little less typing. Since all the basic sequence containers support push_back( ), you will probably find yourself using back_inserter( ) with some regularity.
An insert_iterator lets you insert elements in the middle of the sequence, again replacing the meaning of operator=, but this time by automatically calling insert( ) instead of one of the “push” functions. The insert( ) member function requires an iterator indicating the place to insert before, so the insert_iterator requires this iterator in addition to the container object. The shorthand function inserter( ) produces the same object.
The following example shows the use of the different types of inserters:
//: C07:Inserters.cpp
// Different types of iterator inserters.
#include <iostream>
#include <vector>
#include <deque>
#include <list>
#include <iterator>
using namespace std;
int a[] = { 1, 3, 5, 7, 11, 13, 17, 19, 23 };
template<class Cont> void
frontInsertion(Cont& ci) {
copy(a, a + sizeof(a)/sizeof(Cont::value_type),
front_inserter(ci));
copy(ci.begin(), ci.end(),
ostream_iterator<typename Cont::value_type>(
cout, " "));
cout << endl;
}
template<class Cont> void backInsertion(Cont&
ci) {
copy(a, a + sizeof(a)/sizeof(Cont::value_type),
back_inserter(ci));
copy(ci.begin(), ci.end(),
ostream_iterator<typename Cont::value_type>(
cout, " "));
cout << endl;
}
template<class Cont> void midInsertion(Cont&
ci) {
typename Cont::iterator it = ci.begin();
++it; ++it; ++it;
copy(a, a + sizeof(a)/(sizeof(Cont::value_type) * 2),
inserter(ci, it));
copy(ci.begin(), ci.end(),
ostream_iterator<typename Cont::value_type>(
cout, " "));
cout << endl;
}
int main() {
deque<int> di;
list<int> li;
vector<int> vi;
// Can't use a front_inserter() with vector
frontInsertion(di);
frontInsertion(li);
di.clear();
li.clear();
backInsertion(vi);
backInsertion(di);
backInsertion(li);
midInsertion(vi);
midInsertion(di);
midInsertion(li);
} ///:~Since vector does not support push_front( ), it cannot produce a front_insert_iterator. However, you can see that vector does support the other two types of insertions (even though, as you shall see later, insert( ) is not an efficient operation for vector). Note the use of the nested type Cont::value_type instead of hard-coding int.
More on stream iterators
We introduced the use of the stream iterators ostream_iterator (an output iterator) and istream_iterator (an input iterator) in conjunction with copy( ) in the previous chapter. Remember that an output stream doesn't have any concept of an “end,” since you can always just keep writing more elements. However, an input stream eventually terminates (for example, when you reach the end of a file), so you need a way to represent that. An istream_iterator has two constructors, one that takes an istream and produces the iterator you actually read from, and the other which is the default constructor and produces an object that is the past-the-end sentinel. In the following program this object is named end:
//: C07:StreamIt.cpp
// Iterators for istreams and ostreams.
#include <fstream>
#include <iostream>
#include <iterator>
#include <string>
#include <vector>
#include "../require.h"
using namespace std;
int main() {
ifstream in("StreamIt.cpp");
assure(in, "StreamIt.cpp");
istream_iterator<string> begin(in), end;
ostream_iterator<string> out(cout,
"\n");
vector<string> vs;
copy(begin, end, back_inserter(vs));
copy(vs.begin(), vs.end(), out);
*out++ = vs[0];
*out++ = "That's all, folks!";
} ///:~When in runs out of input (in this case when the end of the file is reached), init becomes equivalent to end, and the copy( ) terminates.
Because out is an ostream_iterator<string>, you can simply assign any string object to the dereferenced iterator using operator=, and that string will be placed on the output stream, as seen in the two assignments to out. Because out is defined with a newline as its second argument, these assignments also insert a newline along with each assignment.
Although it is possible to create an istream_iterator<char> and ostream_iterator<char>, these actually parse the input and thus will, for example, automatically eat whitespace (spaces, tabs, and newlines), which is not desirable if you want to manipulate an exact representation of an istream. Instead, you can use the special iterators istreambuf_iterator and ostreambuf_iterator, which are designed strictly to move characters.(104) Although these are templates, they are meant to be used with template arguments of either char or wchar_t.(105) The following example lets you compare the behavior of the stream iterators with the streambuf iterators:
//: C07:StreambufIterator.cpp
// istreambuf_iterator & ostreambuf_iterator.
#include <algorithm>
#include <fstream>
#include <iostream>
#include <iterator>
#include "../require.h"
using namespace std;
int main() {
ifstream in("StreambufIterator.cpp");
assure(in, "StreambufIterator.cpp");
// Exact representation of stream:
istreambuf_iterator<char> isb(in), end;
ostreambuf_iterator<char> osb(cout);
while(isb != end)
*osb++ = *isb++; // Copy 'in' to cout
cout << endl;
ifstream in2("StreambufIterator.cpp");
// Strips white space:
istream_iterator<char> is(in2), end2;
ostream_iterator<char> os(cout);
while(is != end2)
*os++ = *is++;
cout << endl;
} ///:~The stream iterators use the parsing defined by istream::operator>>, which is probably not what you want if you are parsing characters directly—it's fairly rare that you want all the whitespace stripped out of your character stream. You'll virtually always want to use a streambuf iterator when using characters and streams, rather than a stream iterator. In addition, istream::operator>> adds significant overhead for each operation, so it is only appropriate for higher-level operations such as parsing numbers.(106)
Manipulating raw storage
The raw_storage_iterator is defined in <memory> and is an output iterator. It is provided to enable algorithms to store their results in uninitialized memory. The interface is quite simple: the constructor takes an output iterator that is pointing to the raw memory (typically a pointer), and the operator= assigns an object into that raw memory. The template parameters are the type of the output iterator pointing to the raw storage and the type of object that will be stored. Here's an example that creates Noisy objects, which print trace statements for their construction, assignment, and destruction (we'll show the Noisy class definition later):
//: C07:RawStorageIterator.cpp {-bor}
// Demonstrate the raw_storage_iterator.
//{L} Noisy
#include <iostream>
#include <iterator>
#include <algorithm>
#include "Noisy.h"
using namespace std;
int main() {
const int QUANTITY = 10;
// Create raw storage and cast to desired type:
Noisy* np = reinterpret_cast<Noisy*>(
new char[QUANTITY * sizeof(Noisy)]);
raw_storage_iterator<Noisy*, Noisy> rsi(np);
for(int i = 0; i < QUANTITY; i++)
*rsi++ = Noisy(); // Place objects in storage
cout << endl;
copy(np, np + QUANTITY,
ostream_iterator<Noisy>(cout, "
"));
cout << endl;
// Explicit destructor call for cleanup:
for(int j = 0; j < QUANTITY; j++)
(&np[j])->~Noisy();
// Release raw storage:
delete reinterpret_cast<char*>(np);
} ///:~To make the raw_storage_iterator template happy, the raw storage must be of the same type as the objects you're creating. That's why the pointer from the new array of char is cast to a Noisy*. The assignment operator forces the objects into the raw storage using the copy-constructor. Note that the explicit destructor call must be made for proper cleanup, and this also allows the objects to be deleted one at a time during container manipulation. The expression delete np would be invalid anyway since the static type of a pointer in a delete expression must be the same as the type assigned to in the new expression.
2-5-4. The basic sequences: vector, list, deque▲
Sequences keep objects in whatever order you store them. They differ in the efficiency of their operations, however, so if you are going to manipulate a sequence in a particular fashion, choose the appropriate container for those types of manipulations. So far in this book we've been using vector as the container of choice. This is quite often the case in applications. When you start making more sophisticated uses of containers, however, it becomes important to know more about their underlying implementations and behavior so that you can make the right choices.
2-5-4-1. Basic sequence operations▲
Using a template, the following example shows the operations supported by all the basic sequences: vector, deque, and list:
//: C07:BasicSequenceOperations.cpp
// The operations available for all the
// basic sequence Containers.
#include <deque>
#include <iostream>
#include <list>
#include <vector>
using namespace std;
template<typename Container>
void print(Container& c, char* title =
"") {
cout << title << ':' << endl;
if(c.empty()) {
cout << "(empty)" << endl;
return;
}
typename Container::iterator it;
for(it = c.begin(); it != c.end(); it++)
cout << *it << " ";
cout << endl;
cout << "size() " <<
c.size()
<< " max_size() " <<
c.max_size()
<< " front() " <<
c.front()
<< " back() " <<
c.back()
<< endl;
}
template<typename ContainerOfInt> void
basicOps(char* s) {
cout << "------- " << s
<< " -------" << endl;
typedef ContainerOfInt Ci;
Ci c;
print(c, "c after default constructor");
Ci c2(10, 1); // 10 elements, values all 1
print(c2, "c2 after constructor(10,1)");
int ia[] = { 1, 3, 5, 7, 9 };
const int IASZ = sizeof(ia)/sizeof(*ia);
// Initialize with begin & end iterators:
Ci c3(ia, ia + IASZ);
print(c3, "c3 after
constructor(iter,iter)");
Ci c4(c2); // Copy-constructor
print(c4, "c4 after copy-constructor(c2)");
c = c2; // Assignment operator
print(c, "c after operator=c2");
c.assign(10, 2); // 10 elements, values all 2
print(c, "c after assign(10, 2)");
// Assign with begin & end iterators:
c.assign(ia, ia + IASZ);
print(c, "c after assign(iter, iter)");
cout << "c using reverse iterators:"
<< endl;
typename Ci::reverse_iterator rit = c.rbegin();
while(rit != c.rend())
cout << *rit++ << " ";
cout << endl;
c.resize(4);
print(c, "c after resize(4)");
c.push_back(47);
print(c, "c after push_back(47)");
c.pop_back();
print(c, "c after pop_back()");
typename Ci::iterator it = c.begin();
++it; ++it;
c.insert(it, 74);
print(c, "c after insert(it, 74)");
it = c.begin();
++it;
c.insert(it, 3, 96);
print(c, "c after insert(it, 3, 96)");
it = c.begin();
++it;
c.insert(it, c3.begin(), c3.end());
print(c, "c after insert("
"it, c3.begin(), c3.end())");
it = c.begin();
++it;
c.erase(it);
print(c, "c after erase(it)");
typename Ci::iterator it2 = it = c.begin();
++it;
++it2; ++it2; ++it2; ++it2; ++it2;
c.erase(it, it2);
print(c, "c after erase(it, it2)");
c.swap(c2);
print(c, "c after swap(c2)");
c.clear();
print(c, "c after clear()");
}
int main() {
basicOps<vector<int>
>("vector");
basicOps<deque<int> >("deque");
basicOps<list<int> >("list");
} ///:~The first function template, print( ), demonstrates the basic information you can get from any sequence container: whether it's empty, its current size, the size of the largest possible container, the element at the beginning, and the element at the end. You can also see that every container has begin( ) and end( ) member functions that return iterators.
The basicOps( ) function tests everything else (and in turn calls print( )), including a variety of constructors: default, copy-constructor, quantity and initial value, and beginning and ending iterators. There are an assignment operator= and two kinds of assign( ) member functions. One takes a quantity and an initial value, and the other takes a beginning and ending iterator.
All the basic sequence containers are reversible containers, as shown by the use of the rbegin( ) and rend( ) member functions. A sequence container can be resized, and the entire contents of the container can be removed with clear( ). When you call resize( ) to expand a sequence, the new elements use the default constructor of the type of element in the sequence, or if they are built-in types, they are zero-initialized.
Using an iterator to indicate where you want to start inserting into any sequence container, you can insert( ) a single element, a number of elements that all have the same value, and a group of elements from another container using the beginning and ending iterators of that group.
To erase( ) a single element from the middle, use an iterator; to erase( ) a range of elements, use a pair of iterators. Notice that since a list supports only bidirectional iterators, all the iterator motion must be performed with increments and decrements. (If the containers were limited to vector and deque, which produce random-access iterators, operator+ and operator- could have been used to move the iterators in bigger jumps.)
Although both list and deque support push_front( ) and pop_front( ), vector does not, but push_back( ) and pop_back( ) work with all three.
The naming of the member function swap( ) is a little confusing, since there's also a nonmember swap( ) algorithm that interchanges the values of any two objects of same type. The member swap( ) swaps everything in one container for another (if the containers hold the same type), effectively swapping the containers themselves. It does this efficiently by swapping the contents of each container, which consists mostly of pointers. The nonmember swap( ) algorithm normally uses assignment to interchange its arguments (an expensive operation for an entire container), but it is customized through template specialization to call the member swap( ) for the standard containers. There is also an iter_swap algorithm that uses iterators to interchange two elements in the same container.
The following sections discuss the particulars of each type of sequence container.
2-5-4-2. vector▲
The vector class template is intentionally made to look like a souped-up array, since it has array-style indexing, but also can expand dynamically. The vector class template is so fundamentally useful that it was introduced in a primitive way early in this book and was used regularly in previous examples. This section will give a more in-depth look at vector.
To achieve maximally-efficient indexing and iteration, vector maintains its storage as a single contiguous array of objects. This is a critical point to observe in understanding the behavior of vector. It means that indexing and iteration are lightning-fast, being basically the same as indexing and iterating over an array of objects. But it also means that inserting an object anywhere but at the end (that is, appending) is not really an acceptable operation for a vector. In addition, when a vector runs out of preallocated storage, to maintain its contiguous array it must allocate a whole new (larger) chunk of storage elsewhere and copy the objects to the new storage. This approach produces a number of unpleasant side-effects.
Cost of overflowing allocated storage
A vector starts by grabbing a block of storage, as if it's taking a guess at how many objects you plan to put in it. As long as you don't try to put in more objects than can be held in the initial block of storage, everything proceeds rapidly. (If you do know how many objects to expect, you can preallocate storage using reserve( ).) But eventually you will put in one too many objects, and the vector responds by:
- Allocating a new, bigger piece of storage.
- Copying all the objects from the old storage to the new (using the copy-constructor).
- Destroying all the old objects (the destructor is called for each one).
- Releasing the old memory.
For complex objects, this copy-construction and destruction can end up being expensive if you often overfill your vector, which is why vectors (and STL containers in general) are designed for value types (i.e. types that are cheap to copy). This includes pointers.
To see what happens when you're filling a vector, here is the Noisy class mentioned earlier. It prints information about its creations, destructions, assignments, and copy-constructions:
//: C07:Noisy.h
// A class to track various object activities.
#ifndef NOISY_H
#define NOISY_H
#include <iostream>
using std::endl;
using std::cout;
using std::ostream;
class Noisy {
static long create, assign, copycons, destroy;
long id;
public:
Noisy() : id(create++) {
cout << "d[" << id <<
"]" << endl;
}
Noisy(const Noisy& rv) : id(rv.id) {
cout << "c[" << id <<
"]" << endl;
++copycons;
}
Noisy& operator=(const Noisy& rv) {
cout << "(" << id <<
")=[" << rv.id << "]" << endl;
id = rv.id;
++assign;
return *this;
}
friend bool operator<(const Noisy& lv, const
Noisy& rv) {
return lv.id < rv.id;
}
friend bool operator==(const Noisy& lv,const
Noisy& rv) {
return lv.id == rv.id;
}
~Noisy() {
cout << "~[" << id <<
"]" << endl;
++destroy;
}
friend ostream& operator<<(ostream& os,
const Noisy& n) {
return os << n.id;
}
friend class NoisyReport;
};
struct NoisyGen {
Noisy operator()() { return Noisy(); }
};
// A Singleton. Will automatically report the
// statistics as the program terminates:
class NoisyReport {
static NoisyReport nr;
NoisyReport() {} // Private constructor
NoisyReport & operator=(NoisyReport &); //
Disallowed
NoisyReport(const NoisyReport&); //
Disallowed
public:
~NoisyReport() {
cout << "\n-------------------\n"
<< "Noisy creations: "
<< Noisy::create
<< "\nCopy-Constructions: "
<< Noisy::copycons
<< "\nAssignments: " <<
Noisy::assign
<< "\nDestructions: " <<
Noisy::destroy << endl;
}
};
#endif // NOISY_H ///:~//: C07:Noisy.cpp {O}
#include "Noisy.h"
long Noisy::create = 0, Noisy::assign = 0,
Noisy::copycons = 0, Noisy::destroy = 0;
NoisyReport NoisyReport::nr;
///:~Each Noisy object has its own identifier, and static variables keep track of all the creations, assignments (using operator=), copy-constructions, and destructions. The id is initialized using the create counter inside the default constructor; the copy-constructor and assignment operator take their id values from the rvalue. With operator= the lvalue is already an initialized object, so the old value of id is printed before it is overwritten with the id from the rvalue.
To support certain operations such as sorting and searching (which are used implicitly by some of the containers), Noisy must have an operator< and operator==. These simply compare the id values. The ostream inserter follows the usual form and simply prints the id.
Objects of type NoisyGen are function objects (since there is an operator( )) that produce Noisy objects during testing.
NoisyReport is a Singleton object(107) because we only want one report printed at program termination. It has a private constructor so no additional NoisyReport objects can be created, it disallows assignment and copy-construction, and it has a single static instance of NoisyReport called nr. The only executable statements are in the destructor, which is called as the program exits and static destructors are called. This destructor prints the statistics captured by the static variables in Noisy.
Using Noisy.h, the following program shows a vector overflowing its allocated storage:
//: C07:VectorOverflow.cpp {-bor}
// Shows the copy-construction and destruction
// that occurs when a vector must reallocate.
//{L} Noisy
#include <cstdlib>
#include <iostream>
#include <string>
#include <vector>
#include "Noisy.h"
using namespace std;
int main(int argc, char* argv[]) {
int size = 1000;
if(argc >= 2) size = atoi(argv[1]);
vector<Noisy> vn;
Noisy n;
for(int i = 0; i < size; i++)
vn.push_back(n);
cout << "\n cleaning up “ << endl;
} ///:~You can use the default value of 1000, or you can use your own value by putting it on the command line.
When you run this program, you'll see a single default constructor call (for n), then a lot of copy-constructor calls, then some destructor calls, then some more copy-constructor calls, and so on. When the vector runs out of space in the linear array of bytes it has allocated, it must (to maintain all the objects in a linear array, which is an essential part of its job) get a bigger piece of storage and move everything over, first copying and then destroying the old objects. You can imagine that if you store a lot of large and complex objects, this process could rapidly become prohibitive.
There are two solutions to this problem. The nicest one requires that you know beforehand how many objects you're going to make. In that case, you can use reserve( ) to tell the vector how much storage to preallocate, thus eliminating all the copies and destructions and making everything very fast (especially random access to the objects with operator[ ]). Note that the use of reserve( ) is different from using the vector constructor with an integral first argument; the latter initializes a prescribed number of elements using the element type's default constructor.
Generally you won't know how many objects you'll need. If vector reallocations are slowing things down, you can change sequence containers. You could use a list, butas you'll see, the deque allows speedy insertions at either end of the sequence and never needs to copy or destroy objects as it expands its storage. The deque also allows random access with operator[ ], but it's not quite as fast as vector's operator[ ]. So if you're creating all your objects in one part of the program and randomly accessing them in another, you may find yourself filling a deque and then creating a vector from the deque and using the vector for rapid indexing. You don't want to program this way habitually—just be aware of these issues (that is, avoid premature optimization).
There is a darker side to vector's reallocation of memory, however. Because vector keeps its objects in a nice, neat array, the iterators used by vector can be simple pointers. This is good—of all the sequence containers, these pointers allow the fastest selection and manipulation. Whether they are simple pointers, or whether they are iterator objects that hold an internal pointer into their container, consider what happens when you add the one additional object that causes the vector to reallocate storage and move it elsewhere. The iterator's pointer is now pointing off into nowhere:
//: C07:VectorCoreDump.cpp
// Invalidating an iterator.
#include <iterator>
#include <iostream>
#include <vector>
using namespace std;
int main() {
vector<int> vi(10, 0);
ostream_iterator<int> out(cout, " ");
vector<int>::iterator i = vi.begin();
*i = 47;
copy(vi.begin(), vi.end(), out);
cout << endl;
// Force it to move memory (could also just add
// enough objects):
vi.resize(vi.capacity() + 1);
// Now i points to wrong memory:
*i = 48; // Access violation
copy(vi.begin(), vi.end(), out); // No change to
vi[0]
} ///:~This illustrates the concept of iterator invalidation. Certain operations cause internal changes to a container's underlying data, so any iterators in effect before such changes may no longer be valid afterward. If your program is breaking mysteriously, look for places where you hold onto an iterator while adding more objects to a vector. You'll need to get a new iterator after adding elements or use operator[ ] instead for element selections. If you combine this observation with the awareness of the potential expense of adding new objects to a vector, you may conclude that the safest way to use a vector is to fill it up all at once (ideally, knowing first how many objects you'll need) and then just use it (without adding more objects) elsewhere in the program. This is the way vector has been used in the book up to this point. The Standard C++ library documents the container operations that invalidate iterators.
You may observe that using vector as the “basic” container in the earlier chapters of this book might not be the best choice in all cases. This is a fundamental issue in containers and in data structures in general—the “best” choice varies according to the way the container is used. The reason vector has been the “best” choice up until now is that it looks a lot like an array and was thus familiar and easy for you to adopt. But from now on it's also worth thinking about other issues when choosing containers.
Inserting and erasing elements
The vector is most efficient if:
- You reserve( ) the correct amount of storage at the beginning so the vector never has to reallocate.
- You only add and remove elements from the back end.
It is possible to insert and erase elements from the middle of a vector using an iterator, but the following program demonstrates what a bad idea this is:
//: C07:VectorInsertAndErase.cpp {-bor}
// Erasing an element from a vector.
//{L} Noisy
#include <algorithm>
#include <iostream>
#include <iterator>
#include <vector>
#include "Noisy.h"
using namespace std;
int main() {
vector<Noisy> v;
v.reserve(11);
cout << "11 spaces have been
reserved" << endl;
generate_n(back_inserter(v), 10, NoisyGen());
ostream_iterator<Noisy> out(cout, "
");
cout << endl;
copy(v.begin(), v.end(), out);
cout << "Inserting an element:"
<< endl;
vector<Noisy>::iterator it =
v.begin() + v.size() / 2; // Middle
v.insert(it, Noisy());
cout << endl;
copy(v.begin(), v.end(), out);
cout << "\nErasing an element:"
<< endl;
// Cannot use the previous value of it:
it = v.begin() + v.size() / 2;
v.erase(it);
cout << endl;
copy(v.begin(), v.end(), out);
cout << endl;
} ///:~When you run the program, you'll see that the call to reserve( ) really does only allocate storage—no constructors are called. The generate_n( ) call is busy: each call to NoisyGen::operator( ) results in a construction, a copy-construction (into the vector), and a destruction of the temporary. But when an object is inserted into the vector in the middle, it must shift everything down to maintain the linear array, and, since there is enough space, it does this with the assignment operator. (If the argument of reserve( ) is 10 instead of 11, it must reallocate storage.) When an object is erased from the vector, the assignment operator is once again used to move everything up to cover the place that is being erased. (Notice that this requires that the assignment operator properly clean up the lvalue.) Last, the object on the end of the array is deleted.
2-5-4-3. deque▲
The deque container is a basic sequence optimized for adding and removing elements from either end. It also allows for reasonably fast random access—it has an operator[ ] like vector. However, it does not have vector's constraint of keeping everything in a single sequential block of memory. Instead, a typical implementation of deque uses multiple blocks of sequential storage (keeping track of all the blocks and their order in a mapping structure). For this reason, the overhead for a deque to add or remove elements at either end is low. In addition, it never needs to copy and destroy contained objects during a new storage allocation (like vector does), so it is far more efficient than vector if you are adding an unknown quantity of objects at either end. This means that vector is the best choice only if you have a good idea of how many objects you need. In addition, many of the programs shown earlier in this book that use vector and push_back( ) might have been more efficient had we used a deque instead. The interface to deque differs only slightly from vector (deque has a push_front( ) and pop_front( ) while vector does not, for example), so converting code from using vector to using deque is trivial. Consider StringVector.cpp, which can be changed to use deque by replacing the word “vector” with “deque” everywhere. The following program adds parallel deque operations to the vector operations in StringVector.cpp and performs timing comparisons:
//: C07:StringDeque.cpp
// Converted from StringVector.cpp.
#include <cstddef>
#include <ctime>
#include <deque>
#include <fstream>
#include <iostream>
#include <iterator>
#include <sstream>
#include <string>
#include <vector>
#include "../require.h"
using namespace std;
int main(int argc, char* argv[]) {
char* fname = "StringDeque.cpp";
if(argc > 1) fname = argv[1];
ifstream in(fname);
assure(in, fname);
vector<string> vstrings;
deque<string> dstrings;
string line;
// Time reading into vector:
clock_t ticks = clock();
while(getline(in, line))
vstrings.push_back(line);
ticks = clock() - ticks;
cout << "Read into vector: " <<
ticks << endl;
// Repeat for deque:
ifstream in2(fname);
assure(in2, fname);
ticks = clock();
while(getline(in2, line))
dstrings.push_back(line);
ticks = clock() - ticks;
cout << "Read into deque: " <<
ticks << endl;
// Now compare indexing:
ticks = clock();
for(size_t i = 0; i < vstrings.size(); i++) {
ostringstream ss;
ss << i;
vstrings[i] = ss.str() + ":
" + vstrings[i];
}
ticks = clock() - ticks;
cout << "Indexing vector: " <<
ticks << endl;
ticks = clock();
for(size_t j = 0; j < dstrings.size(); j++) {
ostringstream ss;
ss << j;
dstrings[j] = ss.str() + ":
" + dstrings[j];
}
ticks = clock() - ticks;
cout << "Indexing deque: " <<
ticks << endl;
// Compare iteration
ofstream tmp1("tmp1.tmp"),
tmp2("tmp2.tmp");
ticks = clock();
copy(vstrings.begin(), vstrings.end(),
ostream_iterator<string>(tmp1,
"\n"));
ticks = clock() - ticks;
cout << "Iterating vector: " <<
ticks << endl;
ticks = clock();
copy(dstrings.begin(), dstrings.end(),
ostream_iterator<string>(tmp2,
"\n"));
ticks = clock() - ticks;
cout << "Iterating deque: " <<
ticks << endl;
} ///:~Knowing now what you do about the inefficiency of adding things to vector because of storage reallocation, you might expect dramatic differences between the two. However, on a 1.7 MB text file, one compiler's program produced the following (measured in platform/compiler specific clock ticks, not seconds):
Read into vector: 8350
Read into deque: 7690
Indexing vector: 2360
Indexing deque: 2480
Iterating vector: 2470
Iterating deque: 2410A different compiler and platform roughly agreed with this. It's not so dramatic, is it? This points out some important issues:
- We (programmers and authors) are typically bad at guessing where inefficiencies occur in our programs.
- Efficiency comes from a combination of effects. Here, reading the lines in and converting them to strings may dominate over the cost of vector vs. deque.
- The string class is probably fairly well designed in terms of efficiency.
This doesn't mean you shouldn't use a deque rather than a vector when you know that an uncertain number of objects will be pushed onto the end of the container. On the contrary, you should—when you're tuning for performance. But also be aware that performance issues are usually not where you think they are, and the only way to know for sure where your bottlenecks are is by testing. Later in this chapter, you'll see a more “pure” comparison of performance between vector, deque, and list.
2-5-4-4. Converting between sequences▲
Sometimes you need the behavior or efficiency of one kind of container for one part of your program, and you need a different container's behavior or efficiency in another part of the program. For example, you may need the efficiency of a deque when adding objects to the container but the efficiency of a vector when indexing them. Each of the basic sequence containers (vector, deque, and list) has a two-iterator constructor (indicating the beginning and ending of the sequence to read from when creating a new object) and an assign( ) member function to read into an existing container, so you can easily move objects from one sequence container to another.
The following example reads objects into a deque and then converts to a vector:
//: C07:DequeConversion.cpp {-bor}
// Reading into a Deque, converting to a vector.
//{L} Noisy
#include <algorithm>
#include <cstdlib>
#include <deque>
#include <iostream>
#include <iterator>
#include <vector>
#include "Noisy.h"
using namespace std;
int main(int argc, char* argv[]) {
int size = 25;
if(argc >= 2) size = atoi(argv[1]);
deque<Noisy> d;
generate_n(back_inserter(d), size, NoisyGen());
cout << "\n Converting to a
vector(1)" << endl;
vector<Noisy> v1(d.begin(), d.end());
cout << "\n Converting to a
vector(2)" << endl;
vector<Noisy> v2;
v2.reserve(d.size());
v2.assign(d.begin(), d.end());
cout << "\n Cleanup" << endl;
} ///:~You can try various sizes, but note that it makes no difference—the objects are simply copy-constructed into the new vectors. What's interesting is that v1 does not cause multiple allocations while building the vector, no matter how many elements you use. You might initially think that you must follow the process used for v2 and preallocate the storage to prevent messy reallocations, but this is unnecessary because the constructor used for v1 determines the memory requirement ahead of time.
Cost of overflowing allocated storage
It's illuminating to see what happens with a deque when it overflows a block of storage, in contrast with VectorOverflow.cpp:
//: C07:DequeOverflow.cpp {-bor}
// A deque is much more efficient than a vector when
// pushing back a lot of elements, since it doesn't
// require copying and destroying.
//{L} Noisy
#include <cstdlib>
#include <deque>
#include "Noisy.h"
using namespace std;
int main(int argc, char* argv[]) {
int size = 1000;
if(argc >= 2) size = atoi(argv[1]);
deque<Noisy> dn;
Noisy n;
for(int i = 0; i < size; i++)
dn.push_back(n);
cout << "\n cleaning up “ << endl;
} ///:~Here you will have relatively few (if any) destructors called before the words “cleaning up” appear in the output. Since the deque allocates all its storage in blocks instead of a contiguous array like vector, it never needs to move existing storage of each of its data blocks. (Thus, no additional copy-constructions and destructions occur.) The deque simply allocates a new block. For the same reason, the deque can just as efficiently add elements to the beginning of the sequence, since if it runs out of storage, it (again) just allocates a new block for the beginning. (The index block that holds the data blocks together may need to be reallocated, however.) Insertions in the middle of a deque, however, could be even messier than for vector (but not as costly).
Because of deque'sclever storage management, an existing iterator is not invalidated after you add new things to either end of a deque, as it was demonstrated to do with vector (in VectorCoreDump.cpp). If you stick to what deque is best at—insertions and removals from either end, reasonably rapid traversals and fairly fast random-access using operator[ ]—you'll be in good shape.
2-5-4-5. Checked random-access▲
Both vector and deque provide two random access functions: the indexing operator (operator[ ]), which you've seen already, and at( ), which checks the boundaries of the container that's being indexed and throws an exception if you go out of bounds. It does cost more to use at( ):
//: C07:IndexingVsAt.cpp
// Comparing "at()" to operator[].
#include <ctime>
#include <deque>
#include <iostream>
#include <vector>
#include "../require.h"
using namespace std;
int main(int argc, char* argv[]) {
long count = 1000;
int sz = 1000;
if(argc >= 2) count = atoi(argv[1]);
if(argc >= 3) sz = atoi(argv[2]);
vector<int> vi(sz);
clock_t ticks = clock();
for(int i1 = 0; i1 < count; i1++)
for(int j = 0; j < sz; j++)
vi[j];
cout << "vector[] "
<< clock() - ticks << endl;
ticks = clock();
for(int i2 = 0; i2 < count; i2++)
for(int j = 0; j < sz; j++)
vi.at(j);
cout << "vector::at() " <<
clock()-ticks <<endl;
deque<int> di(sz);
ticks = clock();
for(int i3 = 0; i3 < count; i3++)
for(int j = 0; j < sz; j++)
di[j];
cout << "deque[] " << clock() -
ticks << endl;
ticks = clock();
for(int i4 = 0; i4 < count; i4++)
for(int j = 0; j < sz; j++)
di.at(j);
cout << "deque::at() " <<
clock()-ticks <<endl;
// Demonstrate at() when you go out of bounds:
try {
di.at(vi.size() + 1);
} catch(...) {
cerr << "Exception thrown" <<
endl;
}
} ///:~As you saw in Chapter 1, different systems may handle the uncaught exception in different ways, but you'll know one way or another that something went wrong with the program when using at( ), whereas it's possible to remain ignorant when using operator[ ].
2-5-4-6. list▲
A list is implemented as a doubly linked list data structure and is thus designed for rapid insertion and removal of elements anywhere in the sequence, whereas for vector and deque this is a much more costly operation. A list is so slow when randomly accessing elements that it does not have an operator[ ]. It's best used when you're traversing a sequence, in order, from beginning to end (or vice-versa), rather than choosing elements randomly from the middle. Even then the traversal can be slower than with a vector, but if you aren't doing a lot of traversals, that won't be your bottleneck.
The memory overhead of each link in a list requires a forward and backward pointer on top of the storage for the actual object. Thus, a list is a better choice when you have larger objects that you'll be inserting and removing from the middle of the list.
It's better not to use a list if you think you might be traversing it a lot, looking for objects, since the amount of time it takes to get from the beginning of the list—which is the only place you can start unless you've already got an iterator to somewhere you know is closer to your destination—to the object of interest is proportional to the number of objects between the beginning and that object.
The objects in a list never move after they are created. “Moving” a list element means changing the links, but never copying or assigning the actual objects. This means that iterators aren't invalidated when items are added to the list as it was demonstrated earlier to be the case vector. Here's an example using a list of Noisy objects:
//: C07:ListStability.cpp {-bor}
// Things don't move around in lists.
//{L} Noisy
#include <algorithm>
#include <iostream>
#include <iterator>
#include <list>
#include "Noisy.h"
using namespace std;
int main() {
list<Noisy> l;
ostream_iterator<Noisy> out(cout, "
");
generate_n(back_inserter(l), 25, NoisyGen());
cout << "\n Printing the list:"
<< endl;
copy(l.begin(), l.end(), out);
cout << "\n Reversing the list:"
<< endl;
l.reverse();
copy(l.begin(), l.end(), out);
cout << "\n Sorting the list:"
<< endl;
l.sort();
copy(l.begin(), l.end(), out);
cout << "\n Swapping two elements:"
<< endl;
list<Noisy>::iterator it1, it2;
it1 = it2 = l.begin();
++it2;
swap(*it1, *it2);
cout << endl;
copy(l.begin(), l.end(), out);
cout << "\n Using generic reverse():
" << endl;
reverse(l.begin(), l.end());
cout << endl;
copy(l.begin(), l.end(), out);
cout << "\n Cleanup" << endl;
} ///:~Operations as seemingly radical as reversing and sorting the list require no copying of objects because, instead of moving the objects, the links are simply changed. However, notice that sort( ) and reverse( ) are member functions of list, so they have special knowledge of the internals of list and can rearrange the elements instead of copying them. On the other hand, the swap( ) function is a generic algorithm and doesn't know about list in particular, so it uses the copying approach for swapping two elements. In general, use the member version of an algorithm if that is supplied instead of its generic algorithm equivalent. In particular, use the generic sort( ) and reverse( ) algorithms only with arrays, vectors, and deques.
If you have large, complex objects, you might want to choose a list first, especially if construction, destruction, copy-construction, and assignment are expensive and if you are doing things like sorting the objects or otherwise reordering them a lot.
Special list operations
The list has some special built-in operations to make the best use of the structure of the list. You've already seen reverse( ) and sort( ). Here are some of the others:
//: C07:ListSpecialFunctions.cpp
//{L} Noisy
#include <algorithm>
#include <iostream>
#include <iterator>
#include <list>
#include "Noisy.h"
#include "PrintContainer.h"
using namespace std;
int main() {
typedef list<Noisy> LN;
LN l1, l2, l3, l4;
generate_n(back_inserter(l1), 6, NoisyGen());
generate_n(back_inserter(l2), 6, NoisyGen());
generate_n(back_inserter(l3), 6, NoisyGen());
generate_n(back_inserter(l4), 6, NoisyGen());
print(l1, "l1", " "); print(l2,
"l2", " ");
print(l3, "l3", " "); print(l4,
"l4", " ");
LN::iterator it1 = l1.begin();
++it1; ++it1; ++it1;
l1.splice(it1, l2);
print(l1, "l1 after splice(it1, l2)",
" ");
print(l2, "l2 after splice(it1, l2)",
" ");
LN::iterator it2 = l3.begin();
++it2; ++it2; ++it2;
l1.splice(it1, l3, it2);
print(l1, "l1 after splice(it1, l3, it2)",
" ");
LN::iterator it3 = l4.begin(), it4 = l4.end();
++it3; --it4;
l1.splice(it1, l4, it3, it4);
print(l1, "l1 after
splice(it1,l4,it3,it4)", " ");
Noisy n;
LN l5(3, n);
generate_n(back_inserter(l5), 4, NoisyGen());
l5.push_back(n);
print(l5, "l5 before remove()", "
");
l5.remove(l5.front());
print(l5, "l5 after remove()", "
");
l1.sort(); l5.sort();
l5.merge(l1);
print(l5, "l5 after
l5.merge(l1)", " ");
cout << "\n Cleanup" << endl;
} ///:~After filling four lists with Noisy objects, one list is spliced into another in three ways. In the first, the entire list l2 is spliced into l1 at the iterator it1. Notice that after the splice, l2 is empty—splicing means removing the elements from the source list. The second splice inserts elements from l3 starting at it2 into l1 starting at it1. The third splice starts at it1 and uses elements from l4 starting at it3 and ending at it4. The seemingly redundant mention of the source list is because the elements must be erased from the source list as part of the transfer to the destination list.
The output from the code that demonstrates remove( ) shows that the list does not have to be sorted in order for all the elements of a particular value to be removed.
Finally, if you merge( ) one list with another, the merge only works sensibly if the lists have been sorted. What you end up with in that case is a sorted list containing all the elements from both lists (the source list is erased—that is, the elements are moved to the destination list).
A unique( ) member function removes all duplicates, but only if you sort the list first:
//: C07:UniqueList.cpp
// Testing list's unique() function.
#include <iostream>
#include <iterator>
#include <list>
using namespace std;
int a[] = { 1, 3, 1, 4, 1, 5, 1, 6, 1 };
const int ASZ = sizeof a / sizeof *a;
int main() {
// For output:
ostream_iterator<int> out(cout, " ");
list<int> li(a, a + ASZ);
li.unique();
// Oops! No duplicates removed:
copy(li.begin(), li.end(), out);
cout << endl;
// Must sort it first:
li.sort();
copy(li.begin(), li.end(), out);
cout << endl;
// Now unique() will have an effect:
li.unique();
copy(li.begin(), li.end(), out);
cout << endl;
} ///:~The list constructor used here takes the starting and past-the-end iterator from another container and copies all the elements from that container into itself. Here, the “container” is just an array, and the “iterators” are pointers into that array, but because of the design of the STL, the list constructor works with arrays just as easily as with any other container.
The unique( ) function will remove only adjacent duplicate elements, and thus sorting is typically necessary before calling unique( ). The exception is when the problem you're trying to solve includes eliminating adjacent duplicates according to the current ordering.
Four additional list member functions are not demonstrated here: a remove_if( ) that takes a predicate, which decides whether an object should be removed; a unique( ) that takes a binary predicate to perform uniqueness comparisons; a merge( ) that takes an additional argument which performs comparisons; and a sort( ) that takes a comparator (to provide a comparison or override the existing one).
list vs. set
Looking at the previous example, you might note that if you want a sorted sequence with no duplicates, you could get that result with a set. It's interesting to compare the performance of the two containers:
//: C07:ListVsSet.cpp
// Comparing list and set performance.
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <iterator>
#include <list>
#include <set>
#include "PrintContainer.h"
using namespace std;
class Obj {
int a[20]; // To take up extra space
int val;
public:
Obj() : val(rand() % 500) {}
friend bool
operator<(const Obj& a, const Obj& b) {
return a.val < b.val;
}
friend bool
operator==(const Obj& a, const Obj& b) {
return a.val == b.val;
}
friend ostream&
operator<<(ostream& os, const Obj& a) {
return os << a.val;
}
};
struct ObjGen {
Obj operator()() { return Obj(); }
};
int main() {
const int SZ = 5000;
srand(time(0));
list<Obj> lo;
clock_t ticks = clock();
generate_n(back_inserter(lo), SZ, ObjGen());
lo.sort();
lo.unique();
cout << "list:" << clock() -
ticks << endl;
set<Obj> so;
ticks = clock();
generate_n(inserter(so, so.begin()),
SZ, ObjGen());
cout << "set:" << clock() -
ticks << endl;
print(lo);
print(so);
} ///:~When you run the program, you should discover that set is much faster than list. This is reassuring—after all, it is set's primary job description to hold only unique elements in sorted order!
This example uses the header PrintContainer.h, which contains a function template that prints any sequence container to an output stream. PrintContainer.h is defined as follows:
//:
C07:PrintContainer.h
// Prints a
sequence container
#ifndef
PRINT_CONTAINER_H
#define
PRINT_CONTAINER_H
#include
"../C06/PrintSequence.h"
template<class
Cont>
void
print(Cont& c, const char* nm = "",
const char* sep = "\n",
std::ostream&
os = std::cout) {
print(c.begin(), c.end(), nm, sep, os);
}
#endif ///:~The print( ) template defined here just calls the print( ) function template we defined in the previous chapter in PrintSequence.h.
2-5-4-7. Swapping sequences▲
We mentioned earlier that all basic sequences have a member function swap( ) that's designed to switch one sequence with another (but only for sequences of the same type). The member swap( ) makes use of its knowledge of the internal structure of the particular container in order to be efficient:
//: C07:Swapping.cpp {-bor}
// All basic sequence containers can be swapped.
//{L} Noisy
#include <algorithm>
#include <deque>
#include <iostream>
#include <iterator>
#include <list>
#include <vector>
#include "Noisy.h"
#include "PrintContainer.h"
using namespace std;
ostream_iterator<Noisy> out(cout, " ");
template<class Cont> void testSwap(char* cname) {
Cont c1, c2;
generate_n(back_inserter(c1), 10, NoisyGen());
generate_n(back_inserter(c2), 5, NoisyGen());
cout << endl << cname <<
":" << endl;
print(c1, "c1"); print(c2, "c2");
cout << "\n Swapping the " <<
cname << ":" << endl;
c1.swap(c2);
print(c1, "c1"); print(c2, "c2");
}
int main() {
testSwap<vector<Noisy> >("vector");
testSwap<deque<Noisy>
>("deque");
testSwap<list<Noisy> >("list");
} ///:~When you run this, you'll discover that each type of sequence container can swap one sequence for another without any copying or assignments, even if the sequences are of different sizes. In effect, you're completely swapping the resources of one object for another.
The STL algorithms also contain a swap( ), and when this function is applied to two containers of the same type, it uses the member swap( ) to achieve fast performance. Consequently, if you apply the sort( ) algorithm to a container of containers, you will find that the performance is very fast—it turns out that fast sorting of a container of containers was a design goal of the STL.
2-5-5. set▲
The set container accepts only one copy of each element. It also sorts the elements. (Sorting isn't intrinsic to the conceptual definition of a set, but the STL set stores its elements in a balanced tree data structure to provide rapid lookups, thus producing sorted results when you traverse it.) The first two examples in this chapter used sets.
Consider the problem of creating an index for a book. You might like to start with all the words in the book, but you only want one instance of each word, and you want them sorted. A set is perfect for this and solves the problem effortlessly. However, there's also the problem of punctuation and any other nonalpha characters, which must be stripped off to generate proper words. One solution to this problem is to use the Standard C library functions isalpha( ) and isspace( ) to extract only the characters you want. You can replace all unwanted characters with spaces so that you can easily extract valid words from each line you read:
//: C07:WordList.cpp
// Display a list of words used in a document.
#include <algorithm>
#include <cctype>
#include <cstring>
#include <fstream>
#include <iostream>
#include <iterator>
#include <set>
#include <sstream>
#include <string>
#include "../require.h"
using namespace std;
char replaceJunk(char c) {
// Only keep alphas, space (as a delimiter), and '
return (isalpha(c) || c == '\'') ? c : ' ';
}
int main(int argc, char* argv[]) {
char* fname = "WordList.cpp";
if(argc > 1) fname = argv[1];
ifstream in(fname);
assure(in, fname);
set<string> wordlist;
string line;
while(getline(in, line)) {
transform(line.begin(), line.end(), line.begin(),
replaceJunk);
istringstream is(line);
string word;
while(is >> word)
wordlist.insert(word);
}
// Output results:
copy(wordlist.begin(), wordlist.end(),
ostream_iterator<string>(cout,
"\n"));
} ///:~The call to transform( ) replaces each character to be ignored with a space. The set container not only ignores duplicate words, but compares the words it keeps according to the function object less<string> (the default second template argument for the set container), which in turn uses string::operator<( ), so the words emerge in alphabetical order.
You don't need to use a set just to get a sorted sequence. You can use the sort( ) function (along with a multitude of other functions in the STL) on different STL containers. However, it's likely that set will be faster here. Using a set is particularly handy when you just want to do lookup, since its find( ) member function has logarithmic complexity and so is much faster than the generic find( ) algorithm. As you recall, the generic find( ) algorithm needs to traverse the whole range until it finds the search element (resulting in a worst-case complexity of N, and an average complexity of N/2). However, if you have a sequence container that is already sorted, use equal_range( ) for logarithmic complexity when finding elements.
The following version shows how to build the list of words with an istreambuf_iterator that moves the characters from one place (the input stream) to another (a string object), depending on whether the Standard C library function isalpha( ) returns true:
//: C07:WordList2.cpp
// Illustrates istreambuf_iterator and insert
iterators.
#include <cstring>
#include <fstream>
#include <iostream>
#include <iterator>
#include <set>
#include <string>
#include "../require.h"
using namespace std;
int main(int argc, char* argv[]) {
char* fname = "WordList2.cpp";
if(argc > 1) fname = argv[1];
ifstream in(fname);
assure(in, fname);
istreambuf_iterator<char> p(in), end;
set<string> wordlist;
while(p != end) {
string word;
insert_iterator<string> ii(word, word.begin());
// Find the first alpha character:
while(p != end && !isalpha(*p))
++p;
// Copy until the first non-alpha character:
while(p != end && isalpha(*p))
*ii++ = *p++;
if(word.size() != 0)
wordlist.insert(word);
}
// Output results:
copy(wordlist.begin(), wordlist.end(),
ostream_iterator<string>(cout,
"\n"));
} ///:~This example was suggested by Nathan Myers, who invented the istreambuf_iterator and its relatives. This iterator extracts information character by character from a stream. Although the istreambuf_iterator template argument might imply that you could extract, for example, ints instead of char, that's not the case. The argument must be of some character type—a regular char or a wide character.
After the file is open, an istreambuf_iterator called p is attached to the istream so characters can be extracted from it. The set<string> called wordlist will hold the resulting words.
The while loop reads words until it finds the end of the input stream. This is detected using the default constructor for istreambuf_iterator, which produces the past-the-end iterator object end. Thus, if you want to test to make sure you're not at the end of the stream, you simply say p != end.
The second type of iterator that's used here is the insert_iterator, which you saw previously. This inserts objects into a container. Here, the “container” is the string called word, which, for the purposes of insert_iterator, behaves like a container. The constructor for insert_iterator requires the container and an iterator indicating where it should start inserting the characters. You could also use a back_insert_iterator, which requires that the container have a push_back( ) (string does).
After the while loop sets everything up, it begins by looking for the first alpha character, incrementing start until that character is found. It then copies characters from one iterator to the other, stopping when a nonalpha character is found. Each word, assuming it is nonempty, is added to wordlist.
2-5-5-1. A completely reusable tokenizer▲
The word list examples use different approaches to extract tokens from a stream, neither of which is very flexible. Since the STL containers and algorithms all revolve around iterators, the most flexible solution will itself use an iterator. You could think of the TokenIterator as an iterator that wraps itself around any other iterator that can produce characters. Because it is certainly a type of input iterator (the most primitive type of iterator), it can provide input to any STL algorithm. Not only is it a useful tool in itself, the following TokenIterator is also a good example of how you can design your own iterators.(108)
The TokenIterator class is doubly flexible. First, you can choose the type of iterator that will produce the char input. Second, instead of just saying what characters represent the delimiters, TokenIterator will use a predicate that is a function object whose operator( ) takes a char and decides whether it should be in the token. Although the two examples given here have a static concept of what characters belong in a token, you could easily design your own function object to change its state as the characters are read, producing a more sophisticated parser.
The following header file contains two basic predicates, Isalpha and Delimiters, along with the template for TokenIterator:
//: C07:TokenIterator.h
#ifndef TOKENITERATOR_H
#define TOKENITERATOR_H
#include <algorithm>
#include <cctype>
#include <functional>
#include <iterator>
#include <string>
struct Isalpha : std::unary_function<char, bool>
{
bool operator()(char c) { return std::isalpha(c); }
};
class Delimiters : std::unary_function<char,
bool> {
std::string exclude;
public:
Delimiters() {}
Delimiters(const std::string& excl) :
exclude(excl) {}
bool operator()(char c) {
return exclude.find(c) == std::string::npos;
}
};
template<class InputIter, class Pred = Isalpha>
class TokenIterator : public std::iterator<
std::input_iterator_tag, std::string,
std::ptrdiff_t> {
InputIter first;
InputIter last;
std::string word;
Pred predicate;
public:
TokenIterator(InputIter begin, InputIter end,
Pred pred = Pred())
: first(begin), last(end), predicate(pred) {
++*this;
}
TokenIterator() {} // End sentinel
// Prefix increment:
TokenIterator& operator++() {
word.resize(0);
first = std::find_if(first, last, predicate);
while(first != last && predicate(*first))
word += *first++;
return *this;
}
// Postfix increment
class CaptureState {
std::string word;
public:
CaptureState(const std::string& w) : word(w) {}
std::string operator*() { return word; }
};
CaptureState operator++(int) {
CaptureState d(word);
++*this;
return d;
}
// Produce the actual value:
std::string operator*() const { return word; }
const std::string* operator->() const { return
&word; }
// Compare iterators:
bool operator==(const TokenIterator&) {
return word.size() == 0 && first == last;
}
bool operator!=(const TokenIterator& rv) {
return !(*this == rv);
}
};
#endif // TOKENITERATOR_H ///:~The TokenIterator class derives from the std::iterator template. It might appear that some kind of functionality comes with std::iterator, but it is purely a way of tagging an iterator, to tell a container that uses it what it can do. Here, you can see input_iterator_tag as the iterator_category template argument—this tells anyone who asks that a TokenIterator only has the capabilities of an input iterator and cannot be used with algorithms requiring more sophisticated iterators. Apart from the tagging, std::iterator doesn't do anything beyond providing several useful type definitions. You must implement all other functionality yourself.
The TokenIterator class may look a little strange at first, because the first constructor requires both a “begin” and an “end” iterator as arguments, along with the predicate. Remember, this is a “wrapper” iterator that has no idea how to tell when it's at the end of its input, so the ending iterator is necessary in the first constructor. The reason for the second (default) constructor is that the STL algorithms (and any algorithms you write) need a TokenIterator sentinel to be the past-the-end value. Since all the information necessary to see if the TokenIterator has reached the end of its input is collected in the first constructor, this second constructor creates a TokenIterator that is merely used as a placeholder in algorithms.
The core of the behavior happens in operator++. This erases the current value of word using string::resize( ) and then finds the first character that satisfies the predicate (thus discovering the beginning of the new token) using find_if( ). The resulting iterator is assigned to first, thus moving first forward to the beginning of the token. Then, as long as the end of the input is not reached and the predicate is satisfied, input characters are copied into word. Finally, the TokenIterator object is returned and must be dereferenced to access the new token.
The postfix increment requires an object of type CaptureState to hold the value before the increment, so it can be returned. Producing the actual value is a straightforward operator*. The only other functions to define for an output iterator are the operator== and operator!= to indicate whether the TokenIterator has reached the end of its input. You can see that the argument for operator== is ignored—it only cares about whether it has reached its internal last iterator. Notice that operator!= is defined in terms of operator==.
A good test of TokenIterator includes a number of different sources of input characters, including a streambuf_iterator, a char*, and a deque<char>::iterator. Finally, the original word list problem is solved:
//: C07:TokenIteratorTest.cpp {-g++}
#include <fstream>
#include <iostream>
#include <vector>
#include <deque>
#include <set>
#include "TokenIterator.h"
#include "../require.h"
using namespace std;
int main(int argc, char* argv[]) {
char* fname = "TokenIteratorTest.cpp";
if(argc > 1) fname = argv[1];
ifstream in(fname);
assure(in, fname);
ostream_iterator<string> out(cout,
"\n");
typedef istreambuf_iterator<char> IsbIt;
IsbIt begin(in), isbEnd;
Delimiters delimiters("
\t\n~;()\"<>:{}[]+-=&*#.,/\\");
TokenIterator<IsbIt, Delimiters>
wordIter(begin, isbEnd, delimiters), end;
vector<string> wordlist;
copy(wordIter, end, back_inserter(wordlist));
// Output results:
copy(wordlist.begin(), wordlist.end(), out);
*out++ =
"-----------------------------------";
// Use a char array as the source:
char* cp = "typedef
std::istreambuf_iterator<char> It";
TokenIterator<char*, Delimiters>
charIter(cp, cp + strlen(cp), delimiters), end2;
vector<string> wordlist2;
copy(charIter, end2, back_inserter(wordlist2));
copy(wordlist2.begin(), wordlist2.end(), out);
*out++ =
"-----------------------------------";
// Use a deque<char> as the source:
ifstream in2("TokenIteratorTest.cpp");
deque<char> dc;
copy(IsbIt(in2), IsbIt(), back_inserter(dc));
TokenIterator<deque<char>::iterator,Delimiters>
dcIter(dc.begin(), dc.end(), delimiters), end3;
vector<string> wordlist3;
copy(dcIter, end3, back_inserter(wordlist3));
copy(wordlist3.begin(), wordlist3.end(), out);
*out++ =
"-----------------------------------";
// Reproduce the Wordlist.cpp example:
ifstream in3("TokenIteratorTest.cpp");
TokenIterator<IsbIt, Delimiters>
wordIter2(IsbIt(in3), isbEnd, delimiters);
set<string> wordlist4;
while(wordIter2 != end)
wordlist4.insert(*wordIter2++);
copy(wordlist4.begin(), wordlist4.end(), out);
} ///:~When using an istreambuf_iterator, you create one to attach to the istream object and one with the default constructor as the past-the-end marker. Both are used to create the TokenIterator that will produce the tokens; the default constructor produces the faux TokenIterator past-the-end sentinel. (This is just a placeholder and is ignored.) The TokenIterator produces strings that are inserted into a container of string—here a vector<string> is used in all cases except the last. (You could also concatenate the results onto a string.) Other than that, a TokenIterator works like any other input iterator.
When defining a bidirectional (and therefore also a random access) iterator, you can get reverse iterators “for free” by using the std::reverse_iterator adaptor. If you have already defined an iterator for a container with bidirectional capabilities, you can get a reverse iterator from your forward-traversing iterator with lines like the following inside your container class:
// Assume "iterator" is your nested iterator type
typedef std::reverse_iterator<iterator>
reverse_iterator;
reverse_iterator rbegin() {return
reverse_iterator(end());
reverse_iterator rend() {return
reverse_iterator(begin());The std::reverse_iterator adaptor does all the work for you. For example, if you use the * operator to dereference your reverse iterator, it automatically decrements a temporary copy of the forward iterator it is holding in order to return the correct element, since reverse iterators logically point one position past the element they refer to.
2-5-6. stack▲
The stack container, along with queue and priority_queue, are classified as adaptors, which means they adapt one of the basic sequence containers to store their data. This is an unfortunate case of confusing what something does with the details of its underlying implementation—the fact that these are called “adaptors” is of primary value only to the creator of the library. When you use them, you generally don't care that they're adaptors, but instead that they solve your problem. Admittedly it's useful at times to know that you can choose an alternate implementation or build an adaptor from an existing container object, but that's generally one level removed from the adaptor's behavior. So, while you may see it emphasized elsewhere that a particular container is an adaptor, we'll only point out that fact when it's useful. Note that each type of adaptor has a default container that it's built upon, and this default is the most sensible implementation. In most cases you won't need to concern yourself with the underlying implementation.
The following example shows stack<string> implemented in the three ways: the default (which uses deque), then with a vector, and finally with a list:
//: C07:Stack1.cpp
// Demonstrates the STL stack.
#include <fstream>
#include <iostream>
#include <list>
#include <stack>
#include <string>
#include <vector>
using namespace std;
// Rearrange comments below to use different versions.
typedef stack<string> Stack1; // Default:
deque<string>
// typedef stack<string, vector<string> >
Stack2;
// typedef stack<string, list<string> >
Stack3;
int main() {
ifstream in("Stack1.cpp");
Stack1 textlines; // Try the different versions
// Read file and store lines in the stack:
string line;
while(getline(in, line))
textlines.push(line + "\n");
// Print lines from the stack and pop them:
while(!textlines.empty()) {
cout << textlines.top();
textlines.pop();
}
} ///:~The top( ) and pop( ) operations will probably seem non-intuitive if you've used other stack classes. When you call pop( ), it returns void rather than the top element that you might have expected. If you want the top element, you get a reference to it with top( ). It turns out this is more efficient, since a traditional pop( ) must return a value rather than a reference and thus invokes the copy-constructor. More important, it is exception safe, as we discussed in Chapter 1. If pop( ) both changed the state of the stack and attempted to return the top element, an exception in the element's copy-constructor could cause the element to be lost. When you're using a stack (or a priority_queue, described later), you can efficiently refer to top( ) as many times as you want and then discard the top element explicitly using pop( ). (Perhaps if some term other than the familiar “pop” had been used, this would have been a bit clearer.)
The stack template has a simple interface—essentially the member functions you saw earlier. Since it only makes sense to access a stack at its top, no iterators are available for traversing it. Nor are there sophisticated forms of initialization, but if you need that, you can use the underlying container upon which the stack is implemented. For example, suppose you have a function that expects a stack interface, but in the rest of your program you need the objects stored in a list. The following program stores each line of a file along with the leading number of spaces in that line. (You might imagine it as a starting point for performing some kind of source-code reformatting.)
//: C07:Stack2.cpp
// Converting a list to a stack.
#include <iostream>
#include <fstream>
#include <stack>
#include <list>
#include <string>
#include <cstddef>
using namespace std;
// Expects a stack:
template<class Stk>
void stackOut(Stk& s, ostream& os = cout) {
while(!s.empty()) {
os << s.top() << "\n";
s.pop();
}
}
class Line {
string line; // Without leading spaces
size_t lspaces; // Number of leading spaces
public:
Line(string s) : line(s) {
lspaces = line.find_first_not_of(' ');
if(lspaces == string::npos)
lspaces = 0;
line = line.substr(lspaces);
}
friend ostream& operator<<(ostream& os,
const Line& l) {
for(size_t i = 0; i < l.lspaces; i++)
os << ' ';
return os << l.line;
}
// Other functions here...
};
int main() {
ifstream in("Stack2.cpp");
list<Line> lines;
// Read file and store lines in the list:
string s;
while(getline(in, s))
lines.push_front(s);
// Turn the list into a stack for printing:
stack<Line, list<Line> > stk(lines);
stackOut(stk);
} ///:~The function that requires the stack interface just sends each top( ) object to an ostream and then removes it by calling pop( ). The Line class determines the number of leading spaces and then stores the contents of the line without the leading spaces. The ostream operator<< re-inserts the leading spaces so the line prints properly, but you can easily change the number of spaces by changing the value of lspaces. (The member functions to do this are not shown here.) In main( ), the input file is read into a list<Line>, and then each line in the list is copied into a stack that is sent to stackOut( ).
You cannot iterate through a stack; this emphasizes that you only want to perform stack operations when you create a stack. You can get equivalent “stack” functionality using a vector and its back( ), push_back( ), and pop_back( ) member functions, and then you have all the additional functionality of the vector. The program Stack1.cpp can be rewritten to show this:
//: C07:Stack3.cpp
// Using a vector as a stack; modified Stack1.cpp.
#include <fstream>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int main() {
ifstream in("Stack3.cpp");
vector<string> textlines;
string line;
while(getline(in, line))
textlines.push_back(line + "\n");
while(!textlines.empty()) {
cout << textlines.back();
textlines.pop_back();
}
} ///:~This produces the same output as Stack1.cpp, but you can now perform vector operations as well. A list can also push things at the front, but it's generally less efficient than using push_back( ) with vector. (In addition, deque is usually more efficient than list for pushing things at the front.)
2-5-7. queue▲
The queue container is a restricted form of a deque—you can only enter elements at one end and pull them off the other end. Functionally, you could use a deque anywhere you need a queue, and you would then also have the additional functionality of the deque. The only reason you need to use a queue rather than a deque, then, is when you want to emphasize that you will only be performing queue-like behavior.
The queue class is an adaptor like stack, in that it is built on top of another sequence container. As you might guess, the ideal implementation for a queue is a deque, and that is the default template argument for the queue; you'll rarely need a different implementation.
Queues are often used if you want to model a system where some elements are waiting to be served by other elements in the system. A classic example of this is the “bank-teller problem.” Customers arrive at random intervals, get into a line, and then are served by a set of tellers. Since the customers arrive randomly and each takes a random amount of time to be served, there's no way to deterministically know how long the line will be at any time. However, it's possible to simulate the situation and see what happens.
In a realistic simulation each customer and teller should be run by a separate thread. What we'd like is a multithreaded environment so that each customer or teller would have his own thread. However, Standard C++ has no support for multithreading. On the other hand, with a little adjustment to the code, it's possible to simulate enough multithreading to provide a satisfactory solution.(109)
In multithreading, multiple threads of control run simultaneously, sharing the same address space. Quite often you have fewer CPUs than you do threads (and often only one CPU). To give the illusion that each thread has its own CPU, a time-slicing mechanism says “OK, current thread, you've had enough time. I'm going to stop you and give time to some other thread.” This automatic stopping and starting of threads is called preemptive, and it means you (the programmer) don't need to manage the threading process.
An alternative approach has each thread voluntarily yield the CPU to the scheduler, which then finds another thread that needs running. Instead, we'll build the “time-slicing” into the classes in the system. Here, it will be the tellers that represent the “threads,” (the customers will be passive). Each teller will have an infinite-looping run( ) member function that will execute for a certain number of “time units” and then simply return. By using the ordinary return mechanism, we eliminate the need for any swapping. The resulting program, although small, provides a remarkably reasonable simulation:
//: C07:BankTeller.cpp {RunByHand}
// Using a queue and simulated multithreading
// to model a bank teller system.
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <iterator>
#include <list>
#include <queue>
using namespace std;
class Customer {
int serviceTime;
public:
Customer() : serviceTime(0) {}
Customer(int tm) : serviceTime(tm) {}
int getTime() { return serviceTime; }
void setTime(int newtime) { serviceTime = newtime; }
friend ostream&
operator<<(ostream& os, const Customer&
c) {
return os << '[' << c.serviceTime
<< ']';
}
};
class Teller {
queue<Customer>& customers;
Customer current;
enum { SLICE = 5 };
int ttime; // Time left in slice
bool busy; // Is teller serving a customer?
public:
Teller(queue<Customer>& cq)
: customers(cq), ttime(0), busy(false) {}
Teller& operator=(const Teller& rv) {
customers = rv.customers;
current = rv.current;
ttime = rv.ttime;
busy = rv.busy;
return *this;
}
bool isBusy() { return busy; }
void run(bool recursion = false) {
if(!recursion)
ttime = SLICE;
int servtime = current.getTime();
if(servtime > ttime) {
servtime -= ttime;
current.setTime(servtime);
busy = true; // Still working on current
return;
}
if(servtime < ttime) {
ttime -= servtime;
if(!customers.empty()) {
current = customers.front();
customers.pop(); // Remove it
busy = true;
run(true); // Recurse
}
return;
}
if(servtime == ttime) {
// Done with current, set to empty:
current = Customer(0);
busy = false;
return; // No more time in this slice
}
}
};
// Inherit to access protected implementation:
class CustomerQ : public queue<Customer> {
public:
friend ostream&
operator<<(ostream& os, const
CustomerQ& cd) {
copy(cd.c.begin(), cd.c.end(),
ostream_iterator<Customer>(os,
""));
return os;
}
};
int main() {
CustomerQ customers;
list<Teller> tellers;
typedef list<Teller>::iterator TellIt;
tellers.push_back(Teller(customers));
srand(time(0)); // Seed the random number generator
clock_t ticks = clock();
// Run simulation for at least 5 seconds:
while(clock() < ticks + 5 * CLOCKS_PER_SEC) {
// Add a random number of customers to the
// queue, with random service times:
for(int i = 0; i < rand() % 5; i++)
customers.push(Customer(rand() % 15 + 1));
cout << '{' << tellers.size() <<
'}'
<< customers << endl;
// Have the tellers service the queue:
for(TellIt i = tellers.begin();
i != tellers.end(); i++)
(*i).run();
cout << '{' << tellers.size() <<
'}'
<< customers << endl;
// If line is too long, add another teller:
if(customers.size() / tellers.size() > 2)
tellers.push_back(Teller(customers));
// If line is short enough, remove a teller:
if(tellers.size() > 1 &&
customers.size() / tellers.size() < 2)
for(TellIt i = tellers.begin();
i != tellers.end(); i++)
if(!(*i).isBusy()) {
tellers.erase(i);
break; // Out of for loop
}
}
} ///:~Each customer requires a certain amount of service time, which is the number of time units that a teller must spend on the customer to serve that customer's needs. The amount of service time will be different for each customer and will be determined randomly. In addition, you won't know how many customers will be arriving in each interval, so this will also be determined randomly.
The Customer objects are kept in a queue<Customer>, and each Teller object keeps a reference to that queue.When a Teller object is finished with its current Customer object, that Teller will get another Customer from the queue and begin working on the new Customer, reducing the Customer's service time during each time slice that the Teller is allotted. All this logic is in the run( ) member function, which is basically a three-way if statement based on whether the amount of time necessary to serve the customer is less than, greater than, or equal to the amount of time left in the teller's current time slice. Notice that if the Teller has more time after finishing with a Customer, it gets a new customer and recurses into itself.
Just as with a stack, when you use a queue, it's only a queue and doesn't have any of the other functionality of the basic sequence containers. This includes the ability to get an iterator in order to step through the stack. However, the underlying sequence container (that the queue is built upon) is held as a protected member inside the queue, and the identifier for this member is specified in the C++ Standard as ‘c', which means that you can derive from queue to access the underlying implementation. The CustomerQ class does exactly that, for the sole purpose of defining an ostream operator<< that can iterate through the queue and display its members.
The driver for the simulation is the while loop in main( ), which uses processor ticks (defined in <ctime>) to determine if the simulation has run for at least 5 seconds. At the beginning of each pass through the loop, a random number of customers is added, with random service times. Both the number of tellers and the queue contents are displayed so you can see the state of the system. After running each teller, the display is repeated. At this point, the system adapts by comparing the number of customers and the number of tellers. If the line is too long, another teller is added, and if it is short enough, a teller can be removed. In this adaptation section of the program you can experiment with policies regarding the optimal addition and removal of tellers. If this is the only section that you're modifying, you might want to encapsulate policies inside different objects.
We'll revisit this example in a multithreaded exercise in Chapter 11.
2-5-8. Priority queues▲
When you push( ) an object onto a priority_queue, that object is sorted into the queue according to a comparison function or function object. (You can allow the default less template to supply this, or you can provide one of your own.) The priority_queue ensures that when you look at the top( ) element, it will be the one with the highest priority. When you're done with it, you call pop( ) to remove it and bring the next one into place. Thus, the priority_queue has nearly the same interface as a stack, but it behaves differently.
Like stack and queue, priority_queue is an adaptor that is built on top of one of the basic sequences—the default sequence being vector.
It's trivial to make a priority_queue that works with ints:
//: C07:PriorityQueue1.cpp
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <queue>
using namespace std;
int main() {
priority_queue<int> pqi;
srand(time(0)); // Seed the random number generator
for(int i = 0; i < 100; i++)
pqi.push(rand() % 25);
while(!pqi.empty()) {
cout << pqi.top() << ' ';
pqi.pop();
}
} ///:~This pushes into the priority_queue 100 random values from 0 to 24. When you run this program you'll see that duplicates are allowed, and the highest values appear first. To show how you can change the ordering by providing your own function or function object, the following program gives lower-valued numbers the highest priority:
//: C07:PriorityQueue2.cpp
// Changing the priority.
#include <cstdlib>
#include <ctime>
#include <functional>
#include <iostream>
#include <queue>
using namespace std;
int main() {
priority_queue<int, vector<int>,
greater<int> > pqi;
srand(time(0));
for(int i = 0; i < 100; i++)
pqi.push(rand() % 25);
while(!pqi.empty()) {
cout << pqi.top() << ' ';
pqi.pop();
}
} ///:~A more interesting problem is a to-do list, where each object contains a string and a primary and secondary priority value:
//: C07:PriorityQueue3.cpp
// A more complex use of priority_queue.
#include <iostream>
#include <queue>
#include <string>
using namespace std;
class ToDoItem {
char primary;
int secondary;
string item;
public:
ToDoItem(string td, char pri = 'A', int sec = 1)
: primary(pri), secondary(sec), item(td) {}
friend bool operator<(
const ToDoItem& x, const ToDoItem& y) {
if(x.primary > y.primary)
return true;
if(x.primary == y.primary)
if(x.secondary > y.secondary)
return true;
return false;
}
friend ostream&
operator<<(ostream& os, const ToDoItem&
td) {
return os << td.primary << td.secondary
<< ": " << td.item;
}
};
int main() {
priority_queue<ToDoItem> toDoList;
toDoList.push(ToDoItem("Empty trash", 'C',
4));
toDoList.push(ToDoItem("Feed dog", 'A',
2));
toDoList.push(ToDoItem("Feed bird", 'B',
7));
toDoList.push(ToDoItem("Mow lawn", 'C',
3));
toDoList.push(ToDoItem("Water lawn", 'A',
1));
toDoList.push(ToDoItem("Feed cat", 'B',
1));
while(!toDoList.empty()) {
cout << toDoList.top() << endl;
toDoList.pop();
}
} ///:~The ToDoItem's operator< must be a nonmember function for it to work with less< >. Other than that, everything happens automatically. The output is
A1: Water lawn
A2: Feed dog
B1: Feed cat
B7: Feed bird
C3: Mow lawn
C4: Empty trashYou cannot iterate through a priority_queue, but it's possible to simulate the behavior of a priority_queue using a vector, thus allowing you access to that vector. You can do this by looking at the implementation of priority_queue, which uses make_heap( ), push_heap( ), and pop_heap( ). (These are the soul of the priority_queue—in fact you could say that the heap is the priority queue and that priority_queueis just a wrapper around it.) This turns out to be reasonably straightforward, but you might think that a shortcut is possible. Since the container used by priority_queue is protected (and has the identifier, according to the Standard C++ specification, named c), you can inherit a new class that provides access to the underlying implementation:
//: C07:PriorityQueue4.cpp
// Manipulating the underlying implementation.
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <iterator>
#include <queue>
using namespace std;
class PQI : public priority_queue<int> {
public:
vector<int>& impl() { return c; }
};
int main() {
PQI pqi;
srand(time(0));
for(int i = 0; i < 100; i++)
pqi.push(rand() % 25);
copy(pqi.impl().begin(), pqi.impl().end(),
ostream_iterator<int>(cout, " "));
cout << endl;
while(!pqi.empty()) {
cout << pqi.top() << ' ';
pqi.pop();
}
} ///:~However, if you run this program, you'll discover that the vector doesn't contain the items in the descending order that you get when you call pop( ), the order that you want from the priority queue. It would seem that if you want to create a vector that is a priority queue, you have to do it by hand, like this:
//: C07:PriorityQueue5.cpp
// Building your own priority queue.
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <iterator>
#include <queue>
using namespace std;
template<class T, class Compare>
class PQV : public vector<T> {
Compare comp;
public:
PQV(Compare cmp = Compare()) : comp(cmp) {
make_heap(this->begin(),this->end(), comp);
}
const T& top() { return this->front(); }
void push(const T& x) {
this->push_back(x);
push_heap(this->begin(),this->end(), comp);
}
void pop() {
pop_heap(this->begin(),this->end(), comp);
this->pop_back();
}
};
int main() {
PQV< int, less<int> > pqi;
srand(time(0));
for(int i = 0; i < 100; i++)
pqi.push(rand() % 25);
copy(pqi.begin(), pqi.end(),
ostream_iterator<int>(cout, " "));
cout << endl;
while(!pqi.empty()) {
cout << pqi.top() << ' ';
pqi.pop();
}
} ///:~But this program behaves in the same way as the previous one! What you are seeing in the underlying vector is called a heap.This heap data structure represents the tree of the priority queue (stored in the linear structure of the vector), but when you iterate through it, you do not get a linear priority-queue order. You might think that you can simply call sort_heap( ), but that only works once, and then you don't have a heap anymore, but instead a sorted list. This means that to go back to using it as a heap, the user must remember to call make_heap( ) first. This can be encapsulated into your custom priority queue:
//: C07:PriorityQueue6.cpp
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <iterator>
#include <queue>
using namespace std;
template<class T, class Compare>
class PQV : public vector<T> {
Compare comp;
bool sorted;
void assureHeap() {
if(sorted) {
// Turn it back into a heap:
make_heap(this->begin(),this->end(), comp);
sorted = false;
}
}
public:
PQV(Compare cmp = Compare()) : comp(cmp) {
make_heap(this->begin(),this->end(), comp);
sorted = false;
}
const T& top() {
assureHeap();
return this->front();
}
void push(const T& x) {
assureHeap();
this->push_back(x); // Put it at the end
// Re-adjust the heap:
push_heap(this->begin(),this->end(), comp);
}
void pop() {
assureHeap();
// Move the top element to the last position:
pop_heap(this->begin(),this->end(), comp);
this->pop_back();// Remove that element
}
void sort() {
if(!sorted) {
sort_heap(this->begin(),this->end(), comp);
reverse(this->begin(),this->end());
sorted = true;
}
}
};
int main() {
PQV< int, less<int> > pqi;
srand(time(0));
for(int i = 0; i < 100; i++) {
pqi.push(rand() % 25);
copy(pqi.begin(), pqi.end(),
ostream_iterator<int>(cout, "
"));
cout << "\n-----” << endl;
}
pqi.sort();
copy(pqi.begin(), pqi.end(),
ostream_iterator<int>(cout, " "));
cout << "\n-----” << endl;
while(!pqi.empty()) {
cout << pqi.top() << ' ';
pqi.pop();
}
} ///:~If sorted is true, the vector is not organized as a heap but instead as a sorted sequence. The assureHeap( ) function guarantees that it's put back into heap form before performing any heap operations on it. The first for loop in main( ) now has the additional quality that it displays the heap as it is being built.
In the previous two programs we had to introduce a seemingly extraneous usage of the “this->” prefix. Although some compilers do not require it, the standard definition of C++ does. Note that the class PQV derives from vector<T>, therefore begin( ) and end( ), inherited from vector<T>, are dependent names.(110) Compilers can't look up names from dependent base classes in the definition of a template (vector, in this case) because for a given instantiation an explicitly specialized version of the template might be used that does not have a given member. The special naming requirement guarantees that you won't end up calling a base class member in some cases and possibly a function from an enclosing scope (such as a global one) in other cases. The compiler has no way of knowing that a call to begin( ) is dependent, so we must give it a clue with a “this‑>” qualification.(111) This tells the compiler that begin( ) is in the scope of PQV, so it waits until an instance of PQV is fully instantiated. If this qualifying prefix is left out, the compiler will attempt an early lookup for the names begin and end (at template definition time, and will fail to find them because there are no such names declared in enclosing lexical scopes in this example). In the code above, however, the compiler waits until the point of instantiation of pqi, and then finds the correct specializations of begin( ) and end( ) in vector<int>.
The only drawback to this solution is that the user must remember to call sort( ) before viewing it as a sorted sequence (although one could conceivably redefine all the member functions that produce iterators so that they guarantee sorting). Another solution is to create a priority queue that is not a vector, but will build you a vector whenever you want one:
//: C07:PriorityQueue7.cpp
// A priority queue that will hand you a vector.
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <iterator>
#include <queue>
#include <vector>
using namespace std;
template<class T, class Compare> class PQV {
vector<T> v;
Compare comp;
public:
// Don't need to call make_heap(); it's empty:
PQV(Compare cmp = Compare()) : comp(cmp) {}
void push(const T& x) {
v.push_back(x); // Put it at the end
// Re-adjust the heap:
push_heap(v.begin(), v.end(), comp);
}
void pop() {
// Move the top element to the last position:
pop_heap(v.begin(), v.end(), comp);
v.pop_back(); // Remove that element
}
const T& top() { return v.front(); }
bool empty() const { return v.empty(); }
int size() const { return v.size(); }
typedef vector<T> TVec;
TVec getVector() {
TVec r(v.begin(), v.end());
// It's already a heap
sort_heap(r.begin(), r.end(), comp);
// Put it into priority-queue order:
reverse(r.begin(), r.end());
return r;
}
};
int main() {
PQV<int, less<int> > pqi;
srand(time(0));
for(int i = 0; i < 100; i++)
pqi.push(rand() % 25);
const vector<int>& v = pqi.getVector();
copy(v.begin(), v.end(),
ostream_iterator<int>(cout, " "));
cout << "\n-----------” << endl;
while(!pqi.empty()) {
cout << pqi.top() << ' ';
pqi.pop();
}
} ///:~The PQV class template follows the same form as the STL's priority_queue, but has the additional member getVector( ), which creates a new vector that's a copy of the one in PQV (which means that it's already a heap). It then sorts that copy (leaving PQV's vector untouched), and reverses the order so that traversing the new vector produces the same effect as popping the elements from the priority queue.
You may observe that the approach of deriving from priority_queue used in PriorityQueue4.cpp could be used with the above technique to produce more succinct code:
//: C07:PriorityQueue8.cpp
// A more compact version of PriorityQueue7.cpp.
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <iterator>
#include <queue>
using namespace std;
template<class T> class PQV : public
priority_queue<T> {
public:
typedef vector<T> TVec;
TVec getVector() {
TVec r(this->c.begin(),this->c.end());
// c is already a heap
sort_heap(r.begin(), r.end(), this->comp);
// Put it into priority-queue order:
reverse(r.begin(), r.end());
return r;
}
};
int main() {
PQV<int> pqi;
srand(time(0));
for(int i = 0; i < 100; i++)
pqi.push(rand() % 25);
const vector<int>& v = pqi.getVector();
copy(v.begin(), v.end(),
ostream_iterator<int>(cout, " "));
cout << "\n-----------” << endl;
while(!pqi.empty()) {
cout << pqi.top() << ' ';
pqi.pop();
}
} ///:~The brevity of this solution makes it the simplest and most desirable, plus it's guaranteed that the user will not have a vector in the unsorted state. The only potential problem is that the getVector( ) member function returns the vector<T> by value, which might cause some overhead issues with complex values of the parameter type T.
2-5-9. Holding bits▲
Because C is a language that purports to be “close to the hardware,” many have found it dismaying that there is no native binary representation for numbers. Decimal, of course, and hexadecimal (tolerable only because it's easier to group the bits in your mind), but octal? Ugh. Whenever you read specs for chips you're trying to program, they don't describe the chip registers in octal or even hexadecimal—they use binary. And yet C won't let you say 0b0101101, which is the obvious solution for a language close to the hardware.
Although there's still no native binary representation in C++, things have improved with the addition of two classes: bitset and vector<bool>, both of which are designed to manipulate a group of on-off values.(112) The primary differences between these types are:
- Each bitset holds a fixed number of bits. You establish the quantity of bits in the bitset template argument. The vector<bool> can, like a regular vector, expand dynamically to hold any number of bool values.
- The bitset template is explicitly designed for performance when manipulating bits, and is not a “regular” STL container. As such, it has no iterators. The number of bits, being a template parameter, is known at compile time and allows the underlying integral array to be stored on the runtime stack. The vector<bool> container, on the other hand, is a specialization of a vector and so has all the operations of a normal vector—the specialization is just designed to be space efficient for bool.
There is no trivial conversion between a bitset and a vector<bool>, which implies that the two are for very different purposes. Furthermore, neither is a traditional “STL container.” The bitset template class has an interface for bit-level operations and in no way resembles the STL containers we've discussed up to this point. The vector<bool> specialization of vector is similar to an STL-like container, but it differs as discussed below.
2-5-9-1. bitset<n>▲
The template for bitset accepts an unsigned integral template argument that is the number of bits to represent. Thus, bitset<10> is a different type than bitset<20>, and you cannot perform comparisons, assignments, and so on between the two.
A bitset provides the most commonly used bitwise operations in an efficient form. However, each bitset is implemented by logically packing bits in an array of integral types (typically unsignedlongs, which contain at least 32 bits). In addition, the only conversion from a bitset to a numerical value is to an unsigned long (via the function to_ulong( )).
The following example tests almost all the functionality of the bitset (the missing operations are redundant or trivial).You'll see the description of each of the bitset outputs to the right of the output so that the bits all line up and you can compare them to the source values. If you still don't understand bitwise operations, running this program should help.
//: C07:BitSet.cpp {-bor}
// Exercising the bitset class.
#include <bitset>
#include <climits>
#include <cstdlib>
#include <ctime>
#include <cstddef>
#include <iostream>
#include <string>
using namespace std;
const int SZ = 32;
typedef bitset<SZ> BS;
template<int bits> bitset<bits>
randBitset() {
bitset<bits> r(rand());
for(int i = 0; i < bits/16 - 1; i++) {
r <<= 16;
// "OR" together with a new lower 16
bits:
r |= bitset<bits>(rand());
}
return r;
}
int main() {
srand(time(0));
cout << "sizeof(bitset<16>) = "
<< sizeof(bitset<16>) << endl;
cout << "sizeof(bitset<32>) = "
<< sizeof(bitset<32>) << endl;
cout << "sizeof(bitset<48>) = "
<< sizeof(bitset<48>) << endl;
cout << "sizeof(bitset<64>) = "
<< sizeof(bitset<64>) << endl;
cout << "sizeof(bitset<65>) = "
<< sizeof(bitset<65>) << endl;
BS a(randBitset<SZ>()), b(randBitset<SZ>());
// Converting from a bitset:
unsigned long ul = a.to_ulong();
cout << a << endl;
// Converting a string to a bitset:
string cbits("111011010110111");
cout << "as a string = " <<
cbits <<endl;
cout << BS(cbits) << "
[BS(cbits)]" << endl;
cout << BS(cbits, 2) << " [BS(cbits,
2)]" << endl;
cout << BS(cbits, 2, 11) << " [BS(cbits,
2, 11)]"<< endl;
cout << a << " [a]" <<
endl;
cout << b << " [b]" <<
endl;
// Bitwise AND:
cout << (a & b) << " [a &
b]" << endl;
cout << (BS(a) &= b) << " [a
&= b]" << endl;
// Bitwise OR:
cout << (a | b) << " [a | b]"
<< endl;
cout << (BS(a) |= b) << " [a |=
b]" << endl;
// Exclusive OR:
cout << (a ^ b) << " [a ^ b]"
<< endl;
cout << (BS(a) ^= b) << " [a ^=
b]" << endl;
cout << a << " [a]" <<
endl; // For reference
// Logical left shift (fill with zeros):
cout << (BS(a) <<= SZ/2) << "
[a <<= (SZ/2)]" << endl;
cout << (a << SZ/2) << endl;
cout << a << " [a]" <<
endl; // For reference
// Logical right shift (fill with zeros):
cout << (BS(a) >>= SZ/2) << "
[a >>= (SZ/2)]" << endl;
cout << (a >> SZ/2) << endl;
cout << a << " [a]" <<
endl; // For reference
cout << BS(a).set() << "
[a.set()]" << endl;
for(int i = 0; i < SZ; i++)
if(!a.test(i)) {
cout << BS(a).set(i)
<< " [a.set(" << i
<<")]" << endl;
break; // Just do one example of this
}
cout << BS(a).reset() << "
[a.reset()]"<< endl;
for(int j = 0; j < SZ; j++)
if(a.test(j)) {
cout << BS(a).reset(j)
<< " [a.reset(" << j
<<")]" << endl;
break; // Just do one example of this
}
cout << BS(a).flip() << "
[a.flip()]" << endl;
cout << ~a << " [~a]" <<
endl;
cout << a << " [a]" <<
endl; // For reference
cout << BS(a).flip(1) << "
[a.flip(1)]"<< endl;
BS c;
cout << c << " [c]" <<
endl;
cout << "c.count() = " <<
c.count() << endl;
cout << "c.any() = "
<< (c.any() ? "true" :
"false") << endl;
cout << "c.none() = "
<< (c.none() ? "true" :
"false") << endl;
c[1].flip(); c[2].flip();
cout << c << " [c]" <<
endl;
cout << "c.count() = " <<
c.count() << endl;
cout << "c.any() = "
<< (c.any() ? "true" :
"false") << endl;
cout << "c.none() = "
<< (c.none() ? "true" :
"false") << endl;
// Array indexing operations:
c.reset();
for(size_t k = 0; k < c.size(); k++)
if(k % 2 == 0)
c[k].flip();
cout << c << " [c]" <<
endl;
c.reset();
// Assignment to bool:
for(size_t ii = 0; ii < c.size(); ii++)
c[ii] = (rand() % 100) < 25;
cout << c << " [c]" <<
endl;
// bool test:
if(c[1])
cout << "c[1] == true";
else
cout << "c[1] == false" <<
endl;
} ///:~To generate interesting random bitsets, the randBitset( ) function is created. This function demonstrates operator<<= by shifting each 16 random bits to the left until the bitset (which is templatized in this function for size) is full. The generated number and each new 16 bits are combined using the operator|=.
The main( ) function first shows the unit size of a bitset. If it is less than 32 bits, sizeof produces 4 (4 bytes = 32 bits), which is the size of a single long on most implementations. If it's between 32 and 64, it requires two longs, greater than 64 requires 3 longs, and so on. Thus, you make the best use of space if you use a bit quantity that fits in an integral number of longs. However, notice there's no extra overhead for the object—it's as if you were hand-coding for a long.
Although there are no other numerical conversions from bitset besides to_ulong( ), there is a stream inserter that produces a string containing ones and zeros, and this can be as long as the actual bitset.
There's still no primitive format for binary values, but bitset supports the next best thing: a string of ones and zeros with the least-significant bit (lsb) on the right. The three constructors demonstrated take the entire string, the string starting at character 2, and the string from character 2 through 11. You can write to an ostream from a bitset using operator<<,and it comes out as ones and zeros. You can also read from an istream using operator>> (not shown here).
You'll notice that bitset only has three nonmember operators: and (&), or (|), and exclusive-or (^). Each of these creates a new bitset as its return value. All the member operators opt for the more efficient &=, |=, and so on, where a temporary is not created. However, these forms change the bitset's value (which is a in most of the tests in the above example). To prevent this, we created a temporary to be used as the lvalue by invoking the copy-constructor on a; this is why you see the form BS(a). The result of each test is displayed, and occasionally a is reprinted so you can easily look at it for reference.
The rest of the example should be self-explanatory when you run it; if not you can find the details in your compiler's documentation or in the other documentation mentioned earlier in this chapter.
2-5-9-2. vector<bool>▲
The vector<bool> container is a specialization of the vector template. A normal bool variable requires at least one byte, but since a bool only has two states, the ideal implementation of vector<bool> is such that each bool value only requires one bit. Since typical library implementations pack the bits into integral arrays, the iterator must be specially defined and cannot be a pointer to bool.
The bit-manipulation functions for vector<bool> are much more limited than those of bitset. The only member function that was added to those already in vector is flip( ), to invert all the bits. There is no set( ) or reset( ) as in bitset. When you use operator[ ], you get back an object of type vector<bool>::reference, which also has a flip( ) to invert that individual bit.
//: C07:VectorOfBool.cpp
// Demonstrate the vector<bool> specialization.
#include <bitset>
#include <cstddef>
#include <iostream>
#include <iterator>
#include <sstream>
#include <vector>
using namespace std;
int main() {
vector<bool> vb(10, true);
vector<bool>::iterator it;
for(it = vb.begin(); it != vb.end(); it++)
cout << *it;
cout << endl;
vb.push_back(false);
ostream_iterator<bool> out(cout, "");
copy(vb.begin(), vb.end(), out);
cout << endl;
bool ab[] = { true, false, false, true, true,
true, true, false, false, true };
// There's a similar constructor:
vb.assign(ab, ab + sizeof(ab)/sizeof(bool));
copy(vb.begin(), vb.end(), out);
cout << endl;
vb.flip(); // Flip all bits
copy(vb.begin(), vb.end(), out);
cout << endl;
for(size_t i = 0; i < vb.size(); i++)
vb[i] = 0; // (Equivalent to "false")
vb[4] = true;
vb[5] = 1;
vb[7].flip(); // Invert one bit
copy(vb.begin(), vb.end(), out);
cout << endl;
// Convert to a bitset:
ostringstream os;
copy(vb.begin(), vb.end(),
ostream_iterator<bool>(os, ""));
bitset<10> bs(os.str());
cout << "Bitset:” << endl <<
bs << endl;
} ///:~The last part of this example takes a vector<bool> and converts it to a bitset by first turning it into a string of ones and zeros. Here, you must know the size of the bitset at compile time. You can see that this conversion is not the kind of operation you'll want to do on a regular basis.
The vector<bool> specialization is a “crippled” STL container in the sense that certain guarantees that other containers provide are missing. For example, with the other containers the following relationships hold:
// Let c be an STL container other than
vector<bool>:
T& r = c.front();
T* p = &*c.begin();For all other containers, the front( ) function yields an lvalue (something you can get a non-const reference to), and begin( ) must yield something you can dereference and then take the address of. Neither is possible because bits are not addressable. Both vector<bool> and bitset use a proxy class (the nested reference class, mentioned earlier) to read and set bits as necessary.
2-5-10. Associative containers▲
The set, map, multiset, and multimap are called associative containers because they associate keys with values. Well, at least maps and multimaps associate keys with values, but you can look at a set as a map that has no values, only keys (and they can in fact be implemented this way), and the same for the relationship between multiset and multimap. So, because of the structural similarity, sets and multisets are lumped in with associative containers.
The most important basic operations with associative containers are putting things in and, in the case of a set, seeing if something is in the set. In the case of a map, you want to first see if a key is in the map, and if it exists, you want the associated value for that key. There are many variations on this theme, but that's the fundamental concept. The following example shows these basics:
//: C07:AssociativeBasics.cpp {-bor}
// Basic operations with sets and maps.
//{L} Noisy
#include <cstddef>
#include <iostream>
#include <iterator>
#include <map>
#include <set>
#include "Noisy.h"
using namespace std;
int main() {
Noisy na[7];
// Add elements via constructor:
set<Noisy> ns(na, na + sizeof
na/sizeof(Noisy));
Noisy n;
ns.insert(n); // Ordinary insertion
cout << endl;
// Check for set membership:
cout << "ns.count(n)= " <<
ns.count(n) << endl;
if(ns.find(n) != ns.end())
cout << "n(" << n <<
") found in ns" << endl;
// Print elements:
copy(ns.begin(), ns.end(),
ostream_iterator<Noisy>(cout, "
"));
cout << endl;
cout << "\n-----------” << endl;
map<int, Noisy> nm;
for(int i = 0; i < 10; i++)
nm[i]; // Automatically makes pairs
cout << "\n-----------” << endl;
for(size_t j = 0; j < nm.size(); j++)
cout << "nm[" << j
<<"] = " << nm[j] << endl;
cout << "\n-----------” << endl;
nm[10] = n;
cout << "\n-----------” << endl;
nm.insert(make_pair(47, n));
cout << "\n-----------” << endl;
cout << "\n nm.count(10)= " <<
nm.count(10) << endl;
cout << "nm.count(11)= " <<
nm.count(11) << endl;
map<int, Noisy>::iterator it = nm.find(6);
if(it != nm.end())
cout << "value:" <<
(*it).second
<< " found in nm at location
6" << endl;
for(it = nm.begin(); it != nm.end(); it++)
cout << (*it).first << ":"
<< (*it).second << ", ";
cout << "\n-----------” << endl;
} ///:~The set<Noisy> object ns is created using two iterators into an array of Noisy objects, but there is also a default constructor and a copy-constructor, and you can pass in an object that provides an alternate scheme for doing comparisons. Both sets and maps have an insert( ) member function to put things in, and you can check to see if an object is already in an associative container in two ways. The count( ) member function, when given a key, will tell you how many times that key occurs. (This can only be zero or one in a set or map, but it can be more than one with a multiset or multimap.) The find( ) member function will produce an iterator indicating the first occurrence (with set and map, the only occurrence) of the key that you give it or will produce the past-the-end iterator if it can't find the key. The count( ) and find( ) member functions exist for all the associative containers, which makes sense. The associative containers also have member functions lower_bound( ), upper_bound( ), and equal_range( ), which only make sense for multiset and multimap, as you will see. (But don't try to figure out how they would be useful for set and map, since they are designed for dealing with a range of duplicate keys, which those containers don't allow.)
Designing an operator[ ] always presents a bit of a dilemma. Because it's intended to be treated as an array-indexing operation, people don't tend to think about performing a test before they use it. But what happens if you decide to index out of the bounds of the array? One option is to throw an exception, but with a map, “indexing out of the array” could mean that you want to create a new entry at that location, and that's the way the STL map treats it. The first for loop after the creation of the map<int, Noisy> nm just “looks up” objects using the operator[ ], but this is actually creating new Noisy objects! The map creates a new key-value pair (using the default constructor for the value) if you look up a value with operator[ ] and it isn't there. This means that if you really just want to look something up and not create a new entry, you must use the member functions count( ) (to see if it's there) or find( ) (to get an iterator to it).
A number of problems are associated with the for loop that prints the values of the container using operator[ ]. First, it requires integral keys (which we happen to have here). Next and worse, if all the keys are not sequential, you'll end up counting from zero to the size of the container, and if some spots don't have key-value pairs, you'll automatically create them and miss some of the higher values of the keys. Finally, if you look at the output from the for loop, you'll see that things are very busy, and it's quite puzzling at first why there are so many constructions and destructions for what appears to be a simple lookup. The answer only becomes clear when you look at the code in the map template for operator[ ], which will be something like this:
mapped_type& operator[] (const key_type& k) {
value_type tmp(k,T());
return (*((insert(tmp)).first)).second;
}The map::insert( ) function takes a key-value pair and does nothing if there is already an entry in the map with the given key—otherwise it inserts an entry for the key. In either case, it returns a new key-value pair holding an iterator to the inserted pair as its first element and holding true as the second element if an insertion took place. The members first and second give the key and value, respectively, because map::value_type is really just a typedef for a std::pair:
typedef pair<const Key, T> value_type;You've seen the std::pair template before. It's a simple holder for two values of independent types, as you can see by its definition:
template<class T1, class T2> struct pair {
typedef T1 first_type;
typedef T2 second_type;
T1 first;
T2 second;
pair();
pair(const T1& x, const T2& y) : first(x),
second(y) {}
// Templatized copy-constructor:
template<class U, class V> pair(const
pair<U, V> &p);
};The pair template class is very useful, especially when you want to return two objects from a function (since a return statement only takes one object). There's even a shorthand for creating a pair called make_pair( ), which is used in AssociativeBasics.cpp.
So to retrace the steps, map::value_type is a pair of the key and the value of the map—actually, it's a single entry for the map. But notice that pair packages its objects by value, which means that copy-constructions are necessary to get the objects into the pair. Thus, the creation of tmp in map::operator[ ] will involve at least a copy-constructor call and destructor call for each object in the pair. Here, we're getting off easy because the key is an int. But if you want to really see what kind of activity can result from map::operator[ ], try running this:
//: C07:NoisyMap.cpp
// Mapping Noisy to Noisy.
//{L} Noisy
#include <map>
#include "Noisy.h"
using namespace std;
int main() {
map<Noisy, Noisy> mnn;
Noisy n1, n2;
cout << "\n--------” << endl;
mnn[n1] = n2;
cout << "\n--------” << endl;
cout << mnn[n1] << endl;
cout << "\n--------” << endl;
} ///:~You'll see that both the insertion and lookup generate a lot of extra objects, and that's because of the creation of the tmp object. If you look back up at map::operator[ ], you'll see that the second line calls insert( ), passing it tmp—that is, operator[ ] does an insertion every time. The return value of insert( ) is a different kind of pair, where first is an iterator pointing to the key-value pair that was just inserted, and second is a bool indicating whether the insertion took place. You can see that operator[ ] grabs first (the iterator), dereferences it to produce the pair, and then returns the second, which is the value at that location.
So on the upside, map has this fancy “make a new entry if one isn't there” behavior, but the downside is that you always get a lot of extra object creations and destructions when you use map::operator[ ]. Fortunately, AssociativeBasics.cpp also demonstrates how to reduce the overhead of insertions and deletions, by avoiding operator[ ] if you don't need it. The insert( ) member function is slightly more efficient than operator[ ]. With a set, you hold only one object, but with a map, you hold key-value pairs; so insert( ) requires a pair as its argument. Here's where make_pair( ) comes in handy, as you can see.
For looking objects up in a map, you can use count( ) to see whether a key is in the map, or you can use find( ) to produce an iterator pointing directly at the key-value pair. Again, since the map contains pairs, that's what the iterator produces when you dereference it, so you have to select first and second. When you run AssociativeBasics.cpp, you'll notice that the iterator approach involves no extra object creations or destructions. It's not as easy to write or read, though.
2-5-10-1. Generators and fillers for associative containers▲
You've seen how useful the fill( ), fill_n( ), generate( ), and generate_n( ) function templates in <algorithm> have been for filling the sequential containers (vector, list, and deque) with data. However, these are implemented by using operator= to assign values into the sequential containers, and the way that you add objects to associative containers is with their respective insert( ) member functions. Thus, the default “assignment” behavior causes a problem when trying to use the “fill” and “generate” functions with associative containers.
One solution is to duplicate the “fill” and “generate” functions, creating new ones that can be used with associative containers. It turns out that only the fill_n( ) and generate_n( ) functions can be duplicated (fill( ) and generate( ) copy sequences, which doesn't make sense with associative containers), but the job is fairly easy, since you have the <algorithm> header file to work from:
//: C07:assocGen.h
// The fill_n() and generate_n() equivalents
// for associative containers.
#ifndef ASSOCGEN_H
#define ASSOCGEN_H
template<class Assoc, class Count, class T>
void assocFill_n(Assoc& a, Count n, const T&
val) {
while(n-- > 0)
a.insert(val);
}
template<class Assoc, class Count, class Gen>
void assocGen_n(Assoc& a, Count n, Gen g) {
while(n-- > 0)
a.insert(g());
}
#endif // ASSOCGEN_H ///:~You can see that instead of using iterators, the container class itself is passed (by reference, of course).
This code demonstrates two valuable lessons. The first is that if the algorithms don't do what you want, copy the nearest thing and modify it. You have the example at hand in the STL header, so most of the work has already been done.
The second lesson is more pointed: if you look long enough, there's probably a way to do it in the STL without inventing anything new. The present problem can instead be solved by using an insert_iterator (produced by a call to inserter( )), which calls insert( ) to place items in the container instead of operator=. This is not simply a variation of front_insert_iterator or back_insert_iterator because those iterators use push_front( ) and push_back( ), respectively. Each of the insert iterators is different by virtue of the member function it uses for insertion, and insert( ) is the one we need. Here's a demonstration that shows filling and generating both a map and a set. (It can also be used with multimap and multiset.) First, some templatized generators are created. (This may seem like overkill, but you never know when you'll need them. For that reason they're placed in a header file.)
//: C07:SimpleGenerators.h
// Generic generators, including one that creates pairs.
#include <iostream>
#include <utility>
// A generator that increments its value:
template<typename T> class IncrGen {
T i;
public:
IncrGen(T ii) : i(ii) {}
T operator()() { return i++; }
};
// A generator that produces an STL pair<>:
template<typename T1, typename T2> class PairGen
{
T1 i;
T2 j;
public:
PairGen(T1 ii, T2 jj) : i(ii), j(jj) {}
std::pair<T1,T2> operator()() {
return std::pair<T1,T2>(i++, j++);
}
};
namespace std {
// A generic global operator<< for printing any
STL pair<>:
template<typename F, typename S> ostream&
operator<<(ostream& os, const
pair<F,S>& p) {
return os << p.first << "\t"
<< p.second << endl;
}
} ///:~Both generators expect that T can be incremented, and they simply use operator++ to generate new values from whatever you used for initialization. PairGen creates an STL pair object as its return value, and that's what can be placed into a map or multimap using insert( ).
The last function is a generalization of operator<< for ostreams, so that any pair can be printed, assuming each element of the pair supports a stream operator<<. (It is in namespace std for the strange name lookup reasons discussed in Chapter 5, and explained once again after Thesaurus.cpp later on in this chapter.) As you can see in the following, this allows the use of copy( ) to output the map:
//: C07:AssocInserter.cpp
// Using an insert_iterator so fill_n() and generate_n()
// can be used with associative containers.
#include <iterator>
#include <iostream>
#include <algorithm>
#include <set>
#include <map>
#include "SimpleGenerators.h"
using namespace std;
int main() {
set<int> s;
fill_n(inserter(s, s.begin()), 10, 47);
generate_n(inserter(s, s.begin()), 10,
IncrGen<int>(12));
copy(s.begin(), s.end(),
ostream_iterator<int>(cout, "\n"));
map<int, int> m;
fill_n(inserter(m, m.begin()), 10,
make_pair(90,120));
generate_n(inserter(m, m.begin()), 10,
PairGen<int, int>(3, 9));
copy(m.begin(), m.end(),
ostream_iterator<pair<int,int>
>(cout,"\n"));
} ///:~The second argument to inserter is an iterator, which is an optimization hint to help the insertion go faster (instead of always starting the search at the root of the underlying tree). Since an insert_iterator can be used with many different types of containers, with non-associative containers it is more than a hint—it is required.
Note how the ostream_iterator is created to output a pair. This won't work if the operator<< isn't created. Since it's a template, it is automatically instantiated for pair<int, int>.
2-5-10-2. The magic of maps▲
An ordinary array uses an integral value to index into a sequential set of elements of some type. A map is an associative array, which means you associate one object with another in an array-like fashion. Instead of selecting an array element with a number as you do with an ordinary array, you look it up with an object! The example that follows counts the words in a text file, so the index is the string object representing the word, and the value being looked up is the object that keeps count of the strings.
In a single-item container such as a vector or a list, only one thing is being held. But in a map, you've got two things: the key (what you look up by, as in mapname[key]) and the value that results from the lookup with the key. If you simply want to move through the entire map and list each key-value pair, you use an iterator, which when dereferenced produces a pair object containing both the key and the value. You access the members of a pair by selecting first or second.
This same philosophy of packaging two items together is also used to insert elements into the map, but the pair is created as part of the instantiated map and is called value_type, containing the key and the value. So one option for inserting a new element is to create a value_type object, loading it with the appropriate objects and then calling the insert( ) member function for the map. Instead, the following example uses the aforementioned special feature of map: if you're trying to find an object by passing in a key to operator[ ] and that object doesn't exist, operator[ ] will automatically insert a new key-value pair for you, using the default constructor for the value object. With that in mind, consider an implementation of a word-counting program:
//: C07:WordCount.cpp
// Count occurrences of words using a map.
#include <iostream>
#include <fstream>
#include <map>
#include <string>
#include "../require.h"
using namespace std;
int main(int argc, char* argv[]) {
typedef map<string, int> WordMap;
typedef WordMap::iterator WMIter;
const char* fname = "WordCount.cpp";
if(argc > 1) fname = argv[1];
ifstream in(fname);
assure(in, fname);
WordMap wordmap;
string word;
while(in >> word)
wordmap[word]++;
for(WMIter w = wordmap.begin(); w != wordmap.end();
w++)
cout << w->first << ": "
<< w->second << endl;
} ///:~This example shows the power of zero-initialization. Consider this line of code from the program:
wordmap[word]++;This expression increments the int associated with word. If there isn't such a word in the map, a key-value pair for the word is automatically inserted, with the value initialized to zero by a call to the pseudo-constructor int( ), which returns a 0.
Printing the entire list requires traversing it with an iterator. (There's no copy( ) shortcut for a map unless you want to write an operator<< for the pair in the map.) As previously mentioned, dereferencing this iterator produces a pair object, with the first member the key and the second member the value.
If you want to find the count for a particular word, you can use the array index operator, like this:
cout << "the: " << wordmap["the"] <<
endl;You can see that one of the great advantages of the map is the clarity of the syntax; an associative array makes intuitive sense to the reader. (Note, however, that if “the” isn't already in the wordmap, a new entry will be created!)
2-5-10-3. Multimaps and duplicate keys▲
A multimap is a map that can contain duplicate keys. At first this may seem like a strange idea, but it can occur surprisingly often. A phone book, for example, can have many entries with the same name.
Suppose you are monitoring wildlife, and you want to keep track of where and when each type of animal is spotted. Thus, you may see many animals of the same kind, all in different locations and at different times. So if the type of animal is the key, you'll need a multimap. Here's what it looks like:
//: C07:WildLifeMonitor.cpp
#include <algorithm>
#include <cstdlib>
#include <cstddef>
#include <ctime>
#include <iostream>
#include <iterator>
#include <map>
#include <sstream>
#include <string>
#include <vector>
using namespace std;
class DataPoint {
int x, y; // Location coordinates
time_t time; // Time of Sighting
public:
DataPoint() : x(0), y(0), time(0) {}
DataPoint(int xx, int yy, time_t tm) :
x(xx), y(yy), time(tm) {}
// Synthesized operator=, copy-constructor OK
int getX() const { return x; }
int getY() const { return y; }
const time_t* getTime() const { return &time; }
};
string animal[] = {
"chipmunk", "beaver",
"marmot", "weasel",
"squirrel", "ptarmigan",
"bear", "eagle",
"hawk", "vole", "deer",
"otter", "hummingbird",
};
const int ASZ = sizeof animal/sizeof *animal;
vector<string> animals(animal, animal + ASZ);
// All the information is contained in a
// "Sighting," which can be sent to an
ostream:
typedef pair<string, DataPoint> Sighting;
ostream&
operator<<(ostream& os, const Sighting&
s) {
return os << s.first << " sighted at
x= "
<< s.second.getX() << ", y= "
<< s.second.getY()
<< ", time = " <<
ctime(s.second.getTime());
}
// A generator for Sightings:
class SightingGen {
vector<string>& animals;
enum { D = 100 };
public:
SightingGen(vector<string>& an) :
animals(an) {}
Sighting operator()() {
Sighting result;
int select = rand() % animals.size();
result.first = animals[select];
result.second = DataPoint(
rand() % D, rand() % D, time(0));
return result;
}
};
// Display a menu of animals, allow the user to
// select one, return the index value:
int menu() {
cout << "select an animal or 'q' to quit:
";
for(size_t i = 0; i < animals.size(); i++)
cout <<'['<< i <<']'<<
animals[i] << ' ';
cout << endl;
string reply;
cin >> reply;
if(reply.at(0) == 'q') return 0;
istringstream r(reply);
int i;
r >> i; // Converts to int
i %= animals.size();
return i;
}
int main() {
typedef multimap<string, DataPoint> DataMap;
typedef DataMap::iterator DMIter;
DataMap sightings;
srand(time(0)); // Randomize
generate_n(inserter(sightings, sightings.begin()),
50, SightingGen(animals));
// Print everything:
copy(sightings.begin(), sightings.end(),
ostream_iterator<Sighting>(cout,
""));
// Print sightings for selected animal:
for(int count = 1; count < 10; count++) {
// Use menu to get selection:
// int i = menu();
// Generate randomly (for automated testing):
int i = rand() % animals.size();
// Iterators in "range" denote begin, one
// past end of matching range:
pair<DMIter, DMIter> range =
sightings.equal_range(animals[i]);
copy(range.first, range.second,
ostream_iterator<Sighting>(cout,
""));
}
} ///:~All the data about a sighting is encapsulated into the class DataPoint, which is simple enough that it can rely on the synthesized assignment and copy-constructor. It uses the Standard C library time functions to record the time of the sighting.
In the array of string, animal, notice that the char* constructor is automatically used during initialization, which makes initializing an array of string quite convenient. Since it's easier to use the animal names in a vector, the length of the array is calculated, and a vector<string> is initialized using the vector(iterator, iterator) constructor.
The key-value pairs that make up a Sighting are the string, which names the type of animal, and the DataPoint, which says where and when it was sighted. The standard pair template combines these two types and is typedefed to produce the Sighting type. Then an ostream operator<< is created for Sighting; this will allow you to iterate through a map or multimap of Sightingsand display it.
SightingGen generates random sightings at random data points to use for testing. It has the usual operator( ) necessary for a function object, but it also has a constructor to capture and store a reference to a vector<string>, which is where the aforementioned animal names are stored.
A DataMap is a multimap of string-DataPoint pairs, which means it stores Sightings. It is filled with 50 Sightings using generate_n( ) and displayed. (Notice that because there is an operator<< that takes a Sighting, an ostream_iterator can be created.) At this point the user is asked to select the animal for which they want to see all the sightings. If you press q, the program will quit, but if you select an animal number, the equal_range( ) member function is invoked. This returns an iterator (DMIter) to the beginning of the set of matching pairs and an iterator indicating past-the-end of the set. Since only one object can be returned from a function, equal_range( ) makes use of pair. Since the range pair has the beginning and ending iterators of the matching set, those iterators can be used in copy( ) to print all the sightings for a particular type of animal.
2-5-10-4. Multisets▲
You've seen the set, which allows only one object of each value to be inserted. The multiset is odd by comparison since it allows more than one object of each value to be inserted. This seems to go against the whole idea of “setness,” where you can ask, “Is ‘it' in this set?” If there can be more than one “it,” what does that question mean?
With some thought, you can see that it makes little sense to have more than one object of the same value in a set if those duplicate objects are exactly the same (with the possible exception of counting occurrences of objects, but as seen earlier in this chapter that can be handled in an alternative, more elegant fashion). Thus, each duplicate object will have something that makes it “different” from the other duplicates—most likely different state information that is not used in the calculation of the key during the comparison. That is, to the comparison operation, the objects look the same, but they contain some differing internal state.
Like any STL container that must order its elements, the multiset template uses the less function object by default to determine element ordering. This uses the contained class's operator<, but you can always substitute your own comparison function.
Consider a simple class that contains one element that is used in the comparison and another that is not:
//: C07:MultiSet1.cpp
// Demonstration of multiset behavior.
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <iterator>
#include <set>
using namespace std;
class X {
char c; // Used in comparison
int i; // Not used in comparison
// Don't need default constructor and operator=
X();
X& operator=(const X&);
// Usually need a copy-constructor (but the
// synthesized version works here)
public:
X(char cc, int ii) : c(cc), i(ii) {}
// Notice no operator== is
required
friend bool operator<(const X& x, const X&
y) {
return x.c < y.c;
}
friend ostream& operator<<(ostream& os,
X x) {
return os << x.c << ":"
<< x.i;
}
};
class Xgen {
static int i;
// Number of characters to select from:
enum { SPAN = 6 };
public:
X operator()() {
char c = 'A' + rand() % SPAN;
return X(c, i++);
}
};
int Xgen::i = 0;
typedef multiset<X> Xmset;
typedef Xmset::const_iterator Xmit;
int main() {
Xmset mset;
// Fill it with X's:
srand(time(0)); // Randomize
generate_n(inserter(mset, mset.begin()), 25, Xgen());
// Initialize a regular set from mset:
set<X> unique(mset.begin(), mset.end());
copy(unique.begin(), unique.end(),
ostream_iterator<X>(cout, " "));
cout << "\n----” << endl;
// Iterate over the unique values:
for(set<X>::iterator i = unique.begin();
i != unique.end(); i++) {
pair<Xmit, Xmit> p = mset.equal_range(*i);
copy(p.first,p.second,
ostream_iterator<X>(cout, " "));
cout << endl;
}
} ///:~In X, all the comparisons are made with the char c. The comparison is performed with operator<, which is all that is necessary for the multiset, since in this example the default less comparison object is used. The class Xgen randomly generates X objects, but the comparison value is restricted to the span from ‘A' to ‘E'. In main( ), a multiset<X> is created and filled with 25 X objects using Xgen, guaranteeing that there will be duplicate keys. So that we know what the unique values are, a regular set<X> is created from the multiset (using the iterator, iterator constructor). These values are displayed, and then each one produces the equal_range( ) in the multiset (equal_range( ) has the same meaning here as it does with multimap: all the elements with matching keys). Each set of matching keys is then printed.
As a second example, a (possibly) more elegant version of WordCount.cpp can be created using multiset:
//: C07:MultiSetWordCount.cpp
// Count occurrences of words using a multiset.
#include <fstream>
#include <iostream>
#include <iterator>
#include <set>
#include <string>
#include "../require.h"
using namespace std;
int main(int argc, char* argv[]) {
const char* fname =
"MultiSetWordCount.cpp";
if(argc > 1) fname = argv[1];
ifstream in(fname);
assure(in, fname);
multiset<string> wordmset;
string word;
while(in >> word)
wordmset.insert(word);
typedef multiset<string>::iterator MSit;
MSit it = wordmset.begin();
while(it != wordmset.end()) {
pair<MSit, MSit> p = wordmset.equal_range(*it);
int count = distance(p.first, p.second);
cout << *it << ": " <<
count << endl;
it = p.second; // Move to the next word
}
} ///:~The setup in main( ) is identical to WordCount.cpp, but then each word is simply inserted into the multiset<string>. An iterator is created and initialized to the beginning of the multiset; dereferencing this iterator produces the current word. The equal_range( ) member function (not generic algorithm) produces the starting and ending iterators of the word that's currently selected, and the algorithm distance( ) (defined in <iterator>) counts the number of elements in that range. The iterator it is then moved forward to the end of the range, which puts it at the next word. If you're unfamiliar with the multiset, this code can seem more complex. The density of it and the lack of need for supporting classes such as Count has a lot of appeal.
In the end, is this really a “set,” or should it be called something else? An alternative is the generic “bag” that is defined in some container libraries, since a bag holds anything, without discrimination—including duplicate objects. This is close, but it doesn't quite fit since a bag has no specification about how elements should be ordered. A multiset (which requires that all duplicate elements be adjacent to each other) is even more restrictive than the concept of a set. A set implementation might use a hashing function to order its elements, which would not put them in sorted order. Besides, if you want to store a bunch of objects without any special criteria, you will probably just use a vector, deque, or list.
2-5-11. Combining STL containers▲
When using a thesaurus, you want to know all the words that are similar to a particular word. When you look up a word, then, you want a list of words as the result. Here, the “multi” containers (multimap or multiset) are not appropriate. The solution is to combine containers, which is easily done using the STL. Here, we need a tool that turns out to be a powerful general concept, which is a map that associates a string with a vector:
//: C07:Thesaurus.cpp
// A map of vectors.
#include <map>
#include <vector>
#include <string>
#include <iostream>
#include <iterator>
#include <algorithm>
#include <ctime>
#include <cstdlib>
using namespace std;
typedef map<string, vector<string> >
Thesaurus;
typedef pair<string, vector<string> >
TEntry;
typedef Thesaurus::iterator TIter;
// Name lookup work-around:
namespace std {
ostream& operator<<(ostream& os,const
TEntry& t) {
os << t.first << ": ";
copy(t.second.begin(), t.second.end(),
ostream_iterator<string>(os, " "));
return os;
}
}
// A generator for thesaurus test entries:
class ThesaurusGen {
static const string letters;
static int count;
public:
int maxSize() { return letters.size(); }
TEntry operator()() {
TEntry result;
if(count >= maxSize()) count = 0;
result.first = letters[count++];
int entries = (rand() % 5) + 2;
for(int i = 0; i < entries; i++) {
int choice = rand() % maxSize();
char cbuf[2] = { 0 };
cbuf[0] = letters[choice];
result.second.push_back(cbuf);
}
return result;
}
};
int ThesaurusGen::count = 0;
const string ThesaurusGen::letters("ABCDEFGHIJKL"
"MNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz");
// Ask for a "word" to look up:
string menu(Thesaurus& thesaurus) {
while(true) {
cout << "Select a \"word\", 0
to quit: ";
for(TIter it = thesaurus.begin();
it != thesaurus.end(); it++)
cout << (*it).first << ' ';
cout << endl;
string reply;
cin >> reply;
if(reply.at(0) == '0') exit(0); // Quit
if(thesaurus.find(reply) == thesaurus.end())
continue; // Not in list, try again
return reply;
}
}
int main() {
srand(time(0)); // Seed the random number generator
Thesaurus thesaurus;
// Fill with 10 entries:
generate_n(inserter(thesaurus, thesaurus.begin()),
10, ThesaurusGen());
// Print everything:
copy(thesaurus.begin(), thesaurus.end(),
ostream_iterator<TEntry>(cout,
"\n"));
// Create a list of the keys:
string keys[10];
int i = 0;
for(TIter it = thesaurus.begin();
it != thesaurus.end(); it++)
keys[i++] = (*it).first;
for(int count = 0; count < 10; count++) {
// Enter from the console:
// string reply = menu(thesaurus);
// Generate randomly
string reply = keys[rand() % 10];
vector<string>& v = thesaurus[reply];
copy(v.begin(), v.end(),
ostream_iterator<string>(cout, "
"));
cout << endl;
}
} ///:~A Thesaurus maps a string (the word) to a vector<string> (the synonyms). A TEntry is a single entry in a Thesaurus. By creating an ostream operator<< for a TEntry, a single entry from the Thesaurus can easily be printed (and the whole Thesaurus can easily be printed with copy( )). Notice the very strange placement of the stream inserter: we put it inside the std namespace!(113) This operator<<( ) function is used by ostream_iterator in the first call to copy( ) in main( ) above. When the compiler instantiates the needed ostream_iterator specialization, according to the rules of argument-dependent lookup (ADL) it only looks in std because that is where all the arguments to copy( ) are declared. If we declared our inserter in the global namespace (by removing the namespace block around it), then it would not be found. By placing it in std we enable ADL to find it.
The ThesaurusGen creates “words” (which are just single letters) and “synonyms” for those words (which are just other randomly chosen single letters) to be used as thesaurus entries. It randomly chooses the number of synonym entries to make, but there must be at least two. All the letters are chosen by indexing into a static string that is part of ThesaurusGen.
In main( ), a Thesaurus is created, filled with 10 entries and printed using the copy( ) algorithm. The menu( ) function asks the user to choose a “word” to look up by typing the letter of that word. The find( ) member function discovers whether the entry exists in the map. (Remember, you don't want to use operator[ ], which will automatically make a new entry if it doesn't find a match!) If so, operator[ ] fetches out the vector<string> that is displayed. The selection of the reply string is generated randomly, to allow automated testing.
Because templates make the expression of powerful concepts easy, you can take this concept much further, creating a map of vectors containing maps, and so on. For that matter, you can combine any of the STL containers this way.
2-5-12. Cleaning up containers of pointers▲
In Stlshape.cpp, the pointers did not clean themselves up automatically. It would be convenient to be able to do this easily, rather than writing out the code each time. Here is a function template that will clean up the pointers in any sequence container. Note that it is placed in the book's root directory for easy access:
//: :purge.h
// Delete pointers in an STL sequence container.
#ifndef PURGE_H
#define PURGE_H
#include <algorithm>
template<class Seq> void purge(Seq& c) {
typename Seq::iterator i;
for(i = c.begin(); i != c.end(); ++i) {
delete *i;
*i = 0;
}
}
// Iterator version:
template<class InpIt> void purge(InpIt begin,
InpIt end) {
while(begin != end) {
delete *begin;
*begin = 0;
++begin;
}
}
#endif // PURGE_H ///:~In the first version of purge( ), note that typename is absolutely necessary. This is exactly the case that keyword was designed to solve: Seq is a template argument, and iterator is something that is nested within that template. So what does Seq::iterator refer to? The typename keyword specifies that it refers to a type, and not something else.
Although the container version of purge( ) must work with an STL-style container, the iterator version of purge( ) will work with any range, including an array.
Here is a rewrite of Stlshape.cpp, modified to use the purge( ) function:
//: C07:Stlshape2.cpp
// Stlshape.cpp with the purge() function.
#include <iostream>
#include <vector>
#include "../purge.h"
using namespace std;
class Shape {
public:
virtual void draw() = 0;
virtual ~Shape() {};
};
class Circle : public Shape {
public:
void draw() { cout << "Circle::draw”
<< endl; }
~Circle() { cout << "~Circle” <<
endl; }
};
class Triangle : public Shape {
public:
void draw() { cout << "Triangle::draw”
<< endl; }
~Triangle() { cout << "~Triangle” <<
endl; }
};
class Square : public Shape {
public:
void draw() { cout << "Square::draw”
<< endl; }
~Square() { cout << "~Square” <<
endl; }
};
int main() {
typedef std::vector<Shape*> Container;
typedef Container::iterator Iter;
Container shapes;
shapes.push_back(new Circle);
shapes.push_back(new Square);
shapes.push_back(new Triangle);
for(Iter i = shapes.begin(); i != shapes.end(); i++)
(*i)->draw();
purge(shapes);
} ///:~When using purge( ), carefully consider ownership issues. If an object pointer is held in more than one container, be sure not to delete it twice, and you don't want to destroy the object in the first container before the second one is finished with it. Purging the same container twice is not a problem because purge( ) sets the pointer to zero once it deletes that pointer, and calling delete for a zero pointer is a safe operation.
2-5-13. Creating your own containers▲
With the STL as a foundation, you can create your own containers. Assuming you follow the same model of providing iterators, your new container will behave as if it were a built-in STL container.
Consider the “ring” data structure, which is a circular sequence container. If you reach the end, it just wraps around to the beginning. This can be implemented on top of a list as follows:
//: C07:Ring.cpp
// Making a "ring" data structure from the
STL.
#include <iostream>
#include <iterator>
#include <list>
#include <string>
using namespace std;
template<class T> class Ring {
list<T> lst;
public:
// Declaration necessary so the following
// 'friend' statement sees this 'iterator'
// instead of std::iterator:
class iterator;
friend class iterator;
class iterator : public std::iterator<
std::bidirectional_iterator_tag,T,ptrdiff_t>{
typename list<T>::iterator it;
list<T>* r;
public:
iterator(list<T>& lst,
const typename list<T>::iterator& i)
: it(i), r(&lst) {}
bool operator==(const iterator& x) const {
return it == x.it;
}
bool operator!=(const iterator& x) const {
return !(*this == x);
}
typename list<T>::reference operator*() const
{
return *it;
}
iterator& operator++() {
++it;
if(it == r->end())
it = r->begin();
return *this;
}
iterator operator++(int) {
iterator tmp = *this;
++*this;
return tmp;
}
iterator& operator--() {
if(it == r->begin())
it = r->end();
--it;
return *this;
}
iterator operator--(int) {
iterator tmp = *this;
--*this;
return tmp;
}
iterator insert(const T& x) {
return iterator(*r, r->insert(it, x));
}
iterator erase() {
return iterator(*r, r->erase(it));
}
};
void push_back(const T& x) { lst.push_back(x); }
iterator begin() { return iterator(lst, lst.begin());
}
int size() { return lst.size(); }
};
int main() {
Ring<string> rs;
rs.push_back("one");
rs.push_back("two");
rs.push_back("three");
rs.push_back("four");
rs.push_back("five");
Ring<string>::iterator it = rs.begin();
++it; ++it;
it.insert("six");
it = rs.begin();
// Twice around the ring:
for(int i = 0; i < rs.size() * 2; i++)
cout << *it++ << endl;
} ///:~You can see that most of the coding is in the iterator. The Ringiterator must know how to loop back to the beginning, so it must keep a reference to the list ofits “parent” Ring object in order to know if it's at the end and how to get back to the beginning.
You'll notice that the interface for Ring is quite limited; in particular, there is no end( ), since a ring just keeps looping. This means that you won't be able to use a Ring in any STL algorithms that require a past-the-end iterator, which are many. (It turns out that adding this feature is a nontrivial exercise.) Although this can seem limiting, consider stack, queue, and priority_queue, which don't produce any iterators at all!
2-5-14. STL extensions▲
Although the STL containers may provide all the functionality you'll ever need, they are not complete. For example, the standard implementations of set and map use trees, and although these are reasonably fast, they may not be fast enough for your needs. In the C++ Standards Committee it was generally agreed that hashed implementations of set and map should have been included in Standard C++, however, there was not enough time to add these components, and thus they were left out.(114)
Fortunately, alternatives are freely available. One of the nice things about the STL is that it establishes a basic model for creating STL-like classes, so anything built using the same model is easy to understand if you are already familiar with the STL.
The SGI STL from Silicon Graphics(115) is one of the most robust implementations of the STL and can be used to replace your compiler's STL if that is found wanting. In addition, SGI has added a number of extensions including hash_set, hash_multiset, hash_map, hash_multimap, slist (a singly linked list), and rope (a variant of string optimized for very large strings and fast concatenation and substring operations).
Let's consider a performance comparison between a tree-based map and the SGI hash_map. To keep things simple, the mappings will be from int to int:
//: C07:MapVsHashMap.cpp
// The hash_map header is not part of the Standard C++
STL.
// It is an extension that is only available as part of
the
// SGI STL (Included with the dmc distribution).
// You can add the header by hand for all of these:
//{-bor}{-msc}{-g++}{-mwcc}
#include <hash_map>
#include <iostream>
#include <map>
#include <ctime>
using namespace std;
int main() {
hash_map<int, int> hm;
map<int, int> m;
clock_t ticks = clock();
for(int i = 0; i < 100; i++)
for(int j = 0; j < 1000; j++)
m.insert(make_pair(j,j));
cout << "map insertions: " <<
clock() - ticks << endl;
ticks = clock();
for(int i = 0; i < 100; i++)
for(int j = 0; j < 1000; j++)
hm.insert(make_pair(j,j));
cout << "hash_map insertions: "
<< clock() - ticks << endl;
ticks = clock();
for(int i = 0; i < 100; i++)
for(int j = 0; j < 1000; j++)
m[j];
cout << "map::operator[] lookups: "
<< clock() - ticks << endl;
ticks = clock();
for(int i = 0; i < 100; i++)
for(int j = 0; j < 1000; j++)
hm[j];
cout << "hash_map::operator[] lookups:
"
<< clock() - ticks << endl;
ticks = clock();
for(int i = 0; i < 100; i++)
for(int j = 0; j < 1000; j++)
m.find(j);
cout << "map::find() lookups: "
<< clock() - ticks << endl;
ticks = clock();
for(int i = 0; i < 100; i++)
for(int j = 0; j < 1000; j++)
hm.find(j);
cout << "hash_map::find() lookups: "
<< clock() - ticks << endl;
} ///:~The performance test we ran showed a speed improvement of roughly 4: 1 for the hash_map over the map in all operations (and as expected, find( ) is slightly faster than operator[ ] for lookups for both types of map). If a profiler shows a bottleneck in your map, consider a hash_map.
2-5-15. Non-STL containers▲
There are two “non-STL” containers in the standard library: bitset and valarray.(116) We say “non-STL” because neither of these containers fulfills all the requirements of STL containers. The bitset container, which we covered earlier in this chapter, packs bits into integers and does not allow direct addressing of its members. The valarray template class is a vector-like container that is optimized for efficient numeric computation. Neither container provides iterators. Although you can instantiate a valarray with nonnumeric types, it has mathematical functions that are intended to operate with numeric data, such as sin, cos, tan, and so on.
Here's a tool to print elements in a valarray:
//: C07:PrintValarray.h
#ifndef PRINTVALARRAY_H
#define PRINTVALARRAY_H
#include <valarray>
#include <iostream>
#include <cstddef>
template<class T>
void print(const char* lbl, const
std::valarray<T>& a) {
std::cout << lbl << ": ";
for(std::size_t i = 0; i < a.size(); ++i)
std::cout << a[i] << ' ';
std::cout << std::endl;
}
#endif // PRINTVALARRAY_H ///:~Most of valarray's functions and operators operate on a valarray as a whole, as the following example illustrates:
//: C07:Valarray1.cpp {-bor}
// Illustrates basic valarray functionality.
#include "PrintValarray.h"
using namespace std;
double f(double x) { return 2.0 * x - 1.0; }
int main() {
double n[] = { 1.0, 2.0, 3.0, 4.0 };
valarray<double> v(n, sizeof n / sizeof n[0]);
print("v", v);
valarray<double> sh(v.shift(1));
print("shift 1", sh);
valarray<double> acc(v + sh);
print("sum", acc);
valarray<double> trig(sin(v) + cos(acc));
print("trig", trig);
valarray<double> p(pow(v, 3.0));
print("3rd power", p);
valarray<double> app(v.apply(f));
print("f(v)", app);
valarray<bool> eq(v == app);
print("v == app?", eq);
double x = v.min();
double y = v.max();
double z = v.sum();
cout << "x = " << x <<
", y = " << y
<< ", z = " << z <<
endl;
} ///:~The valarray class provides a constructor that takes an array of the target type and the count of elements in the array to initialize the new valarray. The shift( ) member function shifts each valarray element one position to the left (or to the right, if its argument is negative) and fills in holes with the default value for the type (zero in this case). There is also a cshift( ) member function that does a circular shift (or “rotate”). All mathematical operators and functions are overloaded to operate on valarrays, and binary operators require valarray arguments of the same type and size. The apply( ) member function, like the transform( ) algorithm, applies a function to each element, but the result is collected into a result valarray. The relational operators return suitably-sized instances of valarray<bool> that indicate the result of element-by-element comparisons, such as with eq above. Most operations return a new result array, but a few, such as min( ), max( ), and sum( ), return a single scalar value, for obvious reasons.
The most interesting thing you can do with valarrays is reference subsets of their elements, not only for extracting information, but also for updating it. A subset of a valarray is called a slice, and certain operators use slices to do their work. The following sample program uses slices:
//: C07:Valarray2.cpp {-bor}{-dmc}
// Illustrates slices and masks.
#include "PrintValarray.h"
using namespace std;
int main() {
int data[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
};
valarray<int> v(data, 12);
valarray<int> r1(v[slice(0, 4, 3)]);
print("slice(0,4,3)", r1);
// Extract conditionally
valarray<int> r2(v[v > 6]);
print("elements > 6", r2);
// Square first column
v[slice(0, 4, 3)] *= valarray<int>(v[slice(0,
4, 3)]);
print("after squaring first column", v);
// Restore it
int idx[] = { 1, 4, 7, 10 };
valarray<int> save(idx, 4);
v[slice(0, 4, 3)] = save;
print("v restored", v);
// Extract a 2-d subset: { { 1, 3, 5 }, { 7, 9, 11 }
}
valarray<size_t> siz(2);
siz[0] = 2;
siz[1] = 3;
valarray<size_t> gap(2);
gap[0] = 6;
gap[1] = 2;
valarray<int> r3(v[gslice(0, siz, gap)]);
print("2-d slice", r3);
// Extract a subset via a boolean mask (bool
elements)
valarray<bool> mask(false, 5);
mask[1] = mask[2] = mask[4] = true;
valarray<int> r4(v[mask]);
print("v[mask]", r4);
// Extract a subset via an index mask (size_t
elements)
size_t idx2[] = { 2, 2, 3, 6 };
valarray<size_t> mask2(idx2, 4);
valarray<int> r5(v[mask2]);
print("v[mask2]", r5);
// Use an index mask in assignment
valarray<char> text("now is the
time", 15);
valarray<char> caps("NITT", 4);
valarray<size_t> idx3(4);
idx3[0] = 0;
idx3[1] = 4;
idx3[2] = 7;
idx3[3] = 11;
text[idx3] = caps;
print("capitalized", text);
} ///:~A slice object takes three arguments: the starting index, the number of elements to extract, and the “stride,” which is the gap between elements of interest. Slices can be used as indexes into an existing valarray, and a new valarray containing the extracted elements is returned. A valarray of bool, such as is returned by the expression v > 6, can be used as an index into another valarray; the elements corresponding to the true slots are extracted. As you can see, you can also use slices and masks as indexes on the left side of an assignment. A gslice object (for “generalized slice”) is like a slice, except that the counts and strides are themselves arrays, which means you can interpret a valarray as a multidimensional array. The example above extracts a 2 by 3 array from v, where the numbers start at zero and the numbers for the first dimension are found six slots apart in v, and the others two apart, which effectively extracts the matrix
1 3 5
7 9 11Here is the complete output for this program:
slice(0,4,3): 1 4 7 10
elements > 6: 7 8 9 10
after squaring v: 1 2 3 16 5 6 49 8 9 100 11 12
v restored: 1 2 3 4 5 6 7 8 9 10 11 12
2-d slice: 1 3 5 7 9 11
v[mask]: 2 3 5
v[mask2]: 3 3 4 7
capitalized: N o w I s T h e T i m eA practical example of slices is found in matrix multiplication. Consider how you would write a function to multiply two matrices of integers with arrays.
void matmult(const int a[][MAXCOLS], size_t m, size_t
n,
const int b[][MAXCOLS], size_t p, size_t
q,
int result[][MAXCOLS);This function multiplies the m-by-n matrix a by the p-by-q matrix b, where n and p are expected to be equal. As you can see, without something like valarray, you need to fix the maximum value for the second dimension of each matrix, since locations in arrays are statically determined. It is also difficult to return a result array by value, so the caller usually passes the result array as an argument.
Using valarray, you can not only pass any size matrix, but you can also easily process matrices of any type, and return the result by value. Here's how:
//: C07:MatrixMultiply.cpp
// Uses valarray to multiply matrices
#include <cassert>
#include <cstddef>
#include <cmath>
#include <iostream>
#include <iomanip>
#include <valarray>
using namespace std;
// Prints a valarray as a square matrix
template<class T>
void printMatrix(const valarray<T>& a, size_t
n) {
size_t siz = n*n;
assert(siz <= a.size());
for(size_t i = 0; i < siz; ++i) {
cout << setw(5) << a[i];
cout << ((i+1)%n ? ' ' : '\n');
}
cout << endl;
}
// Multiplies compatible matrices in valarrays
template<class T>
valarray<T>
matmult(const valarray<T>& a, size_t arows,
size_t acols,
const valarray<T>& b, size_t brows,
size_t bcols) {
assert(acols == brows);
valarray<T> result(arows * bcols);
for(size_t i = 0; i < arows; ++i)
for(size_t j = 0; j < bcols; ++j) {
// Take dot product of row a[i] and col b[j]
valarray<T> row = a[slice(acols*i, acols,
1)];
valarray<T> col = b[slice(j, brows,
bcols)];
result[i*bcols + j] = (row * col).sum();
}
return result;
}
int main() {
const int n = 3;
int adata[n*n] = {1,0,-1,2,2,-3,3,4,0};
int bdata[n*n] = {3,4,-1,1,-3,0,-1,1,2};
valarray<int> a(adata, n*n);
valarray<int> b(bdata, n*n);
valarray<int> c(matmult(a, n, n, b, n, n));
printMatrix(c, n);
} ///:~Each entry in the result matrix c is the dot product of a row in a with a column in b. By taking slices, you can extract these rows and columns as valarrays and use the global * operator and sum( ) function provided by valarray to do the work succinctly. The result valarray is computed at runtime; there's no need to worry about the static limitations of array dimensions. You do have to compute linear offsets of the position [i][j] yourself (see the formula i*bcols + j above), but the size and type freedom is worth it.
2-5-16. Summary▲
The goal of this chapter was not just to introduce the STL containers in some considerable depth. Although every detail could not be covered here, you now know enough that you can look up further information in the other resources. Our hope is that this chapter has helped you grasp the power available in the STL and shown you how much faster and more efficient your programming activities can be by understanding and using the STL.
2-5-17. Exercises▲
Solutions to selected exercises can be found in the electronic document The Thinking in C++ Volume 2 Annotated Solution Guide, available for a small fee from www.MindView.net.
- Create a set<char>, open a file (whose name is provided on the command line), and read that file in a char at a time, placing each char in the set. Print the results, and observe the organization. Are there any letters in the alphabet that are not used in that particular file?
- Create three sequences of Noisy objects, a vector, deque, and list. Sort them. Now write a function template to receive the vector and deque sequences as a parameter to sort them and record the sorting time. Write a specialized template function to do the same for list (ensure to call its member sort( ) instead of the generic algorithm). Compare the performance of the different sequence types.
- Write a program to compare the speed of sorting a list using list::sort( ) vs. using std::sort( ) (the STL algorithm version of sort( )).
- Create a generator that produces random int values between 0 and 20 inclusive, and use it to fill a multiset<int>. Count the occurrences of each value, following the example given in MultiSetWordCount.cpp.
- Change StlShape.cpp so that it uses a deque instead of a vector.
- Modify Reversible.cpp so it works with deque and list instead of vector.
- Use a stack<int> and populate it with a Fibonacci sequence. The program's command line should take the number of Fibonacci elements desired, and you should have a loop that looks at the last two elements on the stack and pushes a new one for every pass through the loop.
- Using only three stacks (source, sorted, and losers), sort a random sequence of numbers by first placing the numbers on the source stack. Assume the number on the top of the source is the largest, and push it on the sorted stack. Continue to pop the source stack comparing it with the top of the sorted stack. Whichever number is the smallest, pop it from its stack and push it onto the on the losers' stack. Once the source stack is empty, repeat the process using the losers' stack as the source stack, and use the source stack as the losers' stack. The algorithm completes when all the numbers have been placed into the winners' stack.
- Open a text file whose name is provided on the command line. Read the file a word at a time, and use a multiset<string> to create a word count for each word.
- Modify WordCount.cpp so that it uses insert( ) instead of operator[ ] to insert elements in the map.
- Create a class that has an operator< and an ostream& operator<<. The class should contain a priority number. Create a generator for your class that makes a random priority number. Fill a priority_queue using your generator, and then pull the elements out to show they are in the proper order.
- Rewrite Ring.cpp so it uses a deque instead of a list for its underlying implementation.
- Modify Ring.cpp so that the underlying implementation can be chosen using a template argument. (Let that template argument default to list.)
- Create an iterator class called BitBucket that just absorbs whatever you send to it without writing it anywhere.
- Create a kind of “hangman” game. Create a class that contains a char and a bool to indicate whether that char has been guessed yet. Randomly select a word from a file, and read it into a vector of your new type. Repeatedly ask the user for a character guess, and after each guess, display the characters in the word that have been guessed, and display underscores for the characters that haven't. Allow a way for the user to guess the whole word. Decrement a value for each guess, and if the user can get the whole word before the value goes to zero, they win.
- Open a file and read it into a single string. Turn the string into a stringstream. Read tokens from the stringstream into a list<string> using a TokenIterator.
- Compare the performance of stack based on whether it is implemented with vector, deque, or list.
- Create a template that implements a singly-linked list called SList. Provide a default constructor and begin( ) and end( ) functions (via an appropriate nested iterator), insert( ), erase( ) and a destructor.
- Generate a sequence of random integers, storing them into an array of int. Initialize a valarray<int> with its contents. Compute the sum, minimum value, maximum value, average, and median of the integers using valarray operations.
- Create a valarray<int> with 12 random values. Create another valarray<int> with 20 random values. You will interpret the first valarray as a 3 x 4 matrix of ints and the second as a 4 x 5 matrix of ints, and multiply them by the rules of matrix multiplication. Store the result in a valarray<int> of size 15, representing the 3 x 5 result matrix. Use slices to multiply the rows of the first matrix time the columns of the second. Print the result in rectangular matrix form.