Thinking in C++ - Volume 2
Thinking in C++ - Volume 2
Date de publication : 25/01/2007 , Date de mise à jour : 25/01/2007
2.3. Templates in Depth
2.3.1. Template parameters
2.3.1.1. Non–type template parameters
2.3.1.2. Default template arguments
2.3.1.3. Template template parameters
2.3.1.4. The typename keyword
2.3.1.5. Using the template keyword as a hint
2.3.1.6. Member Templates
2.3.2. Function template issues
2.3.2.1. Type deduction of function template arguments
2.3.2.2. Function template overloading
2.3.2.3. Taking the address of a generated function template
2.3.2.4. Applying a function to an STL sequence
2.3.2.5. Partial ordering of function templates
2.3.3. Template specialization
2.3.3.1. Explicit specialization
2.3.3.2. Partial Specialization
2.3.3.3. A practical example
2.3.3.4. Preventing template code bloat
2.3.4. Name lookup issues
2.3.4.1. Names in templates
2.3.4.2. Templates and friends
2.3.5. Template programming idioms
2.3.5.1. Traits
2.3.5.2. Policies
2.3.5.3. The curiously recurring template pattern
2.3.6. Template metaprogramming
2.3.6.1. Compile–time programming
2.3.6.2. Expression templates
2.3.7. Template compilation models
2.3.7.1. The inclusion model
2.3.7.2. Explicit instantiation
2.3.7.3. The separation model
2.3.8. Summary
2.3.9. Exercises
2.3. Templates in Depth
The C++ template facility goes far
beyond simple “containers of T.” Although the original motivation was to
enable type–safe, generic containers, in modern C++, templates are also used to
generate custom code and to optimize program execution through compile–time
programming constructs.
In this chapter we offer a practical look at the power (and
pitfalls) of programming with templates in modern C++. For a more complete
analysis of template-related language issues and pitfalls, we recommend the
superb book by Daveed Vandevoorde and Nico Josuttis.(51)
2.3.1. Template parameters
As illustrated in Volume 1, templates come in two flavors:
function templates and class templates. Both are wholly characterized by their
parameters. Each template parameter can represent one of the following:
1. Types
(either built-in or user-defined).
2. Compile-time
constant values (for example, integers, and pointers and references to static
entities; often referred to as non-type parameters).
3. Other
templates.
The examples in Volume 1 all fall into the first category
and are the most common. The canonical example for simple container-like
templates nowadays seems to be a Stack class. Being a container, a Stack
object is not concerned with the type of object it stores; the logic of holding
objects is independent of the type of objects being held. For this reason you
can use a type parameter to represent the contained type:
|
The actual type to be used for a particular Stack
instance is determined by the argument for the parameter T:
|
The compiler then provides an int-version of Stack
by substituting int for T and generating the corresponding code.
The name of the class instance generated from the template in this case is Stack<int>.
2.3.1.1. Non–type template parameters
A non-type template parameter must be an integral value that
is known at compile time. You can make a fixed-size Stack, for instance,
by specifying a non-type parameter to be used as the dimension for the
underlying array, as follows.
|
You must provide a compile-time constant value for the
parameter N when you request an instance of this template, such as
|
Because the value of N is known at compile time, the
underlying array (data) can be placed on the runtime stack instead of on the free store. This can improve runtime performance by avoiding the overhead
associated with dynamic memory allocation. Following the pattern mentioned
earlier, the name of the class above is Stack<int, 100>. This
means that each distinct value of N results in a unique class type. For
example, Stack<int, 99> is a distinct class from Stack<int, 100>.
The bitset class template, discussed in detail in Chapter
7, is the only class in the Standard C++ library that uses a non-type template
parameter (which specifies the number of bits the bitset object can hold).
The following random number generator example uses a bitset to track
numbers so all the numbers in its range are returned in random order without
repetition before starting over. This example also overloads operator( ) to produce a familiar function-call syntax.
|
The numbers generated by Urand are unique because the
bitset used tracks all the possible numbers in the random space
(the upper bound is set with the template argument) and records each used number
by setting the corresponding position bit. When the numbers are all used up, the
bitset is cleared to start over. Here's a simple driver that illustrates
how to use a Urand object:
|
As we explain later in this chapter, non-type template
arguments are also important in the optimization of numeric computations.
2.3.1.2. Default template arguments
You can provide default arguments for template parameters in
class templates, but not function templates. As with default function
arguments, they should only be defined once, the first time a template
declaration or definition is seen by the compiler. Once you introduce a default
argument, all the subsequent template parameters must also have defaults. To
make the fixed-size Stack template shown earlier a little friendlier,
for example, you can add a default argument like this:
|
Now, if you omit the second template argument when declaring
a Stack object, the value for N will default to 100.
You can choose to provide defaults for all arguments, but
you must use an empty set of brackets when declaring an instance so that the
compiler knows that a class template is involved:
|
Default arguments are used heavily in the Standard C++
library. The vector class template, for instance, is declared as
follows:
|
Note the space between the last two right angle bracket
characters. This prevents the compiler from interpreting those two characters (>>)
as the right-shift operator.
This declaration reveals that vector takes two
arguments: the type of the contained objects it holds, and a type that
represents the allocator used by the vector. Whenever you omit the
second argument, the standard allocator template is used, parameterized
by the first template parameter. This declaration also shows that you can use
template parameters in subsequent template parameters, as T is used
here.
Although you cannot use default template arguments in
function templates, you can use template parameters as default arguments to
normal functions. The following function template adds the elements in a
sequence:
|
The third argument to sum( ) is the initial
value for the accumulation of the elements. Since we omitted it, this argument
defaults to T( ), which in the case of int and other
built-in types invokes a pseudo-constructor that performs zero-initialization.
2.3.1.3. Template template parameters
The third type of parameter a template can accept is another
class template. If you are going to use a template type parameter itself as a
template in your code, the compiler needs to know that the parameter is a
template in the first place. The following example illustrates a template
template parameter:
|
The Array class template is a trivial sequence
container. The Container template takes two parameters: the type that it
holds, and a sequence data structure to do the holding. The following line in
the implementation of the Container class requires that we inform the
compiler that Seq is a template:
|
If we hadn't declared Seq to be a template template
parameter, the compiler would complain here that Seq is not a template,
since we're using it as such. In main( ) a Container is
instantiated to use an Array to hold integers, so Seq stands for Array
in this example.
Note that it is not necessary in this case to name the
parameter for Seq inside Container's declaration. The line in
question is:
|
Although we could have written
|
the parameter U is not needed anywhere. All that
matters is that Seq is a class template that takes a single type
parameter. This is analogous to omitting the names of function parameters when
they're not needed, such as when you overload the post-increment operator:
|
The int here is merely a placeholder and so needs no
name.
The following program uses a fixed-size array, which has an
extra template parameter representing the array length:
|
Once again, parameter names are not needed in the
declaration of Seq inside Container's declaration, but we need
two parameters to declare the data member seq, hence the appearance of
the non-type parameter N at the top level.
Combining default arguments with template template parameters
is slightly more problematic. When the compiler looks at the inner parameters
of a template template parameter, default arguments are not considered, so you
have to repeat the defaults in order to get an exact match. The following
example uses a default argument for the fixed-size Array template and
shows how to accommodate this quirk in the language:
|
The default dimension of 10 is required in the line:
|
Both the definition of seq in Container and container
in main( ) use the default. The only way to use something other
than the default value was shown in TempTemp2.cpp. This is the only
exception to the rule stated earlier that default arguments should appear only
once in a compilation unit.
Since the standard sequence containers (vector, list,
and deque, discussed in depth in Chapter 7) have a default allocator
argument, the technique shown above is helpful should you ever want to pass one
of these sequences as a template parameter. The following program passes a vector
and then a list to two instances of Container:
|
Here we name the first parameter of the inner template Seq
(with the name U) because the allocators in the standard sequences must
themselves be parameterized with the same type as the contained objects in the
sequence. Also, since the default allocator parameter is known, we can
omit it in the subsequent references to Seq<T>, as we did in the
previous program. To fully explain this example, however, we have to discuss
the semantics of the typename keyword.
2.3.1.4. The typename keyword
Consider the following:
|
The template definition assumes that the class T that
you hand it must have a nested identifier of some kind called id. Yet id
could also be a static data member of T, in which case you can perform
operations on id directly, but you can't “create an object” of “the type
id.” In this example, the identifier id is being treated as if it
were a nested type inside T. In the case of class Y, id is
in fact a nested type, but (without the typename keyword) the compiler
can't know that when it's compiling X.
If the compiler has the option of treating an identifier as
a type or as something other than a type when it sees an identifier in a
template, it will assume that the identifier refers to something other than a
type. That is, it will assume that the identifier refers to an object
(including variables of primitive types), an enumeration, or something similar.
However, it will not—cannot—just assume that it is a type.
Because the default behavior of the compiler is to assume that
a name that fits the above two points is not a type, you must use typename
for nested names (except in constructor initializer lists, where it is neither
needed nor allowed). In the above example, when the compiler sees typename
T::id, it knows (because of the typename keyword) that id
refers to a nested type and thus it can create an object of that type.
The short version of the rule is: if a type referred to
inside template code is qualified by a template type parameter, you must use
the typename keyword as a prefix, unless it appears in a base class
specification or initializer list in the same scope (in which case you must
not).
The above explains the use of the typename keyword in
the program TempTemp4.cpp. Without it, the compiler would assume that
the expression Seq<T>::iterator is not a type, but we were using
it to define the return type of the begin( ) and end( )
member functions.
The following example, which defines a function template
that can print any Standard C++ sequence, shows a similar use of typename:
|
Once again, without the typename keyword the compiler
will interpret iterator as a static data member of Seq<T>,
which is a syntax error, since a type is required.
Typedefing a typename
It's important not to assume that the typename
keyword creates a new type name. It doesn't. Its purpose is to inform the
compiler that the qualified identifier is to be interpreted as a type. A line that
reads:
|
causes a variable named It to be declared of type Seq<T>::iterator.
If you mean to create a new type name, you should use typedef, as usual,
as in:
|
Using typename instead of class
Another role of the typename keyword is to provide
you the option of using typename instead of class in the template
argument list of a template definition:
|
To some, this produces clearer code.
2.3.1.5. Using the template keyword as a hint
Just as the typename keyword helps the compiler when
a type identifier is not expected, there is also a potential difficulty with
tokens that are not identifiers, such as the < and >
characters. Sometimes these represent the less-than or greater-than symbols,
and sometimes they delimit template parameter lists. As an example, we'll once
more use the bitset class:
|
The bitset class supports conversion to string object
via its to_string member function. To support multiple string classes, to_string
is itself a template, following the pattern established by the basic_string
template discussed in Chapter 3. The declaration of to_string inside of bitset looks like this:
|
Our bitsetToString( ) function template above
requests different types of string representations of a bitset. To get a
wide string, for instance, you change the call to the following:
|
Note that basic_string uses default template arguments, so we don't need to repeat the char_traits and allocator arguments in the return value. Unfortunately, bitset::to_string does not use default
arguments. Using bitsetToString<char>( bs) is more convenient
than typing a fully-qualified call to bs.template to_string<char,
char_traits, allocator<char> >( ) every time.
The return statement in bitsetToString( )
contains the template keyword in an odd place—right after the dot
operator applied to the bitset object bs. This is because when
the template is parsed, the < character after the to_string
token would be interpreted as a less-than operation instead of the beginning of
a template argument list. The template keyword used in this context tells
the compiler that what follows is the name of a template, causing the <
character to be interpreted correctly. The same reasoning applies to the ->
and ::operators when applied to templates. As with the typename
keyword, this template disambiguation technique can only be used within
template code.(52)
2.3.1.6. Member Templates
The bitset::to_string( ) function template is an
example of a member template: a template declared within another class
or class template. This allows many combinations of independent template
arguments to be combined. A useful example is found in the complex class
template in the Standard C++ library. The complex template has a type
parameter meant to represent an underlying floating-point type to hold the real
and imaginary parts of a complex number. The following code snippet from the
standard library shows a member-template constructor in the complex
class template:
|
The standard complex template comes ready-made with
specializations that use float, double, and long double
for the parameter T. The member-template constructor above creates a new
complex number that uses a different floating-point type as its base type, as
seen in the code below:
|
In the declaration of w, the complex template
parameter T is double and X is float. Member
templates make this kind of flexible conversion easy.
Defining a template within a template is a nesting
operation, so the prefixes that introduce the templates must reflect this
nesting if you define the member template outside the outer class definition.
For example, if you implement the complex class template, and if you
define the member-template constructor outside the complex template
class definition, you do it like this:
|
Another use of member function templates in the standard
library is in the initialization of containers. Suppose we have a vector
of ints and we want to initialize a new vector of doubles
with it, like this:
|
As long as the elements in v1 are
assignment-compatible with the elements in v2 (as double and int
are here), all is well. The vector class template has the following
member template constructor:
|
This constructor is used twice in the vector
declarations above. When v1 is initialized from the array of ints,
the type InputIterator is int*. When v2 is initialized
from v1, an instance of the member template constructor is used with InputIterator
representing vector<int>::iterator.
Member templates can also be classes. (They don't need to be
functions.) The following example shows a member class template inside an outer
class template:
|
The typeid operator, covered in Chapter 8, takes a
single argument and returns a type_info object whose name( )
function yields a string representing the argument type. For example, typeid(int).name( )
might return the string “int.” (The actual string is
platform-dependent.) The typeid operator can also take an expression and
return a type_info object representing the type of that expression. For
example, with int i, typeid(i).name( ) returns something
like “int,” and typeid(&i).name( ) returns something
like “int *.”
The output of the program above should be something like
this:
|
The declaration of the variable inner in the main
program instantiates both Inner<bool> and Outer<int>.
Member template functions cannot be declared virtual. Current compiler technology expects to be able to determine the size of a
class's virtual function table when the class is parsed. Allowing virtual
member template functions would require knowing all calls to such member
functions everywhere in the program ahead of time. This is not feasible,
especially for multi-file projects.
2.3.2. Function template issues
Just as a class template describes a family of classes, a
function template describes a family of functions. The syntax for creating
either type of template is virtually identical, but they differ somewhat in how
they are used. You must always use angle brackets when instantiating class
templates and you must supply all non-default template arguments. However, with
function templates you can often omit the template arguments, and default
template arguments are not even allowed. Consider a typical
implementation of the min( ) function template declared in the <algorithm>
header, which looks something like this:
|
You could invoke this template by providing the type of the
arguments in angle brackets, just like you do with class templates, as in:
|
This syntax tells the compiler that a specialization of the min( )
template is needed with int used in place of the parameter T,
whereupon the compiler generates the corresponding code. Following the pattern
of naming the classes generated from class templates, you can think of the name
of the instantiated function as min<int>( ).
2.3.2.1. Type deduction of function template arguments
You can always use such explicit function template specification as in the example above, but it is often convenient to leave off the template
arguments and let the compiler deduce them from the function arguments, like
this:
|
If both i and j are ints, the compiler
knows that you need min<int>( ), which it then instantiates
automatically. The types must be identical because the template was originally
specified with only one template type argument used for both function
parameters. No standard conversions are applied for function arguments whose
type is specified by a template parameter. For example, if you wanted to find
the minimum of an int and a double, the following attempt at a
call to min( ) would fail:
|
Since x and j are distinct types, no single
parameter matches the template parameter T in the definition of min( ),
so the call does not match the template declaration. You can work around this
difficulty by casting one argument to the other's type or by reverting to the
fully-specified call syntax, as in:
|
This tells the compiler to generate the double
version of min( ), after which j can be promoted to a double
by normal standard conversion rules (because the function min<double>(const
double&, const double&) would then exist).
You might be tempted to require two parameters for min( ),
allowing the types of the arguments to be independent, like this:
|
This is often a good strategy, but here it is problematic
because min( ) must return a value, and there is no satisfactory
way to determine which type it should be (T or U?).
If the return type of a function template is an independent
template parameter, you must always specify its type explicitly when you call
it, since there is no argument from which to deduce it. Such is the case with
the fromString template below.
|
These function templates provide conversions to and from std::string
for any types that provide a stream inserter or extractor, respectively. Here's
a test program that includes the use of the standard library complex
number type:
|
The output is what you'd expect:
|
Notice that in each of the instantiations of fromString( ),
the template parameter is specified in the call. If you have a function
template with template parameters for the parameter types as well as the return
types, it is important to declare the return type parameter first, otherwise
you won't be able to omit the type parameters for the function parameters. As
an illustration, consider the following well-known function template:(53)
|
If you interchange R and P in the template
parameter list near the top of the file, it will be impossible to compile this
program because the return type will remain unspecified (the first template
parameter would be the function's parameter type). The last line (which is
commented out) is illegal because there is no standard conversion from int
to char*. implicit_cast is for revealing conversions in your code
that are allowed naturally.
With a little care you can even deduce array dimensions. This
example has an array-initialization function template (init2) that performs
such a deduction:
|
Array dimensions are not passed as part of a function
parameter's type unless that parameter is passed by pointer or reference. The
function template init2 declares a to be a reference to a
two-dimensional array, so its dimensions R and C are deduced by
the template facility, making init2 a handy way to initialize a
two-dimensional array of any size. The template init1 does not pass the
array by reference, so the sizes must be explicitly specified, although the
type parameter can still be deduced.
2.3.2.2. Function template overloading
As with ordinary functions, you can overload function
templates that have the same name. When the compiler processes a function call
in a program, it has to decide which template or ordinary function is the
“best” fit for the call. Along with the min( ) function template
introduced earlier, let's add some ordinary functions to the mix:
|
In addition to the function template, this program defines
two non-template functions: a C-style string version of min( ) and
a double version. If the template doesn't exist, the call in line 1
above invokes the double version of min( ) because of the
standard conversion from int to double. The template can generate
an int version which is considered a better match, so that's what
happens. The call in line 2 is an exact match for the double version,
and the call in line 3 also invokes the same function, implicitly converting 1
to 1.0. In line 4 the const char* version of min( ) is
called directly. In line 5 we force the compiler to use the template facility
by appending empty angle brackets to the function name, whereupon it generates
a const char* version from the template and uses it (which is verified
by the wrong answer—it's just comparing addresses!(54)).
If you're wondering why we have using declarations in lieu of the using
namespace std directive, it's because some compilers include headers behind
the scenes that bring in std::min( ), which would conflict with our
declarations of the name min( ).
As stated above, you can overload templates of the same
name, as long as they can be distinguished by the compiler. You could, for
example, declare a min( ) function template that processes three
arguments:
|
Versions of this template will be generated only for calls
to min( ) that have three arguments of the same type.
2.3.2.3. Taking the address of a generated function template
In some situations you need to take the address of a
function. For example, you may have a function that takes an argument of a
pointer to another function. It's possible that this other function might be
generated from a template function, so you need some way to take that kind of
address:(55)
|
This example demonstrates a number of issues. First, even
though you're using templates, the signatures must match. The function h( )
takes a pointer to a function that takes an int* and returns void,
and that's what the template f( ) produces. Second, the function
that wants the function pointer as an argument can itself be a template, as in
the case of the template g( ).
In main( ) you can see that type deduction works
here, too. The first call to h( ) explicitly gives the template
argument for f( ), but since h( ) says that it will
only take the address of a function that takes an int*, that part can be
deduced by the compiler. With g( ) the situation is even more
interesting because two templates are involved. The compiler cannot deduce the
type with nothing to go on, but if either f( ) or g( )
is given int, the rest can be deduced.
An obscure issue arises when trying to pass the functions tolower or toupper, declared in <cctype>, as parameters. It is possible to use these, for example, with the transform algorithm (which is covered in detail in the next chapter) to convert a string to lower or upper case. You must be careful because
there are multiple declarations for these functions. A naive approach would be
something like this:
|
The transform algorithm applies its fourth parameter
(tolower( ) in this case) to each character in the string s
and places the result in s itself, thus overwriting each character in s
with its lower-case equivalent. As it is written, this statement may or may not
work! It fails in the following context:
|
Even if your compiler lets you get away with this, it is
illegal. The reason is that the <iostream> header also makes
available a two-argument version of tolower( ) and toupper( ):
|
These function templates take a second argument of type locale.
The compiler has no way of knowing whether it should use the one-argument
version of tolower( ) defined in <cctype> or the one
mentioned above. You can solve this problem (almost!) with a cast in the call
to transform, as follows:
|
(Recall that tolower( ) and toupper( ) work
with int instead of char.) The cast above makes clear that the
single-argument version of tolower( ) is desired. This works with
some compilers, but it is not required to. The reason, albeit obscure, is that
a library implementation is allowed to give “C linkage” (meaning that the
function name does not contain all the auxiliary information(56) that
normal C++ functions do) to functions inherited from the C language. If this is
the case, the cast fails because transform is a C++ function template
and expects its fourth argument to have C++ linkage—and a cast is not allowed
to change the linkage. What a predicament!
The solution is to place tolower( ) calls in an
unambiguous context. For example, you could write a function named strTolower( )
and place it in its own file without including <iostream>, like
this:
|
The header <iostream> is not involved here, and
the compilers we use do not introduce the two-argument version of tolower( )
in this context,(57) so
there's no problem. You can then use this function normally:
|
Another solution is to write a wrapper function template
that calls the correct version of tolower( ) explicitly:
|
This version has the advantage that it can process both wide
and narrow strings since the underlying character type is a template parameter.
The C++ Standards Committee is working on modifying the language so that the
first example (without the cast) will work, and some day these workarounds can
be ignored.(58)
2.3.2.4. Applying a function to an STL sequence
Suppose you want to take an STL sequence container (which
you'll learn more about in subsequent chapters; for now we can just use the
familiar vector) and apply a member function to all the objects it contains.
Because a vector can contain any type of object, you need a function
that works with any type of vector:
|
The apply( ) function template above takes a
reference to the container class and a pointer-to-member for a member function
of the objects contained in the class. It uses an iterator to move through the
sequence and apply the function to every object. We have overloaded on the const-ness
of the function so you can use it with both const and non-const
functions.
Notice that there are no STL header files (or any header
files, for that matter) included in applySequence.h, so it is not
limited to use with an STL container. However, it does make assumptions
(primarily, the name and behavior of the iterator) that apply to STL
sequences, and it also assumes that the elements of the container be of pointer
type.
You can see there is more than one version of apply( ),
further illustrating overloading of function templates. Although these
templates allow any type of return value (which is ignored, but the type
information is required to match the pointer-to-member), each version takes a
different number of arguments, and because it's a template, those arguments can
be of any type. The only limitation here is that there's no “super template” to
create templates for you; you must decide how many arguments will ever be
required and make the appropriate definitions.
To test the various overloaded versions of apply( ),
the class Gromit(59) is
created containing functions with different numbers of arguments, and both const
and non-const member functions:
|
Now you can use the apply( ) template functions to
apply the Gromit member functions to a vector<Gromit*>,
like this:
|
The purge( ) function is a small utility that
calls delete on every element of sequence. You'll find it defined in
Chapter 7, and used various places in this book.
Although the definition of apply( ) is somewhat
complex and not something you'd ever expect a novice to understand, its use is
remarkably clean and simple, and a novice could use it knowing only what
it is intended to accomplish, not how. This is the type of division you
should strive for in all your program components. The tough details are all
isolated on the designer's side of the wall. Users are concerned only with
accomplishing their goals and don't see, know about, or depend on details of
the underlying implementation. We'll explore even more flexible ways to apply
functions to sequences in the next chapter.
2.3.2.5. Partial ordering of function templates
We mentioned earlier that an ordinary function overload of min( ) is preferable to using the template. If a function already exists
to match a function call, why generate another? In the absence of ordinary
functions, however, it is possible that overloaded function templates can lead
to ambiguities. To minimize the chances of this, an ordering is defined for
function templates, which chooses the most specialized template, if such
exists. A function template is considered more specialized than another if
every possible list of arguments that matches it also matches the other, but
not the other way around. Consider the following function template
declarations, taken from an example in the C++ Standard document:
|
The first template can be matched with any type. The second
template is more specialized than the first because only pointer types match
it. In other words, you can look upon the set of possible calls that match the
second template as a subset of the first. A similar relationship exists between
the second and third template declarations above: the third can only be called
for pointers to const, but the second accommodates any pointer type. The
following program illustrates these rules:
|
The call f(&i) certainly matches the first
template, but since the second is more specialized, it is called. The third
can't be called here since the pointer is not a pointer to const. The
call f(&j) matches all three templates (for example, T would
be const int in the second template), but again, the third template is
more specialized, so it is used instead.
If there is no “most specialized” template among a set of
overloaded function templates, an ambiguity remains, and the compiler will
report an error. That is why this feature is called a “partial ordering”—it may
not be able to resolve all possibilities. Similar rules exist for class
templates (see the section “Partial specialization” below).
2.3.3. Template specialization
The term specialization has a specific,
template-related meaning in C++. A template definition is, by its very nature,
a generalization, because it describes a family of functions or classes
in general terms. When template arguments are supplied, the result is a
specialization of the template because it determines a unique instance out of
the many possible instances of the family of functions or classes. The min( )
function template seen at the beginning of this chapter is a generalization of
a minimum-finding function because the type of its parameters is not specified.
When you supply the type for the template parameter, whether explicitly or
implicitly via argument deduction, the resultant code generated by the compiler
(for example, min<int>( )) is a specialization of the
template. The code generated is also considered an instantiation of the template, as are all code bodies generated by the template facility.
2.3.3.1. Explicit specialization
You can also provide the code yourself for a given template
specialization, should the need arise. Providing your own template
specializations is often needed with class templates, but we will begin with
the min( ) function template to introduce the syntax.
Recall that in MinTest.cpp earlier in this chapter we
introduced the following ordinary function:
|
This was so that a call to min( ) would compare
strings and not addresses. Although it would provide no advantage here, we
could instead define a const char* specialization for min( ),
as in the following program:
|
The “template<>” prefix tells the compiler that
what follows is a specialization of a template. The type for the specialization
must appear in angle brackets immediately following the function name, as it normally
would in an explicitly specified call. Note that we carefully substitute
const char* for T in the explicit specialization. Whenever the
original template specifies const T, that const modifies the whole
type T. It is the pointer to a const char* that is const. So
we must write const char* const in place of const T in the specialization.
When the compiler sees a call to min( ) with const char*
arguments in the program, it will instantiate our const char* version of
min( ) so it can be called. The two calls to min( ) in
this program call the same specialization of min( ).
Explicit specializations tend to be more useful for class
templates than for function templates. When you provide a full specialization
for a class template, though, you may need to implement all the member
functions. This is because you are providing a separate class, and client code
may expect the complete interface to be implemented.
The standard library has an explicit specialization for vector
when it holds objects of type bool. The purpose for vector<bool>
is to allow library implementations to save space by packing bits into
integers.(60)
As you saw earlier in this chapter, the declaration for the
primary vector class template is:
|
To specialize for objects of type bool, you could
declare an explicit specialization as follows:
|
Again, this is quickly recognized as a full, explicit
specialization because of the template<> prefix and because all
the primary template's parameters are satisfied by the argument list appended
to the class name.
It turns out that vector<bool> is a little more
flexible than we have described, as seen in the next section.
2.3.3.2. Partial Specialization
Class templates can also be partially specialized, meaning
that at least one of the template parameters is left “open” in some way in the
specialization. vector<bool> specifies the object type (bool),
but leaves the allocator type unspecified. Here is the actual declaration of vector<bool>:
|
You can recognize a partial specialization because non-empty
parameter lists appear in angle brackets both after the template keyword (the
unspecified parameters) and after the class (the specified arguments). Because
of the way vector<bool> is defined, a user can provide a custom
allocator type, even though the contained type of bool is fixed. In
other words, specialization, and partial specialization in particular,
constitute a sort of “overloading” for class templates.
Partial ordering of class templates
The rules that determine which template is selected for instantiation are similar to the partial ordering for function templates—the “most
specialized” template is selected. The string in each f( ) member
function in the illustration below explains the role of each template
definition:
|
As you can see, you can partially specify template
parameters according to whether they are pointer types, or whether they are
equal. When the T* specialization is used, such as is the case in line
5, T itself is not the top-level pointer type that was passed—it is the
type that the pointer refers to (float, in this case). The T*
specification is a pattern to allow matching against pointer types. If you use int**
as the first template argument, T becomes int*. Line 8 is
ambiguous because having the first parameter as an int versus having the
two parameters equal are independent issues—one is not more specialized than
the other. Similar logic applies to lines 9 through 12.
2.3.3.3. A practical example
You can easily derive from a class template, and you can
create a new template that instantiates and inherits from an existing template.
If the vector template does most everything you want, for example, but in
a certain application you'd also like a version that can sort itself, you can
easily reuse the vector code. The following example derives from vector<T>
and adds sorting. Note that deriving from vector, which doesn't have a
virtual destructor, would be dangerous if we needed to perform cleanup in our
destructor.
|
The Sortable template imposes a restriction on all
but one of the classes for which it is instantiated: they must contain a >
operator. It works correctly only with non-pointer objects (including objects
of built-in types). The full specialization compares the elements using strcmp( )
to sort vectors of char* according to the null-terminated strings
to which they refer. The use of “this->” above is mandatory(61) and is
explained in the section entitled “Name lookup issues” later in this chapter.(62)
Here's a driver for Sortable.h that uses the randomizer
introduced earlier in the chapter:
|
Each of the template instantiations above uses a different
version of the template. Sortable<int> uses the primary template. Sortable<string*>
uses the partial specialization for pointers. Last, Sortable<char*>
uses the full specialization for char*. Without this full
specialization, you could be fooled into thinking that things were working
correctly because the words array would still sort out to “a big dog is
running” since the partial specialization would end up comparing the first
character of each array. However, words2 would not sort correctly.
2.3.3.4. Preventing template code bloat
Whenever a class template is instantiated, the code from the
class definition for the particular specialization is generated, along with all
the member functions that are called in the program. Only the member functions
that are called are generated. This is good, as you can see in the following
program:
|
Here, even though the template Z purports to use both
f( ) and g( ) member functions of T, the fact
that the program compiles shows you that it only generates Z<X>::a( )
when it is explicitly called for zx. (If Z<X>::b( )
were also generated at the same time, a compile-time error message would be
generated because it would attempt to call X::g( ), which doesn't
exist.) Similarly, the call to zy.b( ) doesn't generate Z<Y>::a( ).
As a result, the Z template can be used with X and Y,
whereas if all the member functions were generated when the class was first instantiated
the use of many templates would become significantly limited.
Suppose you have a templatized Stack container and
you use specializations for int, int*, and char*. Three
versions of Stack code will be generated and linked as part of your
program. One of the reasons for using a template in the first place is so you don't
need to replicate code by hand; but code still gets replicated—it's just the
compiler that does it instead of you. You can factor the bulk of the
implementation for storing pointer types into a single class by using a combination
of full and partial specialization. The key is to fully specialize for void*
and then derive all other pointer types from the void* implementation so
the common code can be shared. The program below illustrates this technique:
|
This simple stack expands as it fills its capacity. The void*
specialization stands out as a full specialization by virtue of the template<>
prefix (that is, the template parameter list is empty). As mentioned earlier,
it is necessary to implement all member functions in a class template
specialization. The savings occurs with all other pointer types. The partial
specialization for other pointer types derives from Stack<void*>
privately, since we are merely using Stack<void*> for
implementation purposes, and do not wish to expose any of its interface
directly to the user. The member functions for each pointer instantiation are
small forwarding functions to the corresponding functions in Stack<void*>.
Hence, whenever a pointer type other than void* is instantiated, it is a
fraction of the size it would have been had the primary template alone been
used.(63) Here is a driver
program:
|
For convenience we include two emptyStack function templates.
Since function templates don't support partial specialization, we provide
overloaded templates. The second version of emptyStack is more
specialized than the first, so it is chosen whenever pointer types are used. Three
class templates are instantiated in this program: Stack<int>, Stack<void*>,
and Stack<int*>. Stack<void*> is implicitly
instantiated because Stack<int*> derives from it. A program using
instantiations for many pointer types can produce substantial savings in code
size over just using a single Stack template.
2.3.4. Name lookup issues
When the compiler encounters an identifier it must determine
the type and scope (and in the case of variables, the lifetime) of the entity
the identifier represents. Templates add complexity to the situation. Because the
compiler doesn't know everything about a template when it first sees the
definition, it can't tell whether the template is being used properly until it
sees the template instantiation. This predicament leads to a two-phase process
for template compilation.
2.3.4.1. Names in templates
In the first phase, the compiler parses the template
definition looking for obvious syntax errors and resolving all the names it
can. It can resolve names that do not depend on template parameters using
normal name lookup, and if necessary through argument-dependent lookup (discussed
below). The names it can't resolve are the so-called dependent names, which depend on template parameters in some way. These can't be resolved
until the template is instantiated with its actual arguments. So instantiation is
the second phase of template compilation. Here, the compiler determines whether to use an explicit specialization of the template instead of the primary
template.
Before you see an example, you must understand two more
terms. A qualified name is a name with a class-name prefix, a name with
an object name and a dot operator, or a name with a pointer to an object and an
arrow operator. Examples of qualified names are:
|
We use qualified names many times in this book, and most
recently in connection with the typename keyword. These are called
qualified names because the target names (like f above) are explicitly
associated with a class or namespace, which tells the compiler where to look
for the declarations of those names.
The other term is argument-dependent lookup(64) (ADL), a mechanism
originally designed to simplify non-member function calls (including operators)
declared in namespaces. Consider the following:
|
Note that, following the typical practice in header files,
there is no using namespace std directive. Without such a directive, you
must use the “std::”qualifier on the items that are in the std
namespace. We have, however, not qualified everything from std that we
are using. Can you see what is unqualified?
We have not specified which operator functions to use. We
want the following to happen, but we don't want to have to type it!
|
To make the original output statement work as desired, ADL
specifies that when an unqualified function call appears and its declaration is
not in (normal) scope, the namespaces of each of its arguments are searched for
a matching function declaration. In the original statement, the first function
call is:
|
Since there is no such function in scope in our original
excerpt, the compiler notes that this function's first argument (std::cout)
is in the namespace std; so it adds that namespace to the list of scopes
to search for a unique function that best matches the signature operator<<(std::ostream&,
std::string). It finds this function declared in the std namespace
via the <string> header.
Namespaces would be very inconvenient without ADL. Note that
ADL generally brings in all declarations of the name in question from
all eligible namespaces—if there is no single best match, an ambiguity will
result.
To turn off ADL, you can enclose the function name in
parentheses:
|
Now consider the following program:(65)
|
The only compiler we have that produces correct behavior
without modification is the Edison Design Group front end,(66) although
some compilers, such as Metrowerks, have an option to enable the correct lookup
behavior. The output should be:
|
because f is a non-dependent name that can be
resolved early by looking in the context where the template is defined, when
only f(double) is in scope. Unfortunately, there is a lot of existing code
in the industry that depends on the non-standard behavior of binding the call
to f(1) inside g( ) to the latter f(int), so compiler
writers have been reluctant to make the change.
Here is a more detailed example:(67)
|
The output from this program should be:
|
Looking at the declarations inside of X::f( ):
- E, the return type of X::f( ), is not a dependent name, so it is looked up when the template is parsed, and the typedef naming E as a double is found. This may seem strange, since with non-template classes the declaration of E in the base class would be found first, but those are the rules. (The base class, Y, is a dependent base class, so it can't be searched at template definition time).
- The call to g( ) is also non-dependent, since there is no mention of T. If g had parameters that were of class type of defined in another namespace, ADL would take over, since there is no g with parameters in scope. As it is, this call matches the global declaration of g( ).
- The call this->h( ) is a qualified name, and the object that qualifies it (this) refers to the current object, which is of type X, which in turn depends on the name Y<T> by inheritance. There is no function h( ) inside of X, so the lookup will search the scope of X's base class, Y<T>. Since this is a dependent name, it is looked up at instantiation time, when Y<T> are reliably known (including any potential specializations that might have been written after the definition of X), so it calls Y<int>::h( ).
- The declarations of t1 and t2 are dependent.
- The call to operator<<(cout, t1) is dependent, since t1 is of type T. This is looked up later when T is int, and the inserter for int is found in std.
- The unqualified call to swap( ) is dependent because its arguments are of type T. This ultimately causes a global swap(int&, int&) to be instantiated.
- The qualified call to std::swap( ) is not dependent, because std is a fixed namespace. The compiler knows to look in std for the proper declaration. (The qualifier on the left of the “::” must mention a template parameter for a qualified name to be considered dependent.) The std::swap( ) function template later generates std::swap(int&, int&), at instantiation time. No more dependent names remain in X<T>::f( ).
To clarify and summarize: name lookup is done at the point
of instantiation if the name is dependent, except that for unqualified
dependent names the normal name lookup is also attempted early, at the point of
definition. All non-dependent names in templates are looked up early, at the
time the template definition is parsed. (If necessary, another lookup occurs at
instantiation time, when the type of the actual argument is known.)
If you have studied this example to the point that you
understand it, prepare yourself for yet another surprise in the following
section on friend declarations.
2.3.4.2. Templates and friends
A friend function declaration inside a class allows a
non-member function to access non-public members of that class. If the friend
function name is qualified, it will be found in the namespace or class that
qualifies it. If it is unqualified, however, the compiler must make an
assumption about where the definition of the friend function will be, since all
identifiers must have a unique scope. The expectation is that the function will
be defined in the nearest enclosing namespace (non-class) scope that contains
the class granting friendship. Often this is just the global scope. The
following non-template example clarifies this issue:
|
The declaration of f( ) inside the Friendly
class is unqualified, so the compiler will expect to be able to eventually link
that declaration to a definition at file scope (the namespace scope that
contains Friendly in this case). That definition appears after the
definition of the function h( ). The linking of the call to f( )
inside h( ) to the same function is a separate matter, however.
This is resolved by ADL. Since the argument of f( ) inside h( )
is a Friendly object, the Friendly class is searched for a
declaration of f( ), which succeeds. If the call were f(1)
instead (which makes some sense since 1 can be implicitly converted to Friendly(1)),
the call should fail, since there is no hint of where the compiler should look
for the declaration of f( ). The EDG compiler correctly complains
that f is undefined in that case.
Now suppose that Friendly and f are both
templates, as in the following program:
|
First notice that angle brackets in the declaration of f
inside Friendly. This is necessary to tell the compiler that f is
a template. Otherwise, the compiler will look for an ordinary function named f
and not find it. We could have inserted the template parameter (<T>)
in the brackets, but it is easily deduced from the declaration.
The forward declaration of the function template f
before the class definition is necessary, even though it wasn't in the previous
example when f was a not a template; the language specifies that friend
function templates must be previously declared. To properly declare f, Friendly
must also have been declared, since f takes a Friendly argument,
hence the forward declaration of Friendly in the beginning. We could
have placed the full definition of f right after the initial declaration
of Friendly instead of separating its definition and declaration, but we
chose instead to leave it in a form that more closely resembles the previous
example.
One last option remains for using friends inside templates:
fully define them inside the host class template definition itself. Here is how
the previous example would appear with that change:
|
There is an important difference between this and the
previous example: f is not a template here, but is an ordinary function.
(Remember that angle brackets were necessary before to imply that f( )
was a template.) Every time the Friendly class template is instantiated,
a new, ordinary function overload is created that takes an argument of the
current Friendly specialization. This is what Dan Saks has called
“making new friends.”(68) This
is the most convenient way to define friend functions for templates.
To clarify, suppose you want to add non-member friend
operators to a class template. Here is a class template that simply holds a
generic value:
|
Without understanding the previous examples in this section,
novices find themselves frustrated because they can't get a simple stream
output inserter to work. If you don't define your operators inside the
definition of Box, you must provide the forward declarations we showed
earlier:
|
Here we are defining both an addition operator and an output
stream operator. The main program reveals a disadvantage of this approach: you
can't depend on implicit conversions (the expression b1 + 2) because
templates do not provide them. Using the in-class, non-template approach is
shorter and more robust:
|
Because the operators are normal functions (overloaded for
each specialization of Box—just int in this case), implicit
conversions are applied as normal; so the expression b1 + 2 is valid.
Note that there's one type in particular that cannot be made
a friend of Box, or any other class template for that matter, and that
type is T—or rather, the type that the class template is parameterized
upon. To the best of our knowledge, there are really no good reasons why this
shouldn't be allowed, but as is, the declaration friend class T is
illegal, and should not compile.
Friend templates
You can be precise as to which specializations of a template
are friends of a class. In the examples in the previous section, only the
specialization of the function template f with the same type that
specialized Friendly was a friend. For example, only the specialization f<int>(const
Friendly<int>&) is a friend of the class Friendly<int>.
This was accomplished by using the template parameter for Friendly to
specialize f in its friend declaration. If we had wanted to, we could
have made a particular, fixed specialization of f a friend to all
instances of Friendly, like this:
|
By using double instead of T, the double
specialization of f has access to the non-public members of any Friendly
specialization. The specialization f<double>( ) still isn't
instantiated unless it is explicitly called.
Likewise, if you declare a non-template function with no
parameters dependent on T, that single function is a friend to all
instances of Friendly:
|
As always, since g(int) is unqualified, it must be
defined at file scope (the namespace scope containing Friendly).
It is also possible to arrange for all specializations of f
to be friends for all specializations of Friendly, with a so-called friend
template, as follows:
|
Since the template argument for the friend declaration is
independent of T, any combination of T and U is allowed,
achieving the friendship objective. Like member templates, friend templates can
appear within non-template classes as well.
2.3.5. Template programming idioms
Since language is a tool of thought, new language features
tend to spawn new programming techniques. In this section we cover some
commonly used template programming idioms that have emerged in the years since
templates were added to the C++ language.(69)
2.3.5.1. Traits
The traits template technique, pioneered by Nathan Myers, is a means of bundling type-dependent declarations together. In essence, using
traits you can “mix and match” certain types and values with contexts that use
them in a flexible manner, while keeping your code readable and maintainable.
The simplest example of a traits template is the numeric_limits class template defined in <limits>. The primary template is defined as follows:
|
The <limits> header defines specializations for
all fundamental, numeric types (when the member is_specialized is set to
true). To obtain the base for the double version of your floating-point
number system, for example, you can use the expression numeric_limits<double>::radix.
To find the smallest integer value available, you can use numeric_limits<int>::min( ).
Not all members of numeric_limits apply to all fundamental types. (For
example, epsilon( ) is only meaningful for floating-point types.)
The values that will always be integral are static data
members of numeric_limits. Those that may not be integral, such as the
minimum value for float, are implemented as static inline member
functions. This is because C++ allows only integral static data member
constants to be initialized inside a class definition.
In Chapter 3 you saw how traits are used to control the
character-processing functionality used by the string classes. The classes std::string
and std::wstring are specializations of the std::basic_string
template, which is defined as follows:
|
The template parameter charT represents the
underlying character type, which is usually either char or wchar_t.
The primary char_traits template is typically empty, and specializations
for char and wchar_t are provided by the standard library. Here
is the specification of the specialization char_traits<char>
according to the C++ Standard:
|
These functions are used by the basic_string class
template for character-based operations common to string processing. When you
declare a string variable, such as:
|
you are actually declaring s as follows (because of
the default template arguments in the specification of basic_string):
|
Because the character traits have been separated from the basic_string
class template, you can supply a custom traits class to replace std::char_traits.
The following example illustrates this flexibility:
|
|
In this program, instances of the guest classes Boy
and Bear are served items appropriate to their tastes. Boys like
milk and cookies, and Bears like condensed milk and honey. This
association of guests to items is done via specializations of a primary (empty)
traits class template. The default arguments to BearCorner ensure that
guests get their proper items, but you can override this by simply providing a
class that meets the requirements of the traits class, as we do with the MixedUpTraits
class above. The output of this program is:
|
Using traits provides two key advantages: (1) it allows
flexibility and extensibility in pairing objects with associated attributes or
functionality, and (2) it keeps template parameter lists small and readable. If
30 types were associated with a guest, it would be inconvenient to have to
specify all 30 arguments directly in each BearCorner declaration.
Factoring the types into a separate traits class simplifies things
considerably.
The traits technique is also used in implementing streams
and locales, as we showed in Chapter 4. An example of iterator traits is found
in the header file PrintSequence.h in Chapter 6.
2.3.5.2. Policies
If you inspect the char_traits specialization for wchar_t,
you'll see that it is practically identical to its char counterpart:
|
The only real difference between the two versions is the set
of types involved (char and int vs. wchar_t and wint_t).
The functionality provided is the same.(70) This
highlights the fact that traits classes are indeed for traits, and the
things that change between related traits classes are usually types and
constant values, or fixed algorithms that use type-related template parameters.
Traits classes tend to be templates themselves, since the types and constants
they contain are seen as characteristics of the primary template parameter(s) (for
example, char and wchar_t).
It is also useful to be able to associate functionality
with template arguments, so that client programmers can easily customize
behavior when they code. The following version of the BearCorner program,
for instance, supports different types of entertainment:
|
The Action template parameter in the BearCorner
class expects to have a static member function named doAction( ),
which is used in BearCorner<>::entertain( ). Users can choose
Feed or Stuff at will, both of which provide the required
function. Classes that encapsulate functionality in this way are referred to as
policy classes. The entertainment “policies” are provided above through Feed::doAction( )
and Stuff::doAction( ). These policy classes happen to be ordinary
classes, but they can be templates, and can be combined with inheritance to
great advantage. For more in-depth information on policy-based design, see
Andrei Alexandrescu's book,(71) the
definitive source on the subject.
2.3.5.3. The curiously recurring template pattern
Any novice C++ programmer can figure out how to modify a class to keep track of the number of objects of that class that currently exist. All
you have to do is to add static members, and modify constructor and destructor
logic, as follows:
|
All constructors of CountedClass increment the static
data member count, and the destructor decrements it. The static member
function getCount( ) yields the current number of objects.
It would be tedious to manually add these members every time
you wanted to add object counting to a class. The usual object-oriented device used
to repeat or share code is inheritance, which is only half a solution in this
case. Observe what happens when we collect the counting logic into a base
class.
|
All classes that derive from Counted share the same,
single static data member, so the number of objects is tracked collectively
across all classes in the Counted hierarchy. What is needed is a way to
automatically generate a different base class for each derived class.
This is accomplished by the curious template construct illustrated below:
|
Each derived class derives from a unique base class that is
determined by using itself (the derived class) as a template parameter! This
may seem like a circular definition, and it would be, had any base class
members used the template argument in a computation. Since no data members of Counted
are dependent on T, the size of Counted (which is zero!) is known
when the template is parsed. So it doesn't matter which argument is used to
instantiate Counted because the size is always the same. Any derivation
from an instance of Counted can be completed when it is parsed, and
there is no recursion. Since each base class is unique, it has its own static
data, thus constituting a handy technique for adding counting to any class
whatsoever. Jim Coplien was the first to mention this interesting derivation
idiom in print, which he cited in an article, entitled “Curiously Recurring
Template Patterns.” (72)
2.3.6. Template metaprogramming
In 1993 compilers were beginning to support simple template
constructs so that users could define generic containers and functions. About
the same time that the STL was being considered for adoption into Standard C++,
clever and surprising examples such as the following were passed around among
members of the C++ Standards Committee:(73)
|
That this program prints the correct value of 12! is
not alarming. What is alarming is that the computation is complete before the
program even runs!
When the compiler attempts to instantiate Factorial<12>,
it finds it must also instantiate Factorial<11>, which requires Factorial<10>,
and so on. Eventually the recursion ends with the specialization Factorial<1>,
and the computation unwinds. Eventually, Factorial<12>::val is
replaced by the integral constant 479001600, and compilation ends. Since all
the computation is done by the compiler, the values involved must be
compile-time constants, hence the use of enum. When the program runs,
the only work left to do is print that constant followed by a newline. To
convince yourself that a specialization of Factorial results in the
correct compile-time value, you could use it as an array dimension, such as:
|
2.3.6.1. Compile–time programming
So what was meant to be a convenient way to perform type
parameter substitution turned out to be a mechanism to support compile-time
programming. Such a program is called a template metaprogram
(since you're in effect “programming a program”), and it turns out that you can
do quite a lot with it. In fact, template metaprogramming is Turing complete because it supports selection (if-else) and looping (through recursion). Theoretically,
then, you can perform any computation with it.(74) The
factorial example above shows how to implement repetition: write a recursive
template and provide a stopping criterion via a specialization. The following
example shows how to compute Fibonacci numbers at compile time by the same
technique:
|
Fibonacci numbers are defined mathematically as:
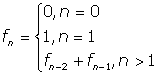
The first two cases lead to the template specializations
above, and the rule in the third line becomes the primary template.
Compile–time looping
To compute any loop in a template metaprogram, it must first
be reformulated recursively. For example, to raise the integer n to the
power p, instead of using a loop such as in the following lines:
|
you cast it as a recursive procedure:
|
This can now be easily rendered as a template metaprogram:
|
We need to use a partial specialization for the stopping
condition, since the value N is still a free template parameter. Note
that this program only works for non-negative powers.
The following metaprogram adapted from Czarnecki and Eisenecker(75) is interesting
in that it uses a template template parameter, and simulates passing a function
as a parameter to another function, which “loops through” the numbers 0..n:
|
The primary Accumulate template attempts to compute
the sum F(n)+F(n‑1)…F(0). The stopping criterion is obtained by a
partial specialization, which “returns” F(0). The parameter F is
itself a template, and acts like a function as in the previous examples in this
section. The templates Identity, Square, and Cube compute
the corresponding functions of their template parameter that their names
suggest. The first instantiation of Accumulate in main( )
computes the sum 4+3+2+1+0, because the Identity function simply
“returns” its template parameter. The second line in main( ) adds
the squares of those numbers (16+9+4+1+0), and the last computes the sum of the
cubes (64+27+8+1+0).
Loop unrolling
Algorithm designers have always endeavored to optimize their
programs. One time-honored optimization, especially for numeric programming, is
loop unrolling, a technique that minimizes loop overhead. The quintessential
loop-unrolling example is matrix multiplication. The following function
multiplies a matrix and a vector. (Assume that the constants ROWS and COLS
have been previously defined.):
|
If COLS is an even number, the overhead of
incrementing and comparing the loop control variable j can be cut in
half by “unrolling” the computation into pairs in the inner loop:
|
In general, if COLS is a factor of k, k
operations can be performed each time the inner loop iterates, greatly reducing
the overhead. The savings is only noticeable on large arrays, but that is
precisely the case with industrial-strength mathematical computations.
Function inlining also constitutes a form of loop unrolling.
Consider the following approach to computing powers of integers:
|
Conceptually, the compiler must generate three
specializations of power<>, one each for the template parameters
3, 2, and 1. Because the code for each of these functions can be inlined, the
actual code that is inserted into main( ) is the single expression m*m*m.
Thus, a simple template specialization coupled with inlining provides a way to
totally avoid loop control overhead.(76) This
approach to loop unrolling is limited by your compiler's inlining depth.
Compile–time selection
To simulate conditionals at compile time, you can use the
conditional ternary operator in an enum declaration. The following
program uses this technique to calculate the maximum of two integers at compile
time:
|
If you want to use compile-time conditions to govern custom
code generation, you can use specializations of the values true and false:
|
This program is equivalent to the expression:
|
except that the condition cond is evaluated at
compile time, and the appropriate versions of execute<>( ) and
Select<> are instantiatedby the compiler. The function Select<>::f( )
executes at runtime. A switch statement can be emulated in similar
fashion, but specializing on each case value instead of the values true
and false.
Compile–time assertions
In Chapter 2 we touted the virtues of using assertions as
part of an overall defensive programming strategy. An assertion is basically an
evaluation of a Boolean expression followed by a suitable action: do nothing if
the condition is true, or halt with a diagnostic message otherwise. It's best to
discover assertion failures as soon as possible. If you can evaluate an
expression at compile time, use a compile-time assertion. The following example
uses a technique that maps a Boolean expression to an array declaration:
|
The do loop creates a temporary scope for the
definition of an array, a, whose size is determined by the condition in
question. It is illegal to define an array of size -1, so when the condition is
false the statement should fail.
The previous section showed how to evaluate compile-time Boolean
expressions. The remaining challenge in emulating assertions at compile time is
to print a meaningful error message and halt. All that is required to halt the
compiler is a compile error; the trick is to insert helpful text in the error
message. The following example from Alexandrescu(77) uses template
specialization, a local class, and a little macro magic to do the job:
|
This example defines a function template, safe_cast<>( ),
that checks to see if the object it is casting from is no larger than the type
of object it casts to. If the size of the target object type is smaller, then
the user will be notified at compile time that a narrowing conversion was
attempted. Notice that the StaticCheck class template has the curious
feature that anything can be converted to an instance of StaticCheck<true>
(because of the ellipsis in its constructor(78)),
and nothing can be converted to a StaticCheck<false>
because no conversions are supplied for that specialization. The idea is to
attempt to create an instance of a new class and attempt to convert it to StaticCheck<true>
at compile time whenever the condition of interest is true, or to a StaticCheck<false>
object when the condition being tested is false. Since the sizeof
operator does its work at compile time, it is used to attempt the conversion.
If the condition is false, the compiler will complain that it doesn't know how
to convert from the new class type to StaticCheck<false>. (The
extra parentheses inside the sizeof invocation in STATIC_CHECK( )
are to prevent the compiler from thinking that we're trying to invoke sizeof
on a function, which is illegal.) To get some meaningful information inserted
into the error message, the new class name carries key text in its name.
The best way to understand this technique is to walk through
a specific case. Consider the line in main( ) above which reads:
|
The call to safe_cast<int>(p) contains the
following macro expansion replacing its first line of code:
|
(Recall that the token-pasting preprocessing operator, ##,
concatenates its operand into a single token, so Error_##NarrowingConversion
becomes the token Error_NarrowingConversion after preprocessing). The
class Error_NarrowingConversion is a local class (meaning that it
is declared inside a non-namespace scope) because it is not needed elsewhere in
the program. The application of the sizeof operator here attempts to
determine the size of an instance of StaticCheck<true> (because sizeof(void*)
<= sizeof(int) is true on our platforms), created implicitly from the
temporary object returned by the call Error_NarrowingConversion( ).
The compiler knows the size of the new class Error_NarrowingConversion (it's
empty), and so the compile-time use of sizeof at the outer level in STATIC_CHECK( )
is valid. Since the conversion from the Error_NarrowingConversion
temporary to StaticCheck<true> succeeds, so does this outer
application of sizeof, and execution continues.
Now consider what would happen if the comment were removed
from the last line of main( ):
|
Here the STATIC_CHECK( ) macro inside safe_cast<char>(p)
expands to:
|
Since the expression sizeof(void*) <= sizeof(char)
is false, a conversion from an Error_NarrowingConversion temporary to StaticCheck<false>
is attempted, as follows:
|
which fails, so the compiler halts with a message something
like the following:
|
The class name Error_NarrowingConversion is the
meaningful message judiciously arranged by the coder. In general, to perform a
static assertion with this technique, you just invoke the STATIC_CHECK
macro with the compile-time condition to check and with a meaningful name to
describe the error.
2.3.6.2. Expression templates
Perhaps the most powerful application of templates is a
technique discovered independently in 1994 by Todd Veldhuizen(79) and Daveed
Vandevoorde:(80) expression
templates. Expression templates enable extensive compile-time optimization
of certain computations that result in code that is at least as fast as
hand-optimized Fortran, and yet preserves the natural notation of mathematics
via operator overloading. Although you wouldn't be likely to use this technique
in everyday programming, it is the basis for a number of sophisticated,
high-performance mathematical libraries written in C++.(81)
To motivate the need for expression templates, consider typical
numerical linear algebra operations, such as adding together two matrices or
vectors,(82) such as in the
following:
|
In naive implementations, this expression would result in a
number of temporaries—one for A+B, and one for (A+B)+C. When
these variables represent immense matrices or vectors, the coincident drain on
resources is unacceptable. Expression templates allow you to use the same
expression without temporaries.
The following program defines a MyVector class to
simulate mathematical vectors of any size. We use a non-type template argument
for the length of the vector. We also define a MyVectorSum class to act
as a proxy class for a sum of MyVector objects. This allows us to use
lazy evaluation, so the addition of vector components is performed on demand
without the need for temporaries.
|
The MyVectorSum class does no computation when it is
created; it merely holds references to the two vectors to be added. Calculations
happen only when you access a component of a vector sum (see its operator[ ]( )).
The overload of the assignment operator for MyVector that takes a MyVectorSum
argument is for an expression such as:
|
When the expression v1+v2 is evaluated, a MyVectorSum
object is returned (or actually, inserted inline, since that operator+( )
is declared inline). This is a small, fixed-size object (it holds only
two references). Then the assignment operator mentioned above is invoked:
|
This assigns to each element of v3 the sum of the
corresponding elements of v1 and v2, computed in real time. No
temporary MyVector objects are created.
This program does not support an expression that has more
than two operands, however, such as
|
The reason is that, after the first addition, a second
addition is attempted:
|
which would require an operator+( ) with a first
argument of MyVectorSum and a second argument of type MyVector.
We could attempt to provide a number of overloads to meet all situations, but
it is better to let templates do the work, as in the following version of the
program:
|
The template facility deduces the argument types of a sum
using the template arguments, Left and Right, instead of
committing to those types ahead of time. The MyVectorSum template takes
these extra two parameters so it can represent a sum of any combination of
pairs of MyVector and MyVectorSum.
The assignment operator is now a member function template.
This allows any <T, N> pair to be coupled with any <Left,
Right> pair, so a MyVector object can be assigned from a MyVectorSum
holding references to any possible pair of the types MyVector and MyVectorSum.
As we did before, let's trace through a sample assignment to
understand exactly what takes place, beginning with the expression
|
Since the resulting expressions become quite unwieldy, in
the explanation that follows, we will use MVS as shorthand for MyVectorSum,
and will omit the template arguments.
The first operation is v1+v2, which invokes the
inline operator+( ), which in turn inserts MVS(v1, v2) into
the compilation stream. This is then added to v3, which results in a
temporary object according to the expression MVS(MVS(v1, v2), v3). The
final representation of the entire statement is
|
This transformation is all arranged by the compiler and
explains why this technique carries the moniker “expression templates.” The template
MyVectorSum represents an expression (an addition, in this case), and
the nested calls above are reminiscent of the parse tree of the left-associative
expression v1+v2+v3.
An excellent article by Angelika Langer and Klaus Kreft explains how this technique can be extended to more complex computations.(83)
2.3.7. Template compilation models
You may have noticed that all our template examples place
fully-defined templates within each compilation unit. (For example, we place
them completely within single-file programs, or in header files for multi-file
programs.) This runs counter to the conventional practice of separating ordinary
function definitions from their declarations by placing the latter in header
files and the function implementations in separate (that is, .cpp)
files.
The reasons for this traditional separation are:
- Non-inline function bodies in header files lead to multiple function definitions, resulting in linker errors.
- Hiding the implementation from clients helps reduce compile-time coupling.
- Vendors can distribute pre-compiled code (for a particular compiler) along with headers so that users cannot see the function implementations.
- Compile times are shorter since header files are smaller.
2.3.7.1. The inclusion model
Templates, on the other hand, are not code per se, but
instructions for code generation. Only template instantiations are real code.
When a compiler has seen a complete template definition during a compilation
and then encounters a point of instantiation for that template in the same
translation unit, it must deal with the fact that an equivalent point of
instantiation may be present in another translation unit. The most common
approach consists of generating the code for the instantiation in every
translation unit and letting the linker weed out duplicates. That particular
approach also works well with inline functions that cannot be inlined and with
virtual function tables, which is one of the reasons for its popularity. Nonetheless,
several compilers prefer instead to rely on more complex schemes to avoid
generating a particular instantiation more than once. Either way, it is the
responsibility of the C++ translation system to avoid errors due to multiple
equivalent points of instantiation.
A drawback of this approach is that all template source code
is visible to the client, so there is little opportunity for library vendors to
hide their implementation strategies. Another disadvantage of the inclusion
model is that header files are much larger than they would be if function
bodies were compiled separately. This can increase compile times dramatically
over traditional compilation models.
To help reduce the large headers required by the inclusion
model, C++ offers two (non-exclusive) alternative code organization mechanisms:
you can manually instantiate each specialization using explicit instantiation
or you can use exported templates, which support a large degree of
separate compilation.
2.3.7.2. Explicit instantiation
You can manually direct the compiler to instantiate any
template specializations of your choice. When you use this technique, there
must be one and only one such directive for each such specialization; otherwise
you might get multiple definition errors, just as you would with
ordinary, non-inline functions with identical signatures. To illustrate, we
first (erroneously) separate the declaration of the min( ) template
from earlier in this chapter from its definition, following the normal pattern
for ordinary, non-inline functions. The following example consists of five
files:
- OurMin.h: contains the declaration of the min( ) function template.
- OurMin.cpp: contains the definition of the min( ) function template.
- UseMin1.cpp: attempts to use an int-instantiation of min( ).
- UseMin2.cpp: attempts to use a double-instantiation of min( ).
- MinMain.cpp: calls usemin1( ) and usemin2( ).
|
|
|
|
|
When we attempt to build this program, the linker reports
unresolved external references for min<int>( ) and min<double>( ).
The reason is that when the compiler encounters the calls to specializations of
min( ) in UseMin1 and UseMin2, only the declaration
of min( ) is visible. Since the definition is not available, the
compiler assumes it will come from some other translation unit, and the needed
specializations are thus not instantiated at that point, leaving the linker to eventually
complain that it cannot find them.
To solve this problem, we will introduce a new file, MinInstances.cpp,
that explicitly instantiates the needed specializations of min( ):
|
To manually instantiate a particular template
specialization, you precede the specialization's declaration with the template
keyword. Note that we must include OurMin.cpp, not OurMin.h,
here, because the compiler needs the template definition to perform the
instantiation. This is the only place where we have to do this in this program,(84) however, since
it gives us the unique instantiations of min( ) that we need—the declarations
alone suffice for the other files. Since we are including OurMin.cpp
with the macro preprocessor, we add include guards:
|
Now when we compile all the files together into a complete
program, the unique instances of min( ) are found, and the program
executes correctly, giving the output:
|
You can also manually instantiate classes and static data
members. When explicitly instantiating a class, all member functions for the
requested specialization are instantiated, except any that may have been explicitly
instantiated previously. This is important, as it will render many templates
useless when using this mechanism—specifically, templates that implement
different functionality depending on their parameterization type. Implicit
instantiation has the advantage here: only member functions that get called are
instantiated.
Explicit instantiation is intended for large projects where
a hefty chunk of compilation time can be avoided. Whether you use implicit or
explicit instantiation is independent of which template compilation you use. You
can use manual instantiation with either the inclusion model or the separation
model (discussed in the next section).
2.3.7.3. The separation model
The separation model of template compilation separates function template definitions or static data member definitions from their
declarations across translation units, just like you do with ordinary functions
and data, by exporting templates. After reading the preceding two
sections, this must sound strange. Why bother to have the inclusion model in
the first place if you can just adhere to the status quo? The reasons are both
historical and technical.
Historically, the inclusion model was the first to experience
widespread commercial use—all C++ compilers support the inclusion model. Part
of the reason for that was that the separation model was not well specified
until late in the standardization process, but also that the inclusion model is
easier to implement. A lot of working code was in existence long before the
semantics of the separation model were finalized.
The separation model is so difficult to implement that, as
of Summer 2003, only one compiler front end (EDG) supports the separation
model, and at the moment it still requires that template source code be
available at compile time to perform instantiation on demand. Plans are in
place to use some form of intermediate code instead of requiring that the
original source be at hand, at which point you will be able to ship
“pre-compiled” templates without shipping source code. Because of the lookup
complexities explained earlier in this chapter (about dependent names being
looked up in the template definition context), a full template definition still
has to be available in some form when you compile a program that instantiates
it.
The syntax to separate the source code of a template
definition from its declaration is easy enough. You use the export keyword:
|
Similar to inline or virtual, the export
keyword need only be mentioned once in a compilation stream, where an exported
template is introduced. For this reason, we need not repeat it in the
implementation file, but it is considered good practice to do so:
|
The UseMin files used previously only need to include
the correct header file (OurMin2.h), and the main program doesn't
change. Although this appears to give true separation, the file with the
template definition (OurMin2.cpp) must still be shipped to users (because
it must be processed for each instantiation of min( )) until such
time as some form of intermediate code representation of template definitions
is supported. So while the standard does provide for a true separation model,
not all of its benefits can be reaped today. Only one family of compilers
currently supports export (those based on the EDG front end), and these
compilers currently do not exploit the potential ability to distribute template
definitions in compiled form.
2.3.8. Summary
Templates go far beyond simple type parameterization. When
you combine argument type deduction, custom specialization, and template
metaprogramming, C++ templates emerge as a powerful code generation mechanism.
One of the weaknesses of C++ templates that we did not
mention is the difficulty in interpreting compile-time error messages. The quantity
of inscrutable text spewed out by the compiler can be quite overwhelming. C++
compilers have improved their template error messages, and Leor Zolman has written a tool called STLFilt that renders these error messages much
more readable by extracting the useful information and throwing away the rest.(85)
Another important idea to take away from this chapter is
that a template implies an interface. That is, even though the template
keyword says “I'll take any type,” the code in a template definition requires
that certain operators and member functions be supported—that's the interface.
So in reality, a template definition is saying, “I'll take any type that
supports this interface.” Things would be much nicer if the compiler could
simply say, “Hey, this type that you're trying to instantiate the template with
doesn't support that interface—can't do it.” Using templates constitutes a sort
of “latent type checking” that is more flexible than the pure object-oriented
practice of requiring all types to derive from certain base classes.
In Chapters 6 and 7 we explore in depth the most famous
application of templates, the subset of the Standard C++ library commonly known
as the Standard Template Library (STL). Chapters 9 and 10 also use template
techniques not found in this chapter.
2.3.9. Exercises
Solutions
to selected exercises can be found in the electronic document The Thinking
in C++ Volume 2 Annotated Solution Guide, available for a small fee from www.MindView.net.
- Write a unary function template that takes a single type template parameter. Create a full specialization for the type int. Also create a non-template overload for this function that takes a single int parameter. Have your main program invoke three function variations.
- Write a class template that uses a vector to implement a stack data structure.
- Modify your solution to the previous exercise so that the type of the container used to implement the stack is a template template parameter.
- In the following code, the class NonComparable does not have an operator=( ). Why would the presence of the class HardLogic cause a compile error, but SoftLogic would not?
- Write a function template that takes a single type parameter (T) and accepts four function arguments: an array of T, a start index, a stop index (inclusive), and an optional initial value. The function returns the sum of all the array elements in the specified range and the initial value. Use the default constructor of T for the default initial value.
- Repeat the previous exercise but use explicit instantiation to manually create specializations for int and double, following the technique explained in this chapter.
- Why does the following code not compile? (Hint: what do class member functions have access to?)
- Why does the following code not compile?
- Write templates that take non-type parameters of the following variety: an int, a pointer to an int, a pointer to a static class member of type int, and a pointer to a static member function.
- Write a class template that takes two type parameters. Define a partial specialization for the first parameter, and another partial specialization that specifies the second parameter. In each specialization, introduce members that are not in the primary template.
- Define a class template named Bob that takes a single type parameter. Make Bob a friend of all instances of a template class named Friendly, and a friend of a class template named Picky only when the type parameter of Bob and Picky are identical. Give Bob member functions that demonstrate its friendship.
|
|
|
| (51) | Vandevoorde and Josuttis, C++ Templates: The Complete Guide, Addison Wesley, 2003. Note that “Daveed” sometimes appears as “David.” |
| (52) | The C++ Standards Committee is considering relaxing the only–within–a–template rule for these disambiguation hints, and some compilers allow them in non–template code already. |
| (53) | See Stroustrup, The C++ Programming Language, 3rd Edition, Addison Wesley, pp. 335–336. |
| (54) | Technically, comparing two pointers that are not inside the same array is undefined behavior, but today's compilers don't complain about this. All the more reason to do it right. |
| (55) | We are indebted to Nathan Myers for this example. |
| (56) | Such as type information encoded in a decorated name. |
| (57) | C++ compilers can introduce names anywhere they want, however. Fortunately, most don't declare names they don't need. |
| (58) | If you're interested in seeing the proposal, it's Core Issue 352. |
| (59) | A reference to the British animated short films by Nick Park featuring Wallace and Gromit. |
| (60) | We discuss vector<bool> in depth in Chapter 7. |
| (61) | Instead of this–> you could use any valid qualification, such as Sortable::at( ) or vector<T>::at( ). The point is that it must be qualified. |
| (62) | See also the explanation accompanying PriorityQueue6.cpp in Chapter 7. |
| (63) | Since the forwarding functions are inline, no code for Stack<void*> is generated at all! |
| (64) | Also called Koenig lookup, after Andrew Koenig, who first proposed the technique to the C++ Standards Committee. ADL applies universally, whether templates are involved or not. |
| (65) | From a presentation by Herb Sutter. |
| (66) | A number of compilers use this front end, including Comeau C++. |
| (67) | Also based on an example by Herb Sutter. |
| (68) | In a talk given at The C++ Seminar, Portland, OR, September, 2001. |
| (69) | Another template idiom, mixin inheritance, is covered in Chapter 9. |
| (70) | The fact that char_traits<>::compare( ) may call strcmp( ) in one instance vs. wcscmp( ) in another, for example, is immaterial to the point we make here: the “function” performed by compare( ) is the same. |
| (71) | Modern C++ Design: Generic Programming and Design Patterns Applied, Addison Wesley, 2001. |
| (72) | C++ Gems, edited by Stan Lippman, SIGS, 1996. |
| (73) | These are technically compile–time constants, so you could argue that the identifiers should be all uppercase letters to follow the usual form. We left them lowercased because they are simulations of variables. |
| (74) | In 1966 Böhm and Jacopini proved that any language supporting selection and repetition, along with the ability to use an arbitrary number of variables, is equivalent to a Turing machine, which is believed capable of expressing any algorithm. |
| (75) | Czarnecki and Eisenecker, Generative Programming: Methods, Tools, and Applications, Addison Wesley, 2000, p. 417. |
| (76) | There is a much better way to compute powers of integers: the Russian Peasant Algorithm. |
| (77) | Modern C++ Design, pp. 23–26. |
| (78) | You are not allowed to pass object types (other than built–ins) to an ellipsis parameter specification, but since we are only asking for its size (a compile–time operation), the expression is never actually evaluated at runtime. |
| (79) | A reprint of Todd's original article can be found in Lippman, C++ Gems, SIGS, 1996. It should also be noted that besides retaining mathematical notation and optimized code, expression templates also allow for C++ libraries to incorporate paradigms and mechanisms found in other programming languages, such as lambda expressions. Another example is the fantastic class library Spirit, which is a parser that makes heavy use of expression templates, allowing for (an approximate) EBNF notation directly in C++, resulting in extremely efficient parsers. Visit http://spirit.sourceforge.net/. |
| (80) | See his and Nico's book, C++ Templates, book cited earlier. |
| (81) | Namely, Blitz++ (http://www.oonumerics.org/blitz/), the Matrix Template Library (http://www.osl.iu.edu/research/mtl/), and POOMA (http://www.acl.lanl.gov/pooma/). |
| (82) | We mean “vector” in the mathematical sense, as a fixed–length, one–dimensional, numerical array. |
| (83) | Langer and Kreft, “C++ Expression Templates,” C/C++ Users Journal, March 2003. See also the article on expression templates by Thomas Becker in the June 2003 issue of the same journal (that article was the inspiration for the material in this section). |
| (84) | As explained earlier, you must explicitly instantiate a template only once per program. |
| (85) | Visit http://www.bdsoft.com/tools/stlfilt.html. |